[数据结构与算法] 猿创征文 | 详解二叉树之遍历及其应用（动图遍历演示）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 猿创征文 | 详解二叉树之遍历及其应用（动图遍历演示） -> 正文阅读

[数据结构与算法]猿创征文 | 详解二叉树之遍历及其应用（动图遍历演示）

文章目录

?🌙知识回顾

大家好啊！💖💖💖我是vince，我们继续进入纯C实现数据结构的坑里来，上一篇文章 vince 详解了二叉树的顺序结构堆，详解了堆的概念、堆的实现、以及再实现时候用到的相关算法和堆的应用~

vnce今天给大家带来二叉树的遍历及其应用（也是二叉树的链式结构），这里的学习遍历是为了后面二叉树的应用打基础，在二叉树的很多应用甚至是很多面试题目中二叉树的那些遍历是必不可少的，因此这篇内容很是重要，??希望我在总结之余，也能给大家带来帮助。

当然在大家看这篇文章之前，vince 还是建议大家先复习复习前面的树的概念和结构以及堆，在向前学习的同时仍不忘回顾，毕竟子曰：温故而知新，可以为师矣。

👇👇👇
💘💘💘知识连线时刻（直接点击即可）

??🎉🎉🎉复习回顾🎉🎉🎉
???详解树的概念和结构
????详解二叉树之堆

我们首先来看看今天学习的思维导图：（主要是第二板块链式结构和遍历）
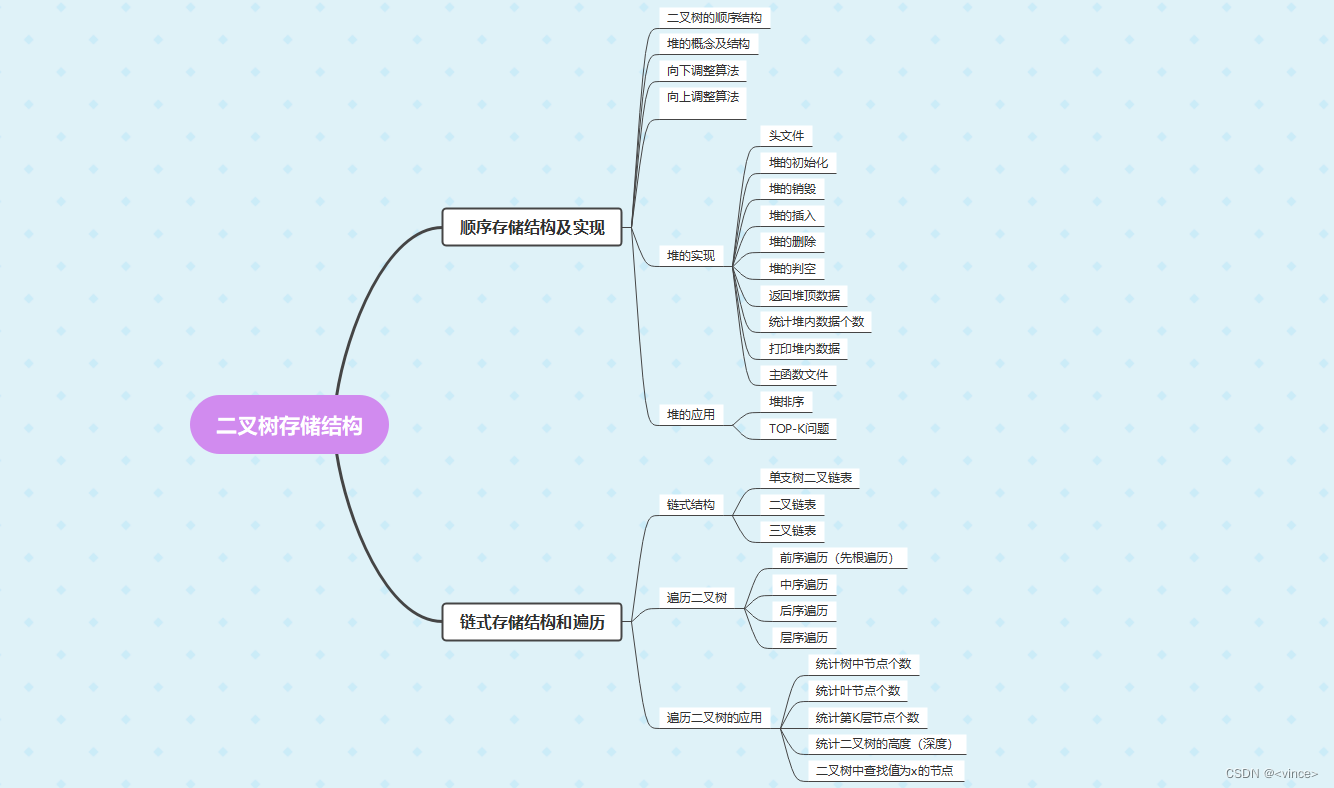
在这里插入图片描述

? 🍋知识点一：二叉树的链式存储结构

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链，当前我们介绍学习一般都是二叉链，后面学到高阶数据结构如红黑树等会用到三叉链。
图解分析：
在这里插入图片描述

? 🌰1. 二叉链表

二叉链代码示例：

typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
    struct BinTreeNode* _pLeft; // 指向当前节点左孩子
    struct BinTreeNode* _pRight; // 指向当前节点右孩子
    BTDataType _data; // 当前节点值域
}

二叉链图解分析：
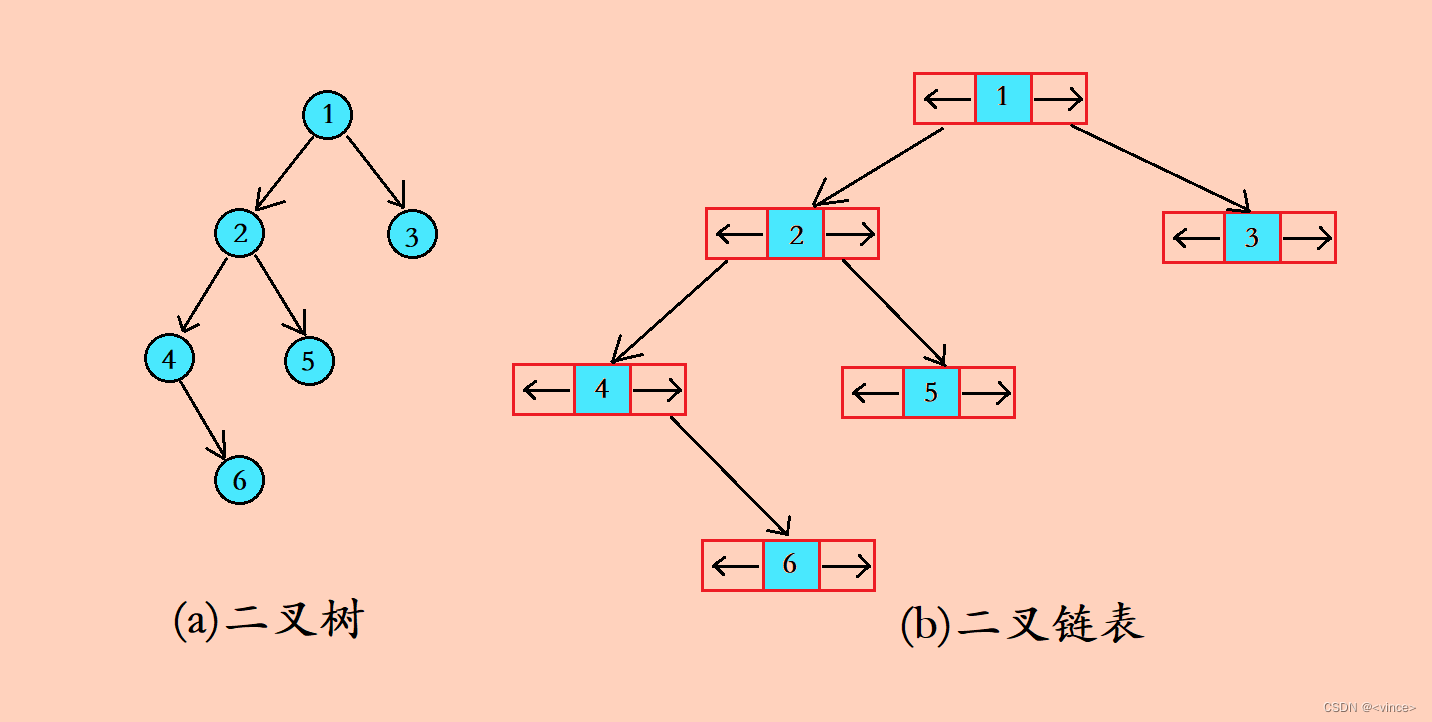
在这里插入图片描述

? 🌰2. 三叉链表

三叉链代码示例：

typedef int BTDataType;
// 三叉链
struct BinaryTreeNode
{
    struct BinTreeNode* _pParent; // 指向当前节点的双亲
    struct BinTreeNode* _pLeft; // 指向当前节点左孩子
    struct BinTreeNode* _pRight; // 指向当前节点右孩子
    BTDataType _data; // 当前节点值域
}；

三叉链图解分析：
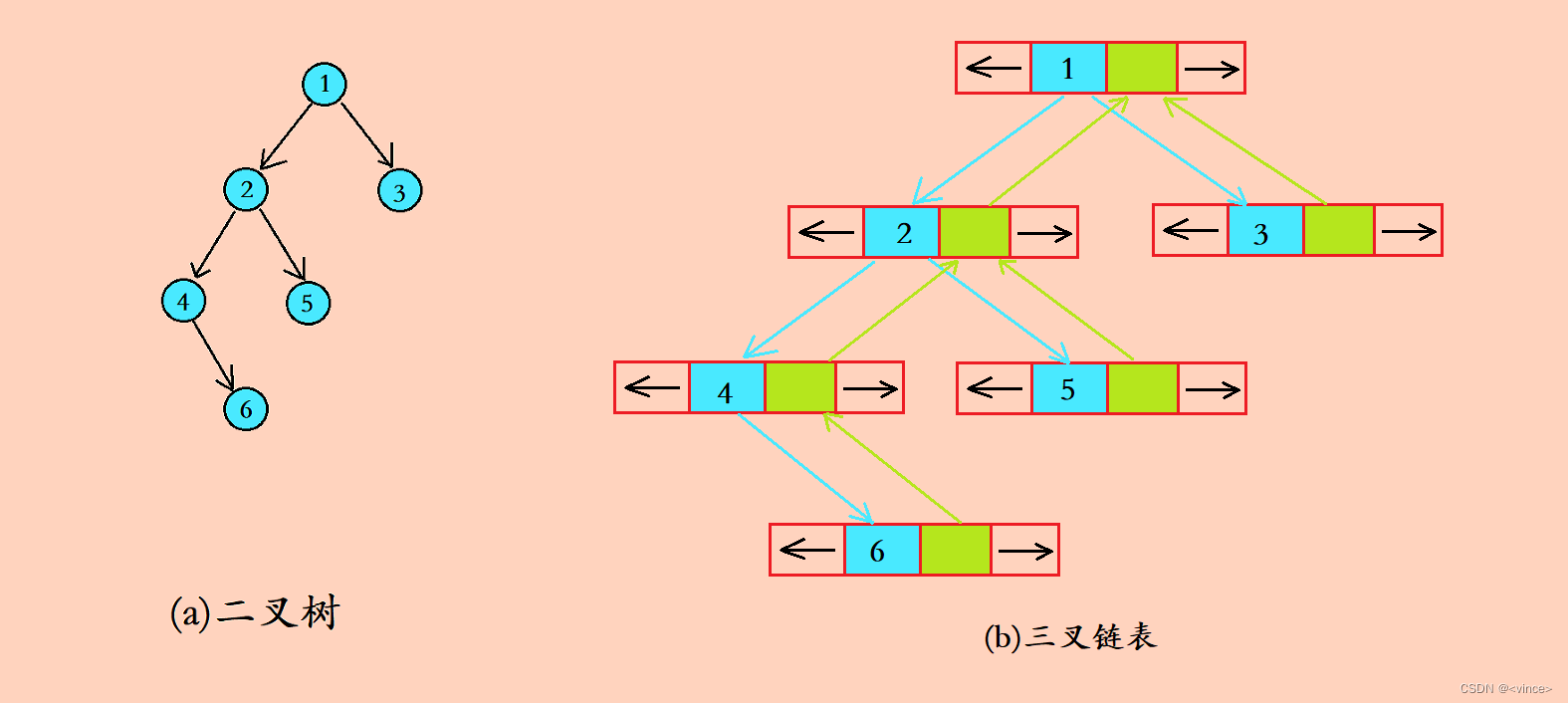
在这里插入图片描述

? 🍋知识点二：二叉树的遍历

以下遍历都以此二叉树为例：
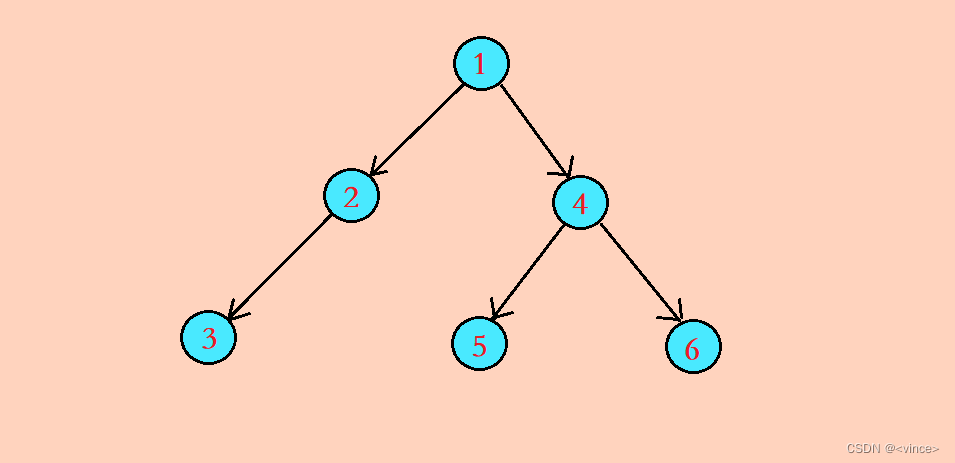
在这里插入图片描述

? 🌰1. 前序遍历

前序遍历也叫先根遍历。遍历规则：根，左，右

前序遍历动图展示：
在这里插入图片描述

以上树的遍历顺序为：1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
遍历结果：1 2 3 4 5 6

代码实现：

//前序遍历
void PrevOrder(BTNode* root)
{
    if (root == NULL)
    {
    	printf("NULL  ");
    	return;
    }
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

? 🌰2. 中序遍历

遍历规则：左，根，右

中序遍历动图展示：
在这里插入图片描述

以上树的遍历顺序为：NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
遍历结果：3 2 1 5 4 6

代码实现：

//中序遍历
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
    	printf("NULL  ");
    	return;
    }
    InOrder(root->left);
	printf("%d  ", root->data);
	InOrder(root->right);
}

? 🌰3. 后序遍历

遍历规则：左，右，根

后序遍历动图展示：
在这里插入图片描述

以上树的遍历顺序为：NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
遍历结果：3 2 5 6 4 1

代码实现：

//后序遍历
void PostOrder(BTNode* root)
{
    	if (root == NULL)
    	{
    		printf("NULL  ");
    		return;
    	}
    	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d  ", root->data);
}

? 🌰4. 层序遍历

遍历规则：一层一层的遍历

层序遍历动图展示：
在这里插入图片描述

以上树的遍历顺序为：1 2 4 3 NULL 5 6
遍历结果：1 2 4 3 5 6

代码实现：

//层序遍历
void LevelOrder(BTNode* root)
{
    Queue q;
    QueueInit(&q);//队列初始化，注意别忘记
    if (root)
    {
    	QueuePush(&q, root);//节点入队列
    }
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);//获取头节点
		QueuePop(&q);//每获取到头节点之后，就出队列

		printf("%d ", front->data);//将头节点的数据打印出来
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestory(&q);
}

在这里插入图片描述

? 🍋知识点三：二叉树遍历的应用

以下应用也都以此二叉树为例：
在这里插入图片描述

? 🌰1. 统计树中节点个数（思想：遍历+计数）

这个需要对树进行遍历统计，三种遍历方法都可以使用。这里依然存在一个细节问题需要注意，就是统计二叉树节点个数的变量使用细节。下面给三种不同的情况看看对比分析分析：
对比方法一：这里利用全局变量的传值调用操作
代码实现：

int count = 0;//定义全局变量
void BTreeSize(BTNode* root)
{
    if (root == NULL)
    {
    	return;
    }

    ++count;//放在这里是先序遍历
	BTreeSize(root->left);
 	//++count;放在这里是中序遍历
	BTreeSize(root->right);
    //++count;放在这里是后序遍历
}

运行结果示例：
在这里插入图片描述

💯文字分析：
第一点这里使用的先序遍历，当然其他遍历也可以使用；第二点就是全局变量存在的问题。因为这里无论全面遍历还是这里统计节点个数时使用的遍历都是利用递归算法思想实现的，而使用全部变量，在递归中变量会持续叠加，无法释放清除，所以当你调用这个函数多次，统计得到的节点数就依次叠加，从而出现统计结果不同。

对比方法二：这里利用定义静态变量来操作
首先说说为什么用静态局部变量？因为一个局部变量的作用域就在这个函数内部，出了函数就会销毁清除，而递归有需要不断的将函数递归出去，所以如果单纯使用局部的话，每次递归进入一个函数就会创建一个局部变量，每次都如此，这洋最初的局部变量就起不到统计叠加的效果。而弊端效果实际上和上面全局变量一样。
代码展示：

int BTreeSize(BTNode* root)
{
    static int count = 0;//利用静态局部变量来统计 
     //局部静态变量，只有第一次进来时执行这句话，所以对后面的每一次递归无影响
    if (root == NULL)
    {
    	return;
    }
    count++;//这里依然可以交换位置，拿三种遍历来实现
	BTreeSize(root->left);
	BTreeSize(root->right);
	return count;
}

运行实例结果：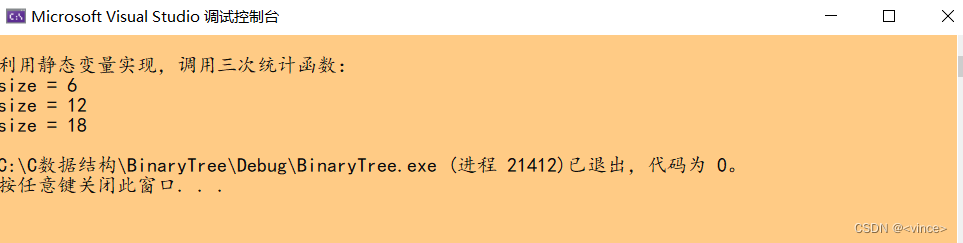
💯文字分析：
这里使用静态局部变量，存在统计持续叠加问题和上面全局变量的传值调用操作存在一样的问题。

那么问题来啦？以上两种我们最常见的变量使用方法在这里使用的时候都存在bug，不适合这里，我们应该怎么优化呢？

此时，我们思考思考递归的本质，想想递归的思想过程，我们发现递归实际上是：先递出去，再回归。既然我们的全局变量和静态变量无法进行清除，那我们可以直接定义一个局部变量然后传递局部变量的地址，后续统计节点的时候直接在局部变量的地址上就进行操作了，然后再整体都递归结束时，因为是局部变量嘛，出了作用域就自动清楚啦！以下就是优化后的代码~

对比方法三：优化后利用全部变量传址调用操作：
代码实现：

void BTreeSize(BTNode* root,int* pCount)
{
    if (root == NULL)
    {
    	return;
    }

    ++(*pCount);//这里就直接利用其指针进行叠加
	BTreeSize(root->left,pCount);
	BTreeSize(root->right,pCount);
}

//主函数相关处理
int main()
{
	BTNode* tree = CreatBinaryTree();
   //这种方法其实就是用一个变量，就传一个变量
	int count1 = 0;
	BTreeSize(tree,&count1);
	printf("size = %d\n", count1);
	int count2 = 0;
	BTreeSize(tree, &count2);
	printf("size = %d\n", count2);

	return 0;
}

运行结果示例：
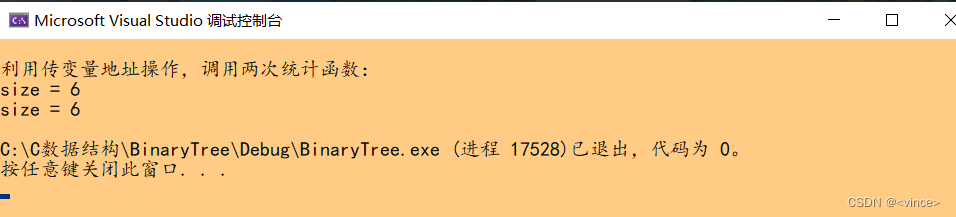
在这里插入图片描述
💯文字分析：
这优化以后就完全规避以上存在的问题，然后这里实现全局变量的灵活使用，在主函数里面想要使用时就定义，然后传递其地址进行操作，保证了技术安全。

方法对比四：利用子问题来操作
分治思想：把复杂的问题分成小规模的问题；把小规模的问题分成更小规模的问题，最终分到不能再分，直接得出结果。
思路一：若为空树，就是最小规模的子问题，节点数为零；
思路二：若不为空树，节点数为左子树节点数+右子树节点数+1，这里的1指的是最大的根。
代码实现：

int BTreeSize(BTNode* root)
{
    return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
}

💯文字分析：
递归其实就是一种分治算法思想，将其拆分拆分再拆分，最终直接统计节点个数。

? 🌰2. 统计树中叶子节点个数

这里依然和上面一样有两种思路：一：遍历+计数；二：分治。这里我们使用分治思想实现。
代码实现：

//统计叶节点个数（遍历+计数的思想）
int BTreeLeafSize(BTNode* root)
{
    if (root == NULL)
    {
    	return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
		return 1;
	}
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}

运行结果示例：
在这里插入图片描述

? 🌰3. 统计第K层节点个数（K>=1）

分治思想：
一：若为空树，返回0；
二：若非空，K == 1，返回1；
三：若非空，K>1，转换成左子树K-1层节点个数+右子树K-1层节点个数。
代码实现：

//统计第K层节点数
int BTreeKLevelSize(BTNode* root, int k)
{
    assert(k >= 1);
    if (root == NULL)
    {
    	return 0;
    }
    if (k == 1)
	{
		return 1;
	}

	return BTreeKLevelSize(root->left, k - 1) + BTreeKLevelSize(root->right, k - 1);
}

运行结果示例：
在这里插入图片描述

? 🌰4. 统计二叉树的高度（深度）

分治思想：
分别左子树高度和右子树高度，然后进行比较，两者之间较大的那个加一。
代码实现：

//统计二叉树的深度
int BTreeDepth(BTNode* root)
{
    	if (root == NULL)
    	{
    		return 0;
    	}

    	int leftdepth = BTreeDepth(root->left);//遍历统计左子树的深度
	int rightdepth = BTreeDepth(root->right);//遍历统计右子树的深度

	return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
}

运行结果示例：
在这里插入图片描述

? 🌰5. 二叉树中查找值为x的节点

代码实现：

//二叉树查找值为x的节点
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
    if (root == NULL)
    {
    	return NULL;
    }
    if (root->data == x)//（前序遍历）
    {
		return root;
	}
	BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1)
	{
		return ret1;
	}
	BTNode* ret2 = BTreeFind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
	return NULL;
}

运行结果示例：
在这里插入图片描述

? 🌰6. 二叉树的销毁（后序遍历销毁）

二叉树的销毁这里存在两种处理方法：一是传递一级指针来实现；二是传递二级指针来实现。
法一：（一级指针）
一级指针注意，在free之后需要注意此时在该作用域中置空无效，为防止后续放生冲突，需要再回到主函数时进行手动置空操作。
代码实现：

void BTreeDestroy(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

    BTreeDestroy(root->left);
    BTreeDestroy(root->right);
	free(root);
    //root = NULL;这里置空无效果，所以将置空放到主函数里面（因为这里传递的是一级指针）
}

//主函数调用
int main()
{
	BTNode* tree = CreatBinaryTree();
	BTreeDestroy(tree);
	tree = NULL;//因为一级指针在那边函数里面置空后出了作用域就无效，所以需要在这里再手动置空
	return 0;
}

法二：（二级指针）
二级指针实现时，后续就不需要再进行手动置空。

//传二级指针销毁二叉树
void BTreeDestroy(BTNode** pproot)
{
    if ((*pproot) == NULL)
    {
    	return;
    }

    BTreeDestroy(&(*pproot)->left);//注意因为是二级指针接收，这里需要传其节点指针的地址
	BTreeDestroy(&(*pproot)->right);
	free(*pproot);
	*pproot = NULL;//每次释放一个节点后就将其置空，因为这里传的是二级指针，可以直接操作有效
}
int main()
{
	BTNode* tree = CreatBinaryTree();
	BTreeDestroy(&tree);
 //传的二级指针，这里就不用在对tree手动置空了，因为在子函数运行完就自动置空了。
	return 0;
}

在这里插入图片描述

?🌙vince 结语

二叉树的遍历和相关应用的介绍和学习到这里就结束啦~目前简单的一些数据结构基本就拿C实现介绍差不多啦，后面就会进入排序的学习哈。但是在这里，希望大家能够将前面的树的基础概念以及之前的线性结构知识进行回顾复习，使整个纯C数据结构学习是连贯的，这样更加利于我们的学习和理解以及继续拓展。

如果各位大佬们觉得有一定帮助的话，就来个赞和收藏吧，如有不足之处也请批评指正。

代码不负有心人，98加满，向前冲啊🐬

在这里插入图片描述
🎉🎉🎉以上代码均可运行，所用编译环境为 vs2019 ,运行时注意加上编译头文件#define _CRT_SECURE_NO_WARNINGS 1