链接:https://leetcode.cn/problems/non-overlapping-intervals/solution/-by-xun-ge-v-tugq/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。?
题目
?
示例
?
思路
解题思路
【贪心】
需要移除区间的最小数量,使剩余区间互不重叠 。
那我们可以对区间左边界或者右边界进行排序,每次我们的先从最小区间开始选择,这样就可以获得更多的区间个数
- 按照右边界排序,就要从左向右遍历,因为右边界越小越好,只要右边界越小,留给下一个区间的空间就越大,所以从左向右遍历,优先选右边界小的。
- 按照左边界排序,就要从右向左遍历,因为左边界数值越大越好(越靠右),这样就给前一个区间的空间就越大,所以可以从右向左遍历。
如果按照左边界排序,还从左向右遍历的话,其实也可以,逻辑会有所不同。
一些同学做这道题目可能真的去模拟去重复区间的行为,这是比较麻烦的,还要去删除区间。
题目只是要求移除区间的个数,没有必要去真实的模拟删除区间!
我来按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
此时问题就是要求非交叉区间的最大个数。
右边界排序之后,局部最优:优先选右边界小的区间,所以从左向右遍历,留给下一个区间的空间大一些,从而尽量避免交叉。全局最优:选取最多的非交叉区间。
局部最优推出全局最优,试试贪心!
这里记录非交叉区间的个数还是有技巧的,如图:
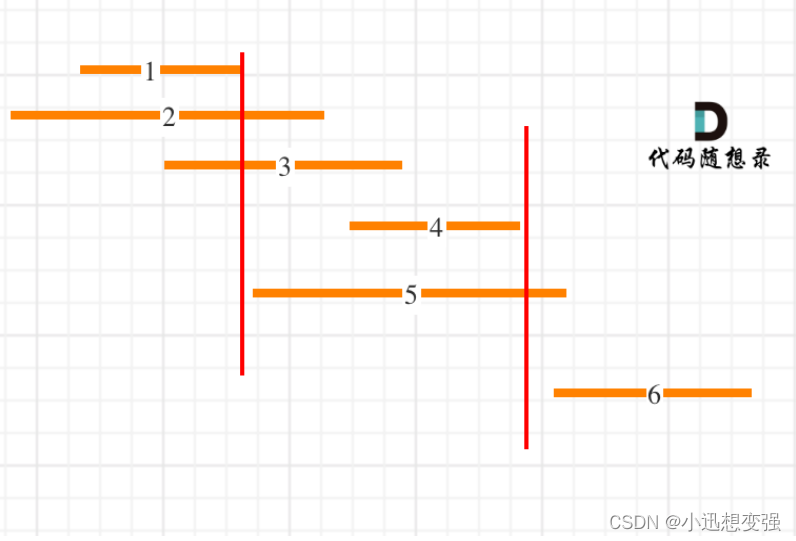
有人就会想遇见没有重叠的区间就将切割点换了,比如说上面如果 5 区间的左边界比较长,那对于第一个切割点来说也是覆盖呀,会不会出现问题呢?肯定是不会的,因为5区间如果左边界比较长那么肯定会覆盖到下一个切割点,也是会被删了的,只是删的时间不同而已
代码
int cmp(const void * a, const void * b)//排序
{
int * _a = *(int **)a;
int * _b = *(int **)b;
return _a[1] == _b[1] ? _a[0] - _b[0] : _a[1] - _b[1];
}
int eraseOverlapIntervals(int** intervals, int intervalsSize, int* intervalsColSize){
qsort(intervals, intervalsSize, sizeof(int *), cmp);//排序
int del = 0;//需要删除的区间个数
int res = intervals[0][1];//初始化起始位置
for(int i = 1; i < intervalsSize; i++)
{
if(res > intervals[i][0]) del++;//大于当前区间的左边,说明覆盖了,删了这个覆盖的
else res = intervals[i][1];//小于当前区间的左边,说明没有覆盖,更新初始化位置
}
return del;
}
作者:xun-ge-v
链接:https://leetcode.cn/problems/non-overlapping-intervals/solution/-by-xun-ge-v-tugq/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。