1.计数排序
计数排序是刷题常用的一种算法。但事实上我们并不把它用来排序,更多的是用来统计。实现这个算法需要两个数组,我们来看图具体分析:

这就是计数排序的基本思想——映射。即将arr的数组元素的值看成tmp数组的下标,然后统计arr数组中各个元素出现的次数,这也是为什么将此排序称为计数排序的原因。那么图中介绍的方式称为绝对映射。但是我们需要考虑一个问题,如果arr数组的元素依次为:1、2022、4312、99837,那么tmp的所开辟的空间必须以最大值为准,空间的浪费是非常严重的。

我们有一种新的概念叫做相对映射,可以一定程度上优化绝对映射带来的负面效果。我们看图:

此时我们便可以使用代码描述这个排序算法了:
#include <stdlib.h>
#include <assert.h>
#include <time.h>
#include <string.h>
#include <stdio.h>
void Print(int* a, int n)
{
assert(a);
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
}
void CountSort(int* a, int n)
{
assert(a);
//找到数组最大、最小的元素
int max = 0, min = a[0];
for (int i = 0; i < n; i++)
{
if (max < a[i])
{
max = a[i];
}
if (min > a[i])
{
min = a[i];
}
}
//创建tmp数组,并且进行映射
int size = max - min + 1;
int* tmp = (int*)calloc(1,sizeof(int) * size);
assert(tmp);
for (int i = 0; i < n; i++)
{
tmp[a[i] - min]++;
}
//将tmp的有效下标拷贝回arr数组
int count = 0;
for (int i = 0; i < size; i++)
{
while (tmp[i] != 0)
{
a[count++] = i;
tmp[i]--;
}
}
}
int main()
{
int size = 10;
int* arr = (int*)malloc(sizeof(int) * size);
assert(arr);
srand((unsigned int)time(NULL));
for (int i = 0; i < size; i++)
{
arr[i] = rand() % 100;
}
CountSort(arr, size);
Print(arr, size);
free(arr);
arr = NULL;
return 0;
}
观察代码可以发现,计数排序适合工作在非浮点数、且数值相对集中的场景中。

2.归并排序基本思想
假设我们有两个有序数组,我们的任务是将它合并成一个有序数组,我们应该如何操作?这就是归并排序的经典问题。
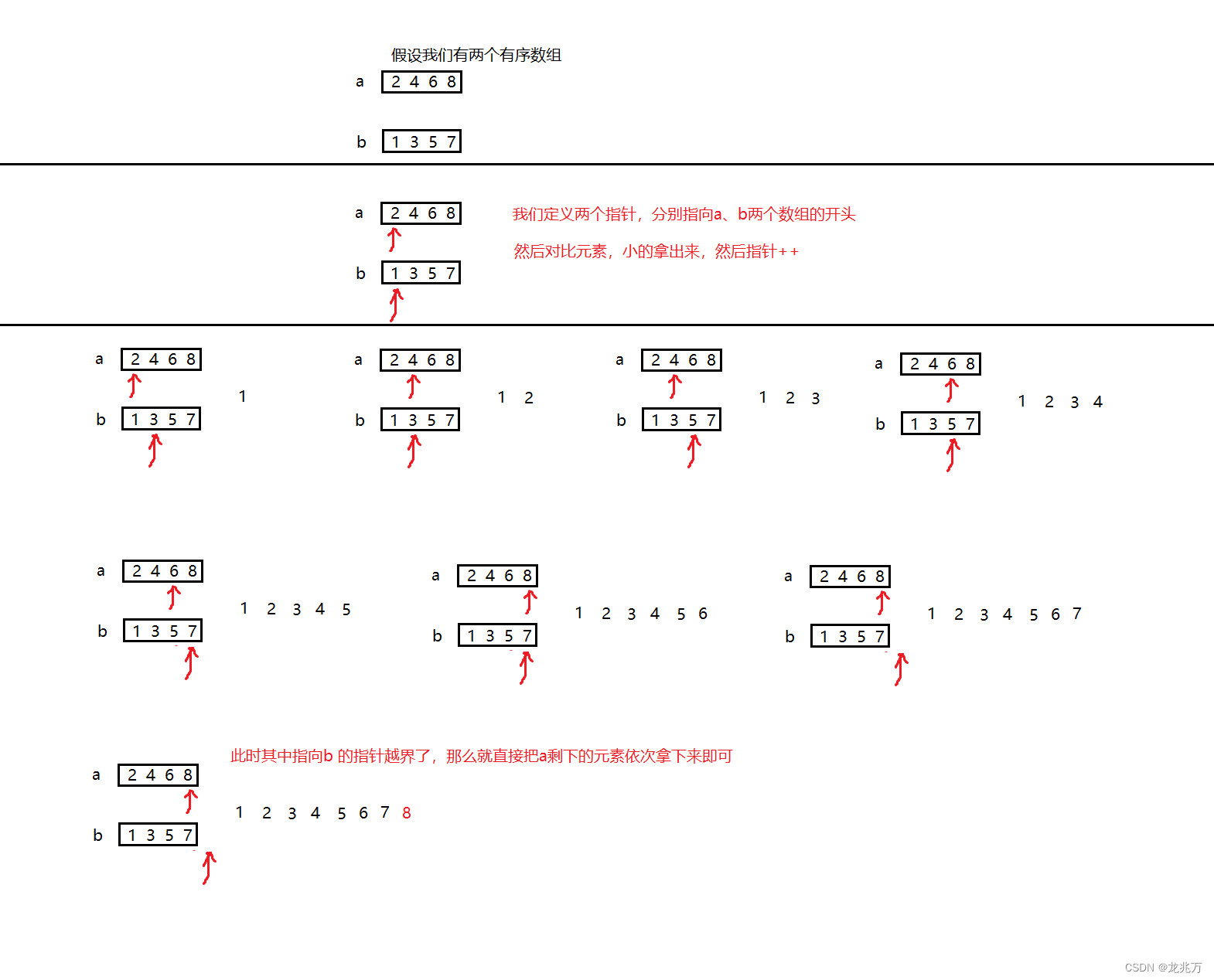
但是既然是排序算法,我们不可能每次都碰到两个有序数组让我们使用的。所以针对一个数组的时候,我们也可以将它拆为二叉树的结构去进行计算。
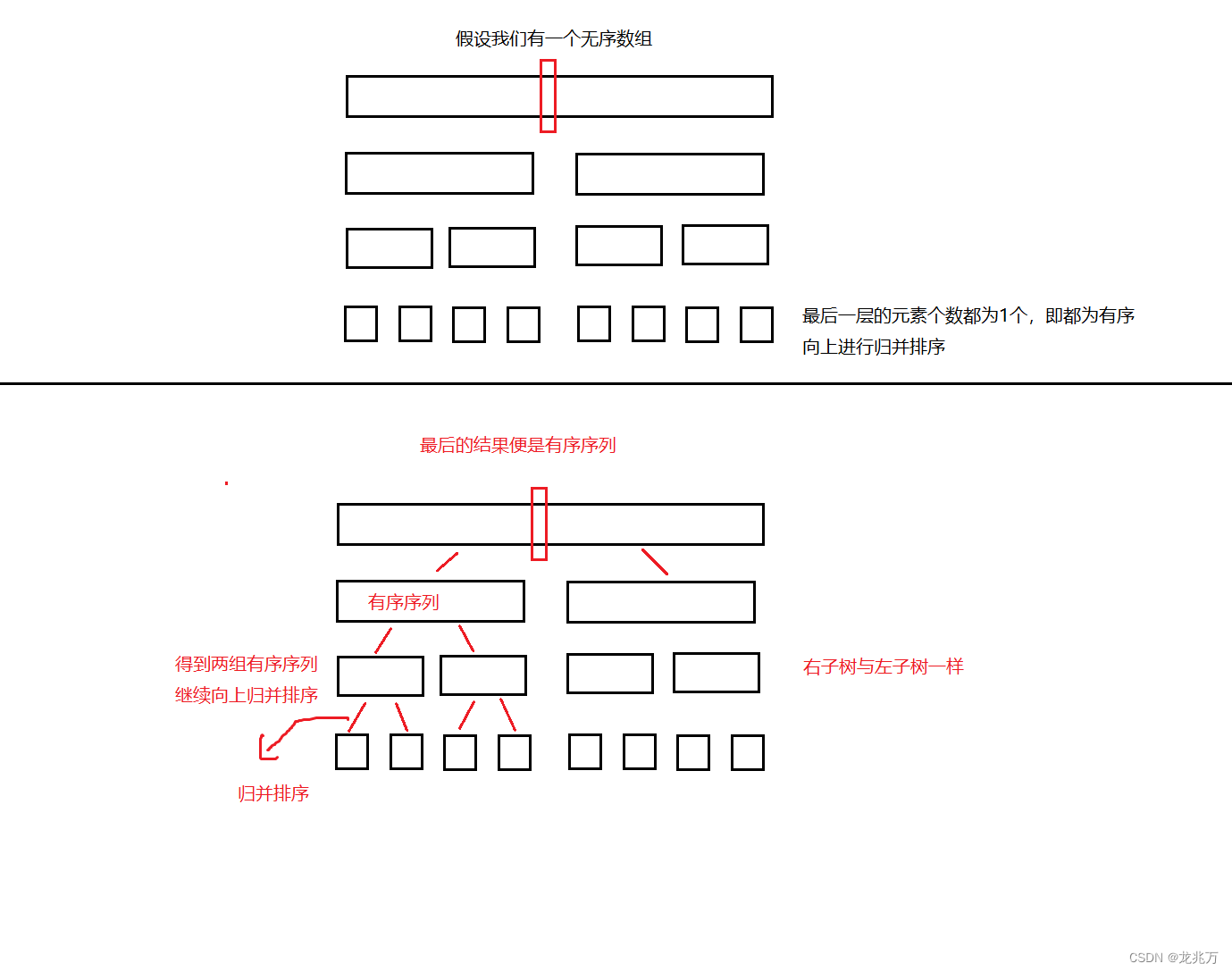
3.递归归并排序
使用递归更加契合二叉树结构。
void _MergeSort(int* a, int begin, int end, int* tmp)
{
assert(a && tmp);
//递归返回条件
if (begin >= end)
{
return;
}
//递归知道元素个数为1
int mid = (end + begin) / 2;
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid+1,end, tmp);
//开始归并排序
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
assert(a);
//归并需要一块空间存储有序序列
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
int main()
{
int size = 1000000;
int* arr = (int*)malloc(sizeof(int) * size);
assert(arr);
srand((unsigned int)time(NULL));
for (int i = 0; i < size; i++)
{
arr[i] = rand();
}
//CountSort(arr, size);
MergeSort(arr, size);
Print(arr, size);
free(arr);
arr = NULL;
return 0;
}
归并排序的时间复杂度为O(NlogN)*,效率也非常高,只不过空间复杂度稍微高一些。
4.非递归归并排序
非递归的归并排序可以看成是一颗倒的二叉树结构。与希尔排序可能有些相像。
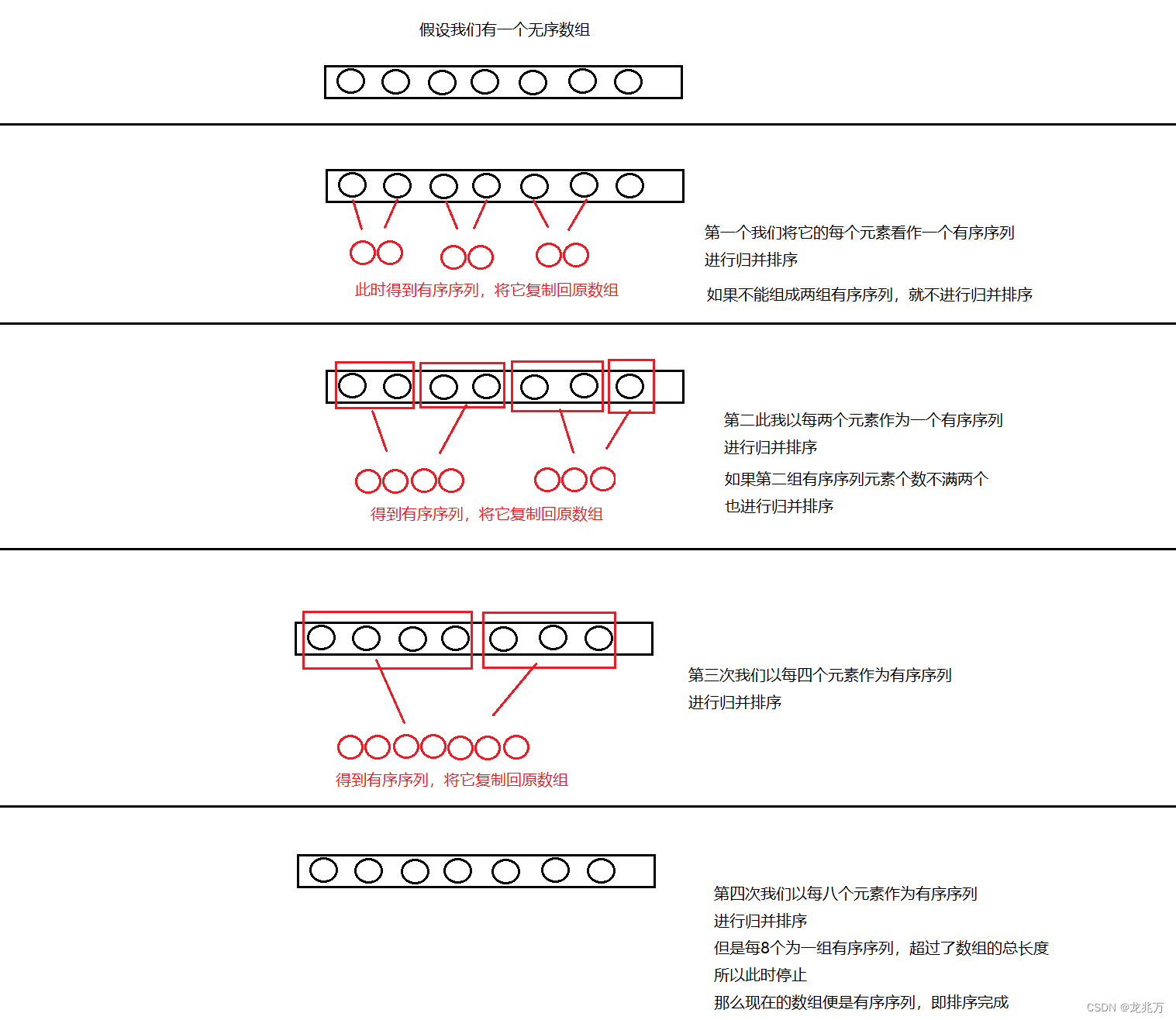
我们用代码描述也非常简单:
void MergeSortNonR(int* a, int n)
{
assert(a);
int* tmp = (int*)calloc(1,sizeof(int) * n);
assert(tmp);
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = begin1;
//如果第一组有序序列没有元素,不排序
if (begin1 >= n)
{
break;
}
//如果第二组有序序列没有元素,不排序
if (begin2 >= n)
{
break;
}
//如果第二组有序序列元素个数不满gap
//就将有效元素组成有序序列排序
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
//每成功归并排序一组,就复制一组
//注意:并不是每一次排序完成再复制回原数组
memcpy(a + i, tmp + i, sizeof(int) * (end2-i + 1));
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
int main()
{
int size = 1000000;
int* arr = (int*)malloc(sizeof(int) * size);
assert(arr);
srand((unsigned int)time(NULL));
for (int i = 0; i < size; i++)
{
arr[i] = rand();
}
//CountSort(arr, size);
//MergeSort(arr, size);
MergeSortNonR(arr, size);
Print(arr, size);
free(arr);
arr = NULL;
return 0;
}