一、介绍
顺序表作为一种基于连续存储空间的数据结构可以有多种应用,本文就以将非纯表转纯表以及求最大子段和的两种方法(递归和动态规划)进行介绍和讲解。
在阅读本文之前建议先了解顺序表的实现,因为顺序表的应用基本是依托顺序表已经实现的部分功能才能实现的,具体可看我的另一篇文章:C++数据结构之线性表——顺序表![]() https://blog.csdn.net/m0_56398315/article/details/126748495?spm=1001.2014.3001.5501
https://blog.csdn.net/m0_56398315/article/details/126748495?spm=1001.2014.3001.5501
为了方便后续的代码读的明白,下图是顺序表中已经实现的函数:
void init();//创建顺序表
void destroy();//销毁顺序表
void clear();//清空顺序表
bool empty();//检测是否为空
int getlength();//获取顺序表的长度
int get(int index);//获取下标为index的元素
int locate(int ele);//查找元素ele所在位置的下标
int prior(int index);//取下标为index的元素的前驱元素
int next(int index);//取下标为index的元素的后继元素
void insert(int ele,int index);//在下标为index的元素位置插入元素ele,原位置的元素依次后移一位
void remove(int index);//删除下标为index的元素,下标index后的元素依次向前移动一位
void traverse();//遍历表
void print();//打印表
void push(int ele);//从表尾插入元素
void batchpush();//批量压入数据二、多余元素删除
概念
1.非纯表
非纯表指的是存在多个相同元素的表,如下图所示就是一个非纯表,其中存在两个相同的元素57

?2.纯表
纯表指的是不存在多个相同元素的表,如下图所示就是一个纯表,其中无法找到两个相同的元素

?实现
要想实现多余元素的删除我们有多种实现方法,有移位删除法和建新表删除法,下面对这两种方法进行一一介绍。
1.移位删除法
算法思想
1.我们以第1个元素为标准,依次对其后面n-1个元素进行比较
2.若发现有和第一个元素相同的元素,那么我们就删除他
3.直到后面n-1个元素检查完毕
4.我们以第2个元素为标准,依次对其后面n-2个元素进行比较
5.若发现有和第二个元素相同的元素,那么我们就删除他
6.直到后面n-2个元素检查完毕
7.以此类推,直到算法执行完毕
算法实现
void sqlist::shiftremove()
{
for (int i = 0; i < length; i++)
{
for (int j = i+1; j < length; j++)
{
if (element[i]==element[j])
{
remove(j);
j--;
}
}
}
}2.建新表删除法
算法思想
首先需要进行说明的是,这个算法的实现基础是表还未建的情况下,因此对于表已经建好了的情况是不适用的
1. 用户输入表的元素个数n
2. 用户输入元素
3. 判断当前表的长度,如果为0说明为空表,直接将该元素作为表的第一个元素
4. 如果不为0说明表不为空表,此时需要对整个表进行遍历检查
5. 如果发现有相同的元素,那么用户输入的该元素就无法插入表中,若没有发现相同的元素就将该元素插入表中
6. 以此类推循环n次,就可以得到一个不含多余元素的表
算法实现
void sqlist::createremove()
{
cout<<"请输入要输入的元素个数:"<<endl;
int elenum;
cin>>elenum;
element=(int*)malloc(elenum*sizeof(int));//分配内存大小为elenum*sizeof(int)的空间
while (elenum--)
{
cout<<"请输入元素element["<<length<<"]:";
int tempele;
cin>>tempele;
if (length==0)
{
element[0]=tempele;
length++;
}
else
{
int i;
for (i = 0; i < length; i++)
{
if (element[i]==tempele)
{
break;
}
}
if (i==length)
{
push(tempele);
}
}
}
}三、求最大子段和
概念
1.子段和
子段和指的是一个表中,连续的一个或多个元素的和,如下图的一个顺序表element[]所示:

?在这个表中我们可以得到多个子段,如element[0]和element[1]可以构成一个子段,因此其子段和为element[0]+element[1]=25+34=59,element[2]和element[3]和element[4]也可以构成一个子段,其子段和为element[2]+element[3]+element[4]=137,当然了,单个元素自身的值也可以是一个子段,其子段和就是其自身的数值
2.最大子段和
最大子段和指的是在表中的一个子段,其子段和大于这个表中其他所有的子段,如下图所示:
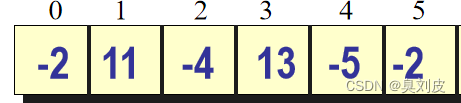
?这个表的一个子段由element[1]、element[2]、element[3]构成,其子段和为20,大于这个表中其他的子段和,因此这个表的最大子段和就是20
实现
1.递归
算法思想
i.最大子段的位置
?设有一个顺序表,我们要求得其最大子段和,那么我们就需要求得他的这个最大子段,而一个表的最大子段只有三种情况:
把一个顺序表分成两半,分别为左半部分:element[0]~element[(length-1)/2] 和右半部分:element[(length-1)/2+1]~element[length-1] ,那么最大子段只能要么全部存在于左半部分,要么全部存在于右半部分,要么处于中间位置(即一部分位于左半部分的尾部一部分位于右半部分的头部)。
了解上面最大子段的位置之后,我们就可以得到:
表的最大子项和=max(左半部分的最大子项和,右半部分的最大子段和,中间部分的最大子段和)
ii.确定递归基
?一个问题要想用递归的思想来做,就必须存在递归基(对递归的基本知识还不清楚的可以看下面的一篇文章:递归(Recursion)_bfhonor的博客-CSDN博客_递归基),那么什么时候会达到递归基呢?我们可以知道,将一个表不断从中“”斩断“再“斩断”,最后会产生单个元素,我们可以知道,单个元素的最大子段和是其本身的值,因此,当不断递归分解直到只剩一个元素的时候我们就达到了递归基,在明确递归基之后我们就可以开始设计递归算法。
iii.设计算法
为了不局限于只能求一整个表的最大子段和,我们设计算法的时候引入了两个参数分别是left和right用来表示表的一个区间,我们在这个区间内来求最大子项和。根据:
表的最大子项和=max(左半部分的最大子项和,右半部分的最大子段和,中间部分的最大子段和)
我们可以知道,要求一个区间内的最大子段和我们需要得到三个最大子段和,分别是左半部分的最大子项和,右半部分的最大子段和,中间部分的最大子段和
左半部分和右半部分的子段和我们可以用递归来求取,但是中间的就不可以了,因此我们需要另外对中间的最大子段和求取进行设计:
求解中间部分最大子项和:
我们可以以中间为起始点,向左添加元素直到将左半部分全部元素添加完,求取左半部分的最大子段和leftmaxsum,同样以中间为起始点,向右添加元素直到将右半部分全部元素添加完,求取右半部分的最大子段和rightmaxsum,两者相加我们就得到了中间部分的最大子段和
最后再把三个部分进行比较就得到了整个区间的最大子段和。
算法实现
int sqlist::r_maxsum(int left,int right)
{
k++;//用来记录递归次数的,可以不用管
int maxsum=0;
if (left==right)//当边界相等的时候说明只有一个元素,达到递归基并将对应值返回
{
if (element[left]>0)//如果该元素大于0
{
maxsum=element[left];//那么其就是最大子段和,
}
else
{
maxsum=0;
}
}
else//当边界不相等时为一般情况
{
int mid=(left+right)/2;//求取中间分界点
//以中间为边界进行递归
int leftsum=r_maxsum(left,mid);//左半部分的递归
int rightsum=r_maxsum(mid+1,right);//右半部分的递归
//求左半部分的最大子段和
int leftmaxsum=0;//用来存储左半部分的最大字段和
int templeftmaxsum=0;//用来存储左半部分当前的子段和
for (int i = mid; i >=left; i--)//由中间向左边扩散
{
templeftmaxsum=templeftmaxsum+element[i];//每次向左加一个数
if (templeftmaxsum>leftmaxsum)//如果发现加完后子段和变大了
{
leftmaxsum=templeftmaxsum;//那么更新最大子段和
}
}
//求右半部分的最大子段和
int rightmaxsum=0;//用来存储右半部分的最大字段和
int temprightmaxsum=0;//用来存储右半部分当前的字段和
for (int j = mid+1; j <=right; j++)//由中间向右边扩散
{
temprightmaxsum=temprightmaxsum+element[j];//每次向左加一个数
if (temprightmaxsum>rightmaxsum)//如果发现加完后子段和变大了
{
rightmaxsum=temprightmaxsum;//那么更新最大子段和
}
}
maxsum=leftmaxsum+rightmaxsum;//子段和合并得到中间部分的最大子段和
if (maxsum<leftsum)//比较三者的大小并返回最大的子段和
{
maxsum=leftsum;
}
else if (maxsum<rightsum)
{
maxsum=rightsum;
}
}
//返回最大子项和
return maxsum;
}2.动态规划
算法思想
引用动态规划前的思考
我们可以知道,一个表一般来说由多个数据组成,有正数也有负数,那么我们可以思考一个问题:
当 当前的子段和为负数的时候,我们是否应该继续往下添加元素将该元素与该子段和相加?为了让读者更加容易读懂,我接下来进行一个举例:

?如上图是一个长度为7的顺序表,我们为了求得最大子段和,我们先从左边的元素开始加起,我们设子段和为max, max=element[0]=2 我们继续相加, max=element[0]+element[1]=-2 ,此时我们是否应该继续往下加入元素element[2],答案是否 ,为什么呢?我们可以这样想,既然当前的子段和已经小于0了,那么我为什么不舍弃掉前面的子段和,直接找到后面的第一个正数作为我们的子段和的第一个元素呢,即:
max=element[0]+element[1]+element[2]=1?? <??? max1=element[2]
当掌握了这个思想之后我们就可以引入动态规划的思想了
动态规划
本问题中动态规划的核心就是创建一个变量maxsum表示当前的最大子段和以及一个变量sum用来表示当前操作的子段和,每次我们添加元素之后sum的值就会发生变动,如果我们发现sum比maxsum小的话说明当前添加的元素为负数因此并没有使得子段和变大,此时我们并不停下“前进的脚步“”,继续添加下一个元素,添加完下一个元素之后继续比较maxsum和sum的值,如果此时发现sum>maxsum说明当前添加的元素能使得子段和变大,此时我们就将sum的值赋给maxsum,然后继续向前添加元素,以此类推。
算法实现
int sqlist::d_maxsum()
{
int sum=0,maxsum=0;//初始化最大子段和当前子段和为0
for (int i = 0; i < length; i++)
{
sum+=element[i];//当前子段和更新
if (sum<0)//判断所加的第一个元素是否为正数且判断当前子段和是否小于0
{
sum=0;//如果所加的第一个数不是正数或当前子段和小于0的话说明前面的子段全部作废,直接查找下一个正数
}
if (sum>maxsum)//如果当前子段和大于最大子段和的话
{
maxsum=sum;//更新最大子段和
}
}
return maxsum;//返回最大子段和
}代码执行结果
我们对下图这么一个表进行求最大子段和的操作:
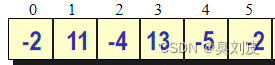
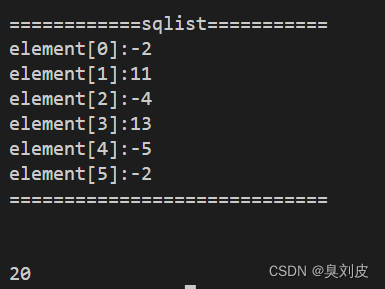
?我们可以求得最大子段和为20,验证了算法的正确性。
三、总结
本文对顺序表的多余元素的删除以及求最大子段和进行了不同方法的实现,多余元素的删除相对而言比较简单,求最大子段和的动态规划方法也比较简单,但是递归方法比较复杂,需要多看代码进行分析,如果喜欢本文的话麻烦动动你的小手点点赞哦!???