目录
冒泡排序
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
动图演示
????????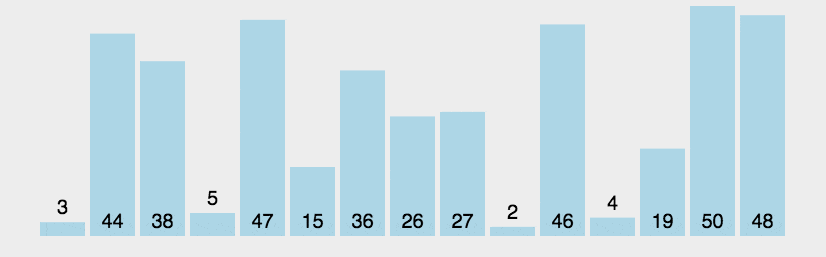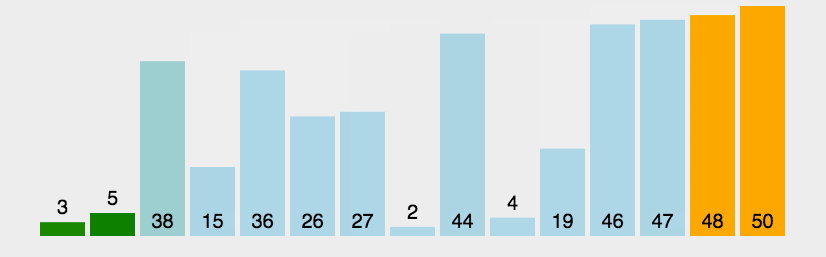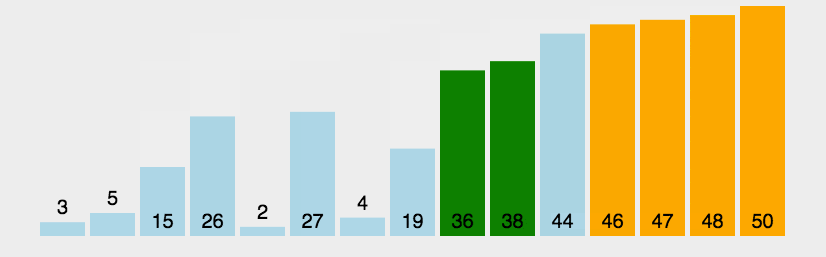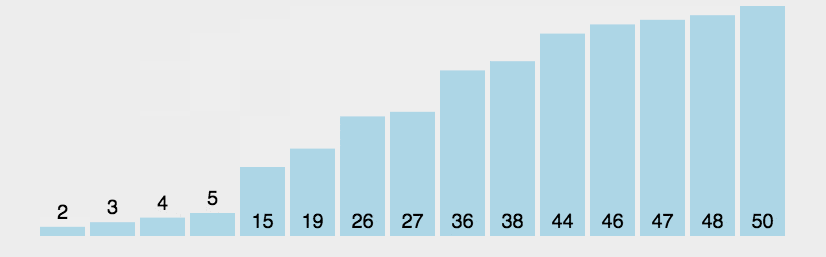
?
?代码实现
#include <stdio.h>
#include <stdbool.h>
void BubbleSort(int* arr, int n)
{
//如果传入数组为空,或数组内元素数目小于等于1,则无需排序
if(arr == NULL || n <= 1)
{
retrun;
}
//如果有n个元素,那么最多只需要排n-1趟即可
for(int i = 0; i < n - 1; i++)
{
bool flag = true;
for(int j = 0; j < n - 1; j++)
{
if(arr[j] > arr[j + 1])
{
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = false;
}
}
if(flag)
{
break;
}
}
}?
选择排序
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
动图演示
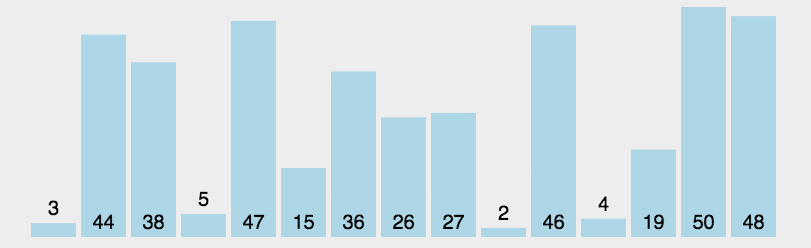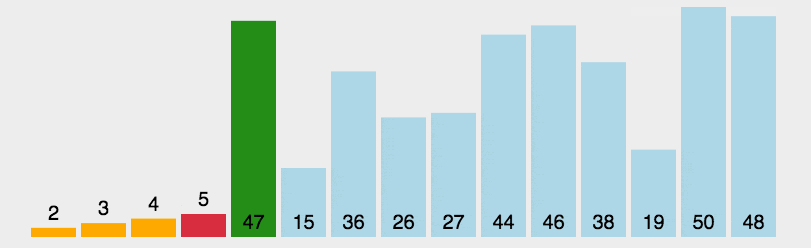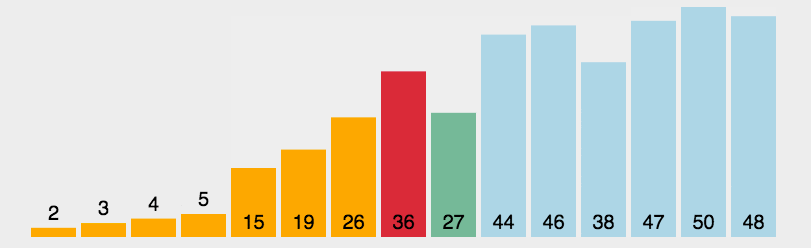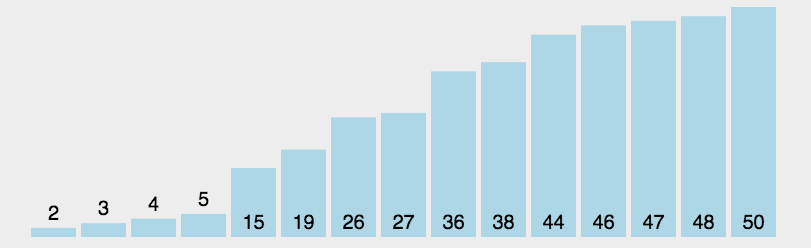
?代码实现
#include <stdio.h>
void SelectSort(int* arr, int n)
{
//如果传入数组为空,或数组内元素数目小于等于1,则无需排序
if (arr == NULL || n <= 1)
{
return;
}
//如果有n个元素,那么最多只需要排n-1趟即可
for (int i = 0; i < n - 1; i++)
{
int index = i;
for (int j = i; j < n; j++)
{
if (arr[index] > arr[j])
{
index = j;
}
}
if (index != i)
{
int tmp = arr[i];
arr[i] = arr[index];
arr[index] = tmp;
}
}
}插入排序
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
动图演示
 ?
?
代码实现
#include <stdio.h>
void InsertSort(int* arr, int n)
{
//如果传入数组为空,或数组内元素数目小于等于1,则无需排序
if (arr == NULL || n <= 1)
{
return;
}
//由于要与前一个元素作比较,所以i=0无意义,直接从第2个元素也就是下标为1的元素开始
for (int i = 1; i < n; i++)
{
int tmp = arr[i];
int j = i - 1;
//当前待比较元素下标有效并且此元素大于tmp,进入循环
while (j >= 0 && arr[j] > tmp)
{
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = tmp;
}
}?
希尔排序
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
?动图演示
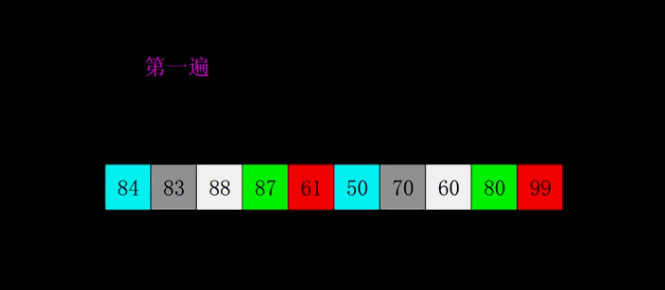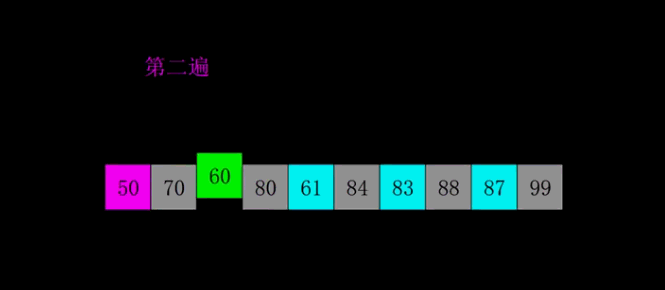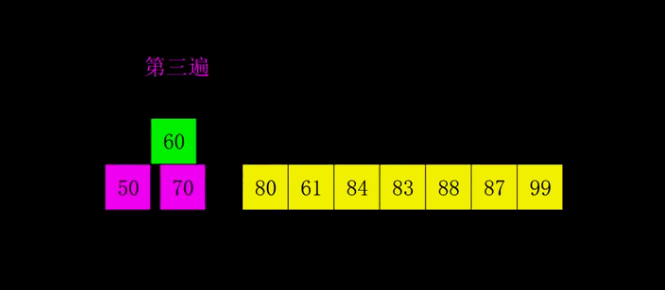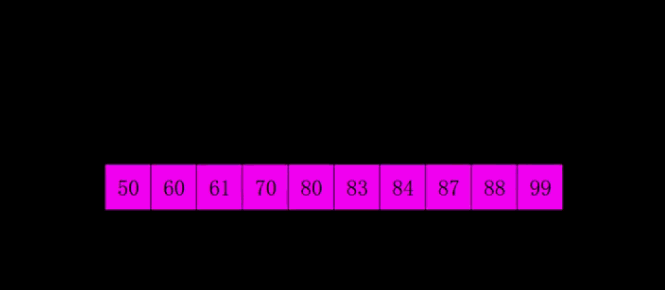
?
代码实现
#include <stdio.h>
void ShellSort(int* arr, int n)
{
//如果传入数组为空,或数组内元素数目小于等于1,则无需排序
if (arr == NULL || n <= 1)
{
return;
}
//分组获取步长
int step = n / 2;
int i, j, tmp;
while (step)
{
for (i = step; i < n; i++) {
tmp = arr[i];
j = i - step;
//保证组内有序
while (j >= 0 && arr[j] > tmp)
{
arr[j + step] = arr[j];
j -= step;
}
arr[j + step] = tmp;
}
step /= 2;
}
}
快速排序 hoare
动图演示
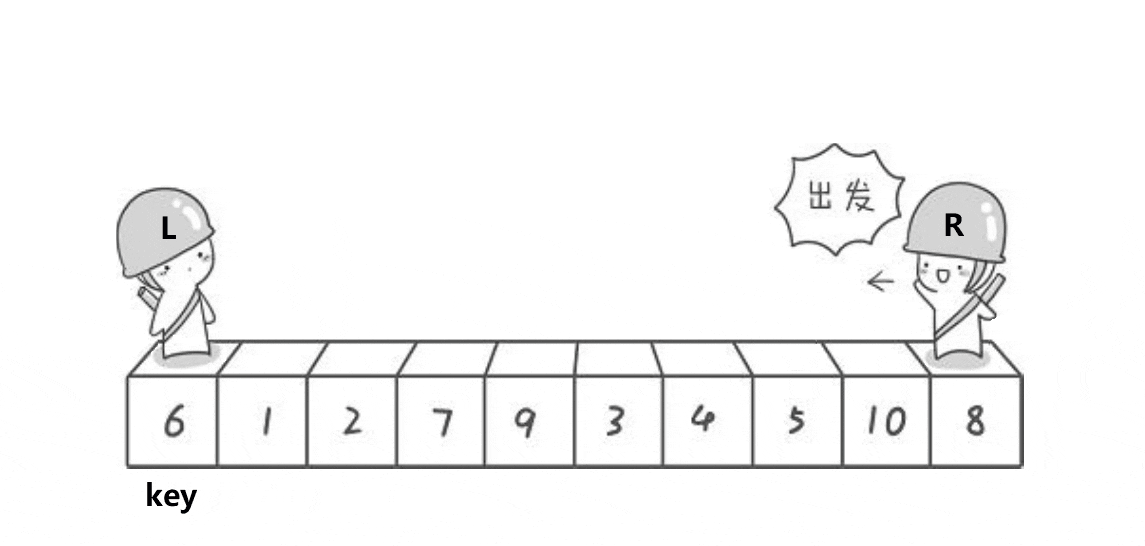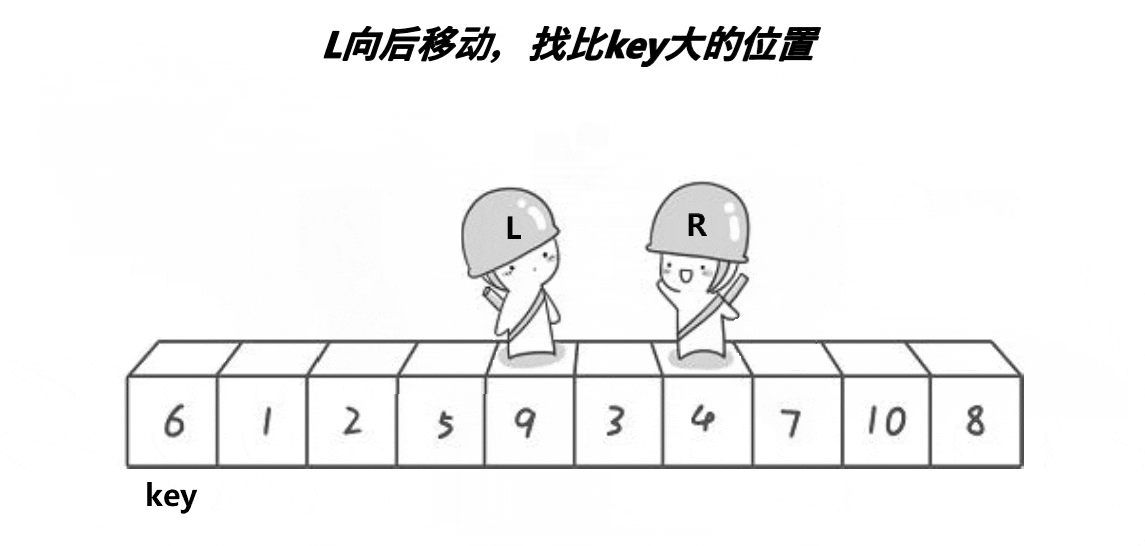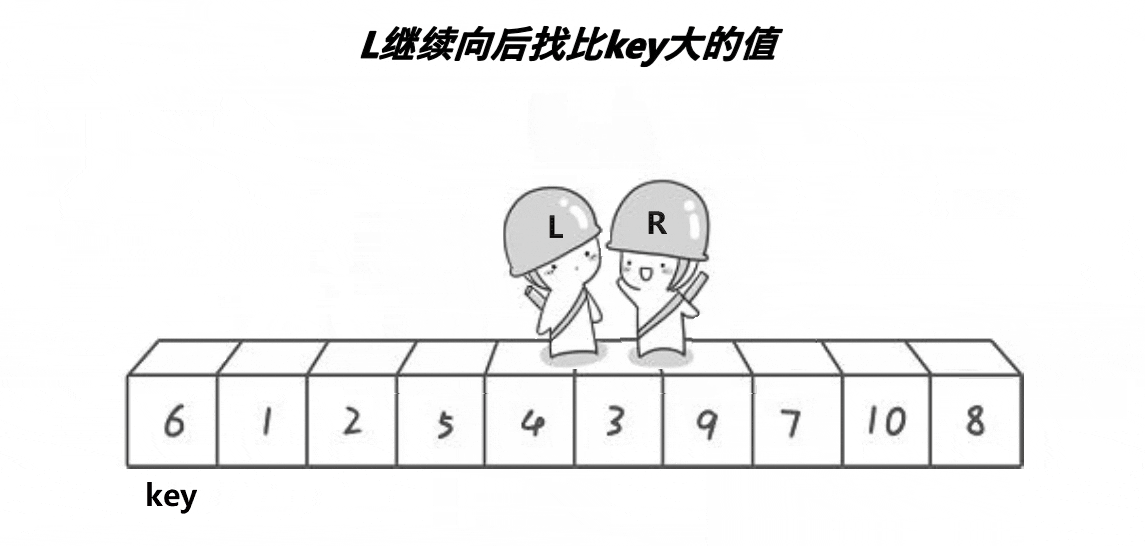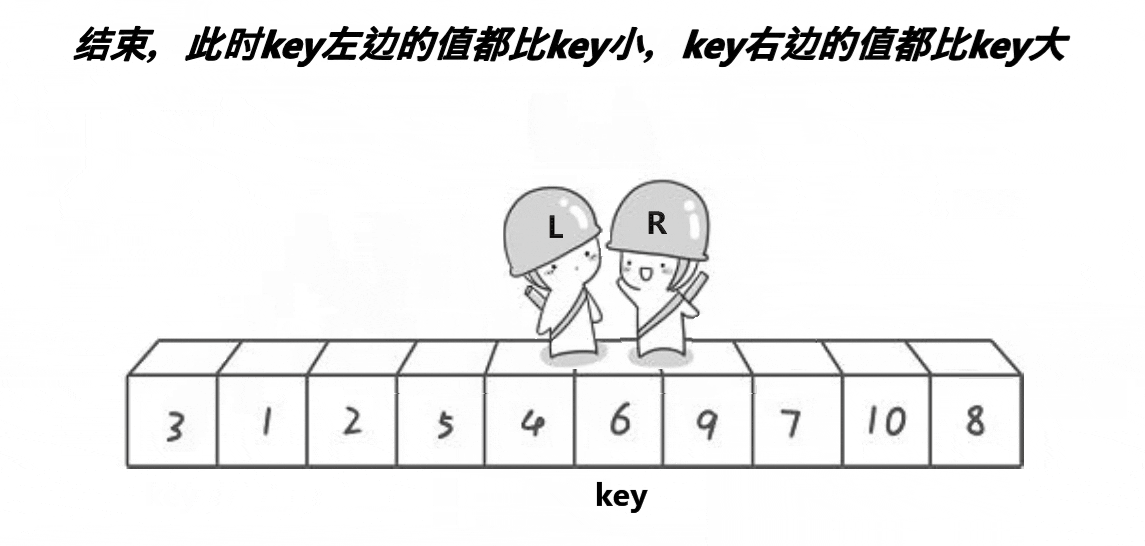
?
代码实现
#include<iostream>
using namespace std; //为了使用系统中的swap函数,可以自己实现
//三数取中 --- 获取中间值,尽量使每次递归式左右数据量相等
void helper(int* arr, int left, int right);
int getMidPos(int* arr, int left, int right)
{
int mid = left + ((right - left) >> 1);
int max = arr[left] > arr[right] ? left : right;
int min = left - max + right;
if (arr[mid] > arr[max])
{
return max;
}
return arr[mid] > arr[min] ? mid : min;
}
void QuickSort(int* arr, int n)
{
//如果传入数组为空或只有一个数据或没有数据直接返回
if (arr == NULL || n <= 1)
{
return;
}
helper(arr, 0, n - 1);
}
void helper(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int index = getMidPos(arr, left, right);
swap(arr[index], arr[left]);
int key = arr[left];
int L = left;
int R = right;
while (left < right)
{
while (left < right && arr[right] > key)
{
right--;
}
while (left < right && arr[left] <= key)
{
left++;
}
swap(arr[left], arr[right]);
}
swap(arr[L], arr[left]);
helper(arr, L, left - 1);
helper(arr, left + 1, R);
}
快速排序 挖坑法
动图演示
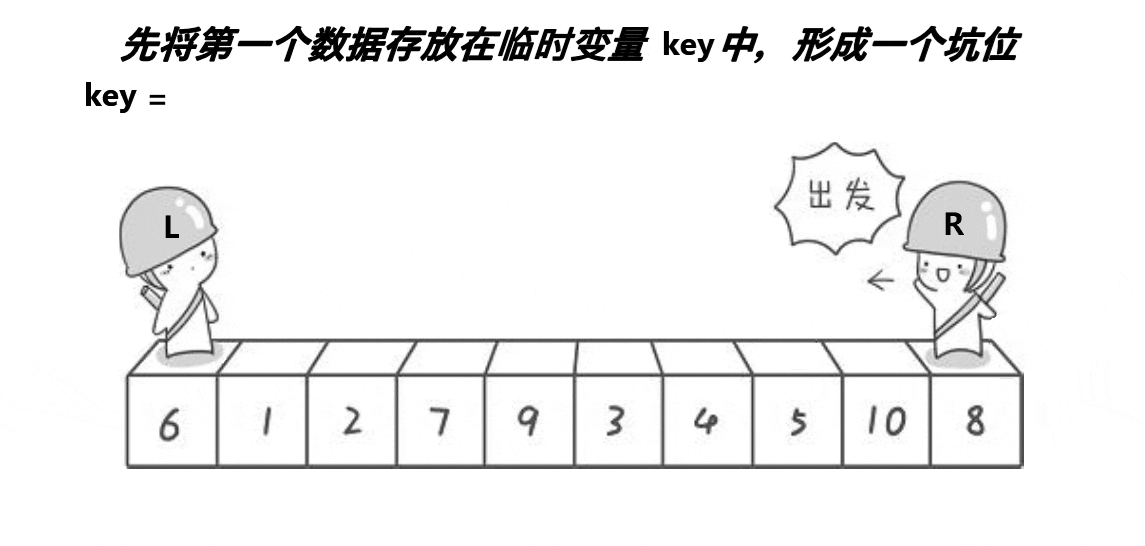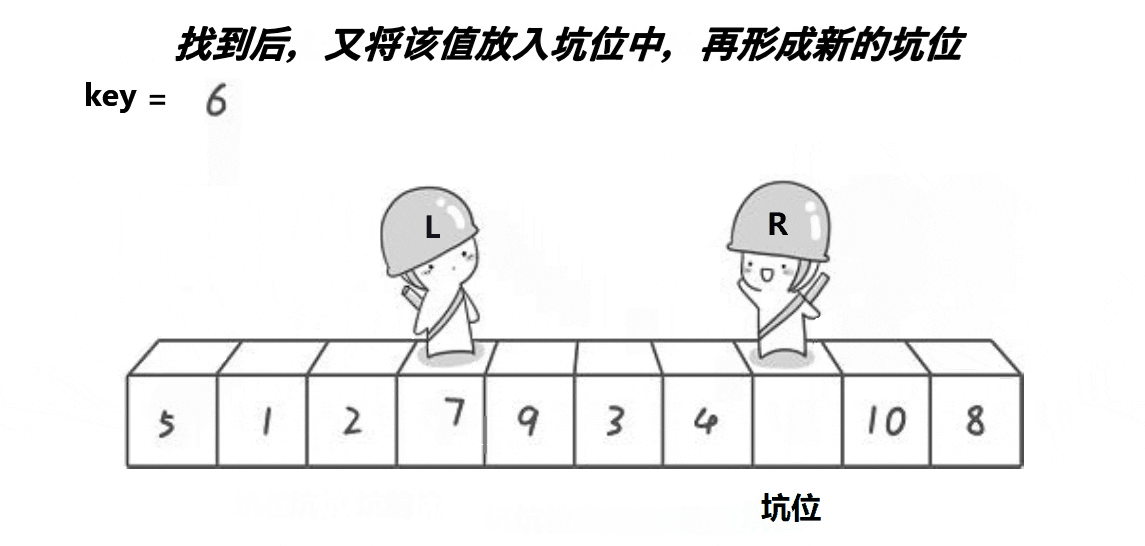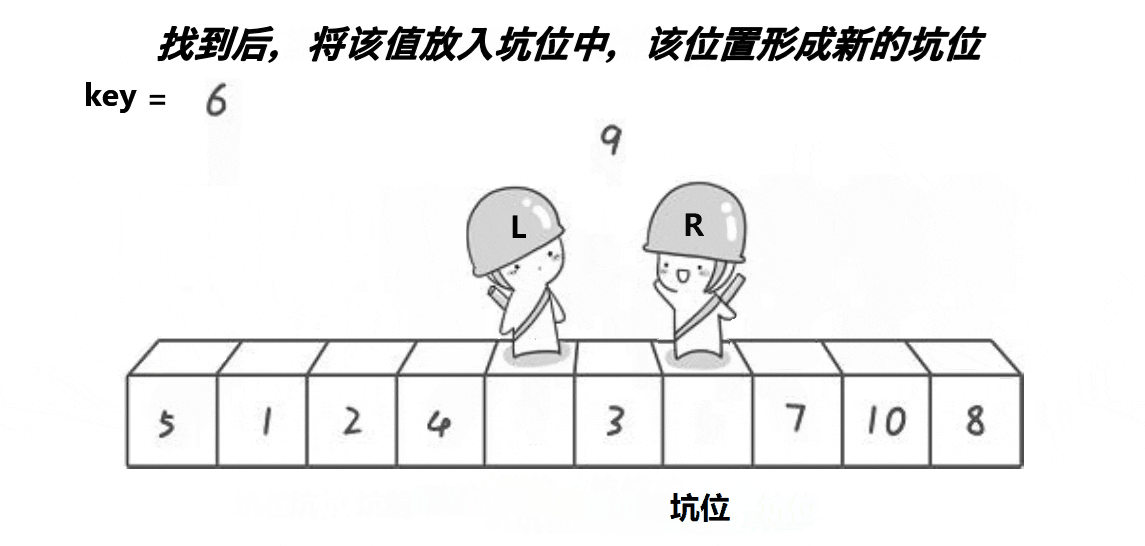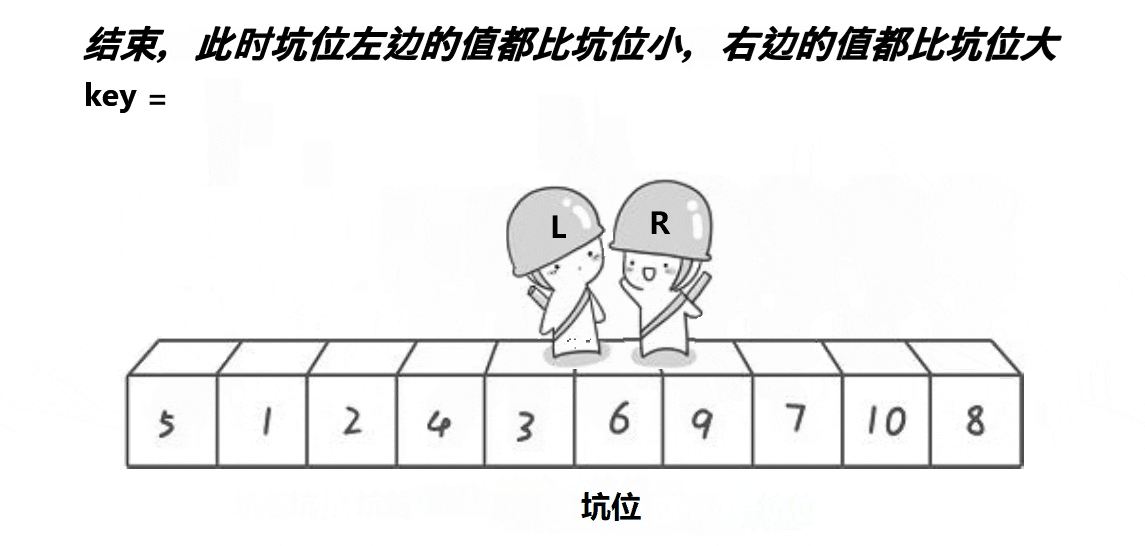
?
代码实现
?
#include<iostream>
using namespace std; //为了使用系统中的swap函数,可以自己实现
//三数取中 --- 获取中间值,尽量使每次递归式左右数据量相等
void helper(int* arr, int left, int right);
int getMidPos(int* arr, int left, int right)
{
int mid = left + ((right - left) >> 1);
int max = arr[left] > arr[right] ? left : right;
int min = left - max + right;
if (arr[mid] > arr[max])
{
return max;
}
return arr[mid] > arr[min] ? mid : min;
}
void QuickSort(int* arr, int n)
{
//如果传入数组为空或只有一个数据或没有数据直接返回
if (arr == NULL || n <= 1)
{
return;
}
helper(arr, 0, n - 1);
}
void helper(int* arr, int left, int right)
{
if (right <= left)
{
return;
}
int index = getMidPos(arr, left, right);
swap(arr[index], arr[left]);
int L = left;
int R = right;
int hole = left;
int key = arr[left];
while (L < R)
{
while (L < R && arr[R] > key)
{
R--;
}
arr[hole] = arr[R];
hole = R;
while (L < R && arr[L] <= key)
{
L++;
}
arr[hole] = arr[L];
hole = L;
}
arr[hole] = key;
helper(arr, left, hole - 1);
helper(arr, hole + 1, right);
}
快速排序 前后指针法
动图演示
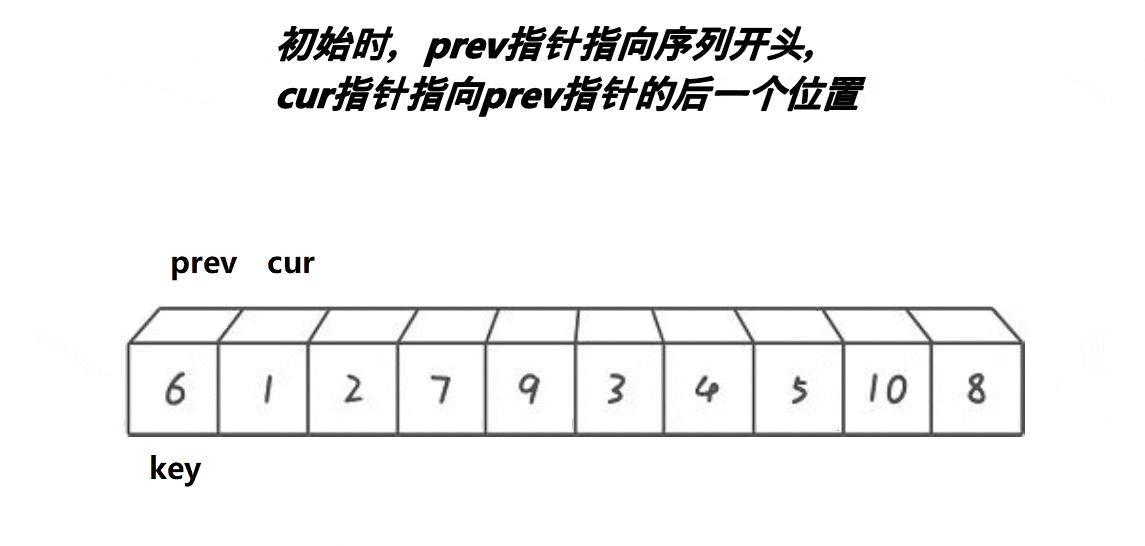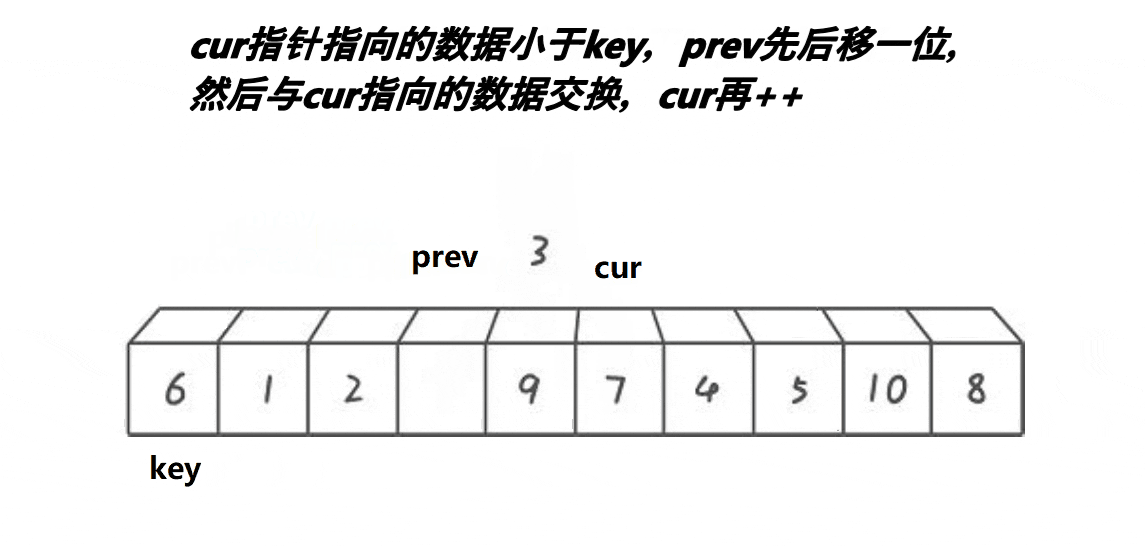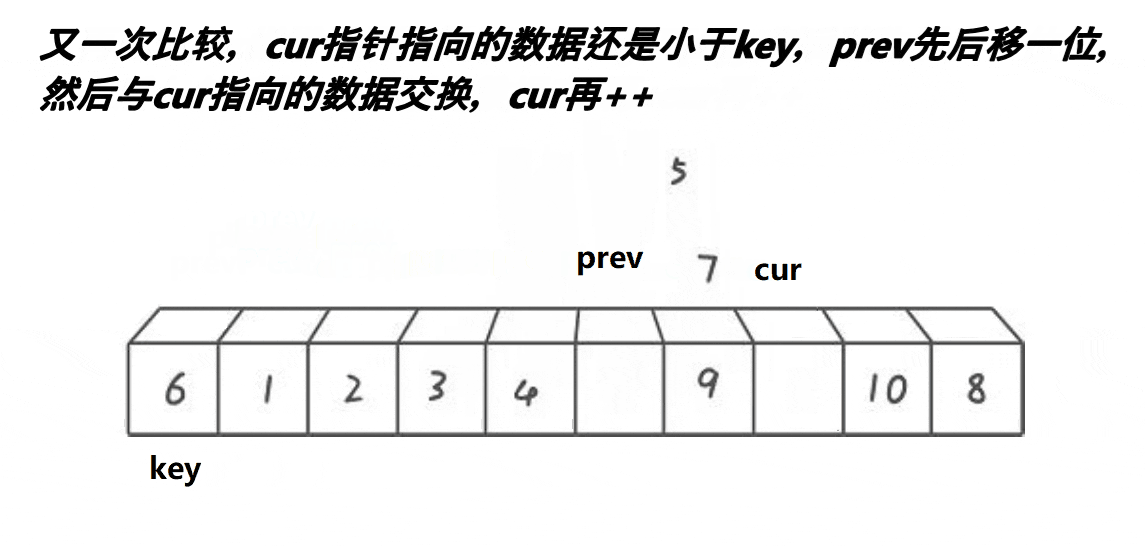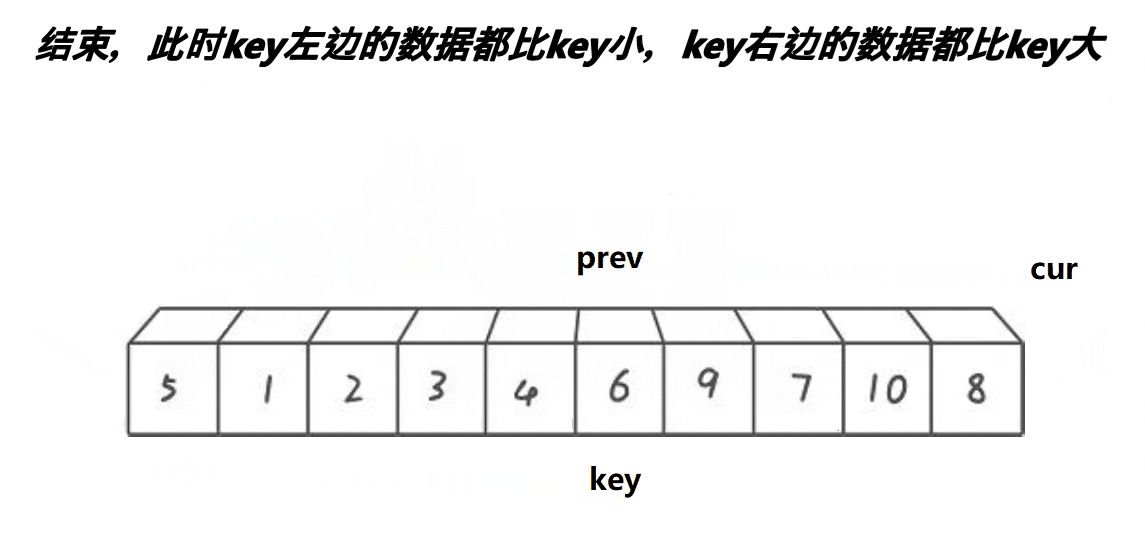
?
代码实现
#include<iostream>
using namespace std; //为了使用系统中的swap函数,可以自己实现
//三数取中 --- 获取中间值,尽量使每次递归式左右数据量相等
void helper(int* arr, int left, int right);
int getMidPos(int* arr, int left, int right)
{
int mid = left + ((right - left) >> 1);
int max = arr[left] > arr[right] ? left : right;
int min = left - max + right;
if (arr[mid] > arr[max])
{
return max;
}
return arr[mid] > arr[min] ? mid : min;
}
void QuickSort(int* arr, int n)
{
//如果传入数组为空或只有一个数据或没有数据直接返回
if (arr == NULL || n <= 1)
{
return;
}
helper(arr, 0, n - 1);
}
void helper(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int index = getMidPos(arr, left, right);
swap(arr[index], arr[left]);
int prev = left;
int cur = left + 1;
int key = arr[left];
while (cur <= right)
{
while (cur <= right && arr[cur] > key)
{
cur++;
}
if (cur > right)
{
break;
}
prev++;
if (prev != cur)
{
swap(arr[prev], arr[cur]);
}
else
{
cur++;
}
}
swap(arr[prev], arr[left]);
helper(arr, left, prev - 1);
helper(arr, prev + 1, right);
}
快速排序? 一次拍一组
-
从数列中挑出一个元素,称为 "基准"(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序
动图演示
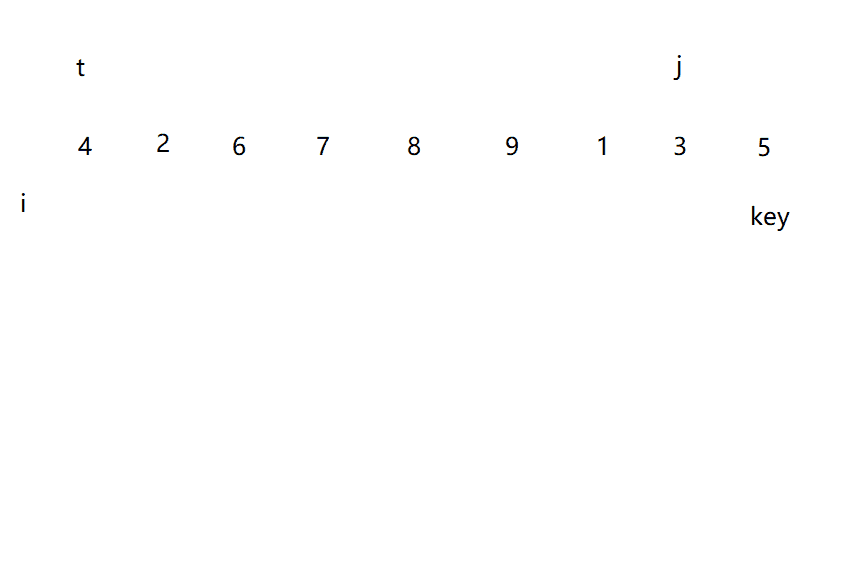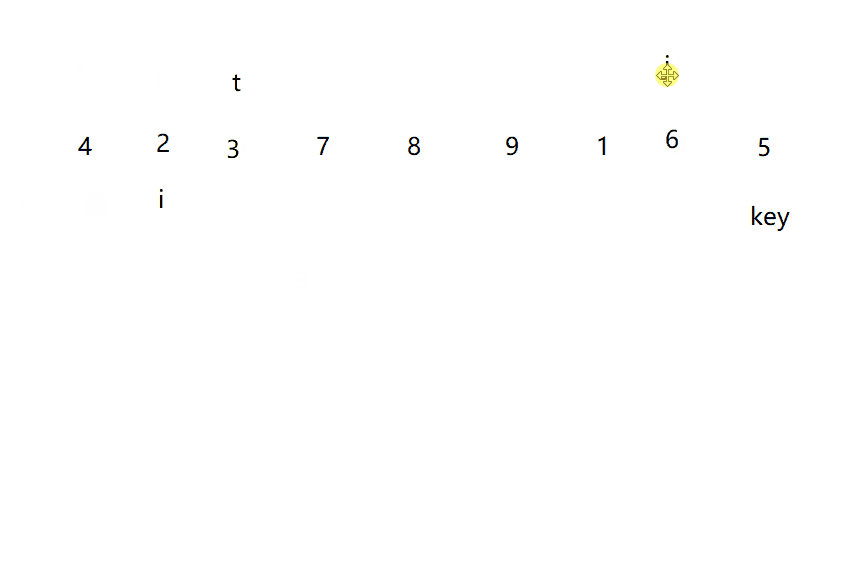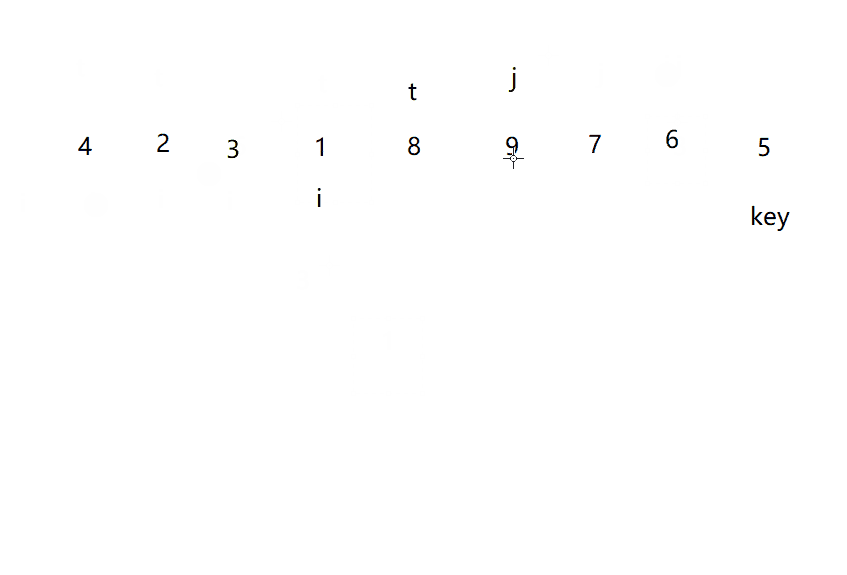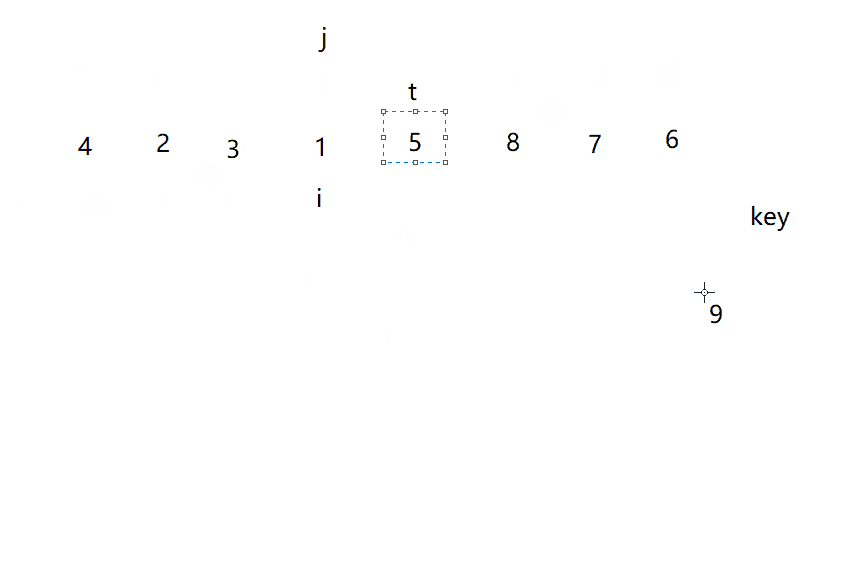
?
代码实现
void helper(int* arr, int left, int right);
int getMidPos(int* arr, int left, int right)
{
int mid = left + ((right - left) >> 1);
int max = arr[left] > arr[right] ? left : right;
int min = left - max + right;
if (arr[mid] > arr[max])
{
return max;
}
return arr[mid] > arr[min] ? mid : min;
}
void QuickSort(int* arr, int left, int right)
{
//如果传入数组为空或只有一个数据或没有数据直接返回
if (arr == NULL || right <= left)
{
return;
}
helper(arr, left, right);
}
void helper(int* arr, int left, int right)
{
if (right <= left)
{
return;
}
int index = getMidPos(arr, left, right);
swap(arr[index], arr[right]);
int i = left - 1;
int t = left;
int j = right;
while (t < j)
{
if (arr[t] > arr[right])
{
j--;
swap(arr[t], arr[j]);
t--;
}
else if (arr[t] < arr[right])
{
i++;
swap(arr[t], arr[i]);
}
t++;
}
swap(arr[j], arr[right]);
helper(arr, left, i);
helper(arr, j + 1, right);
}
归并排序
动图演示
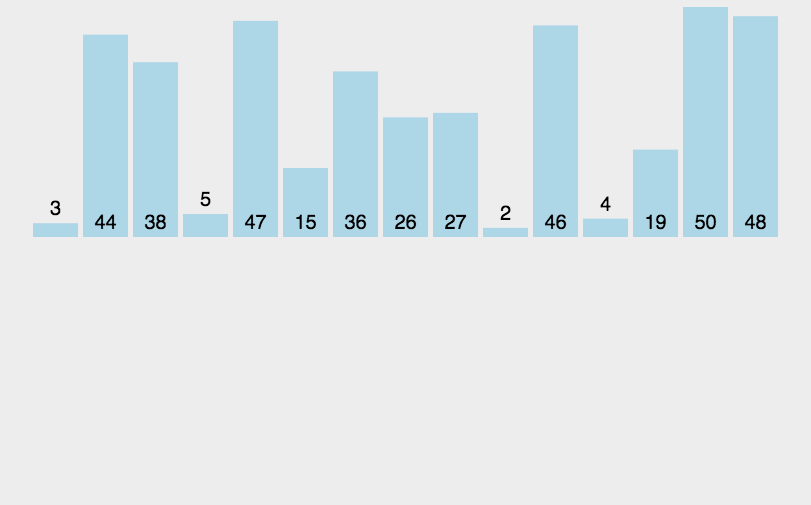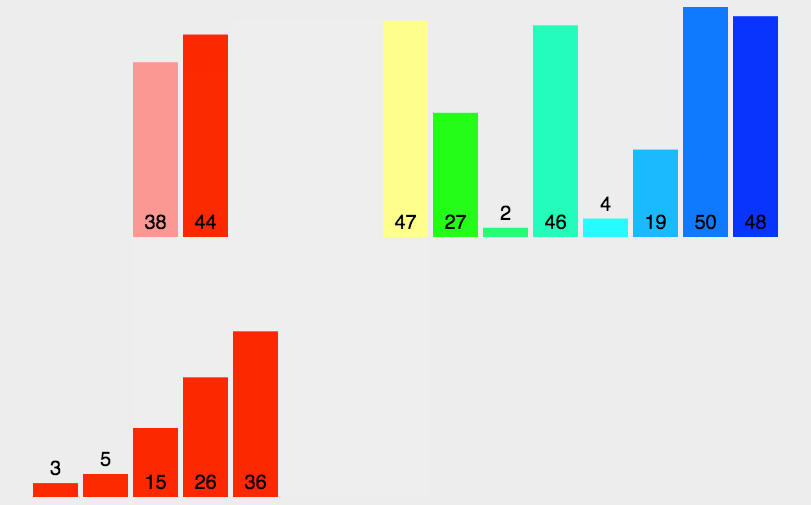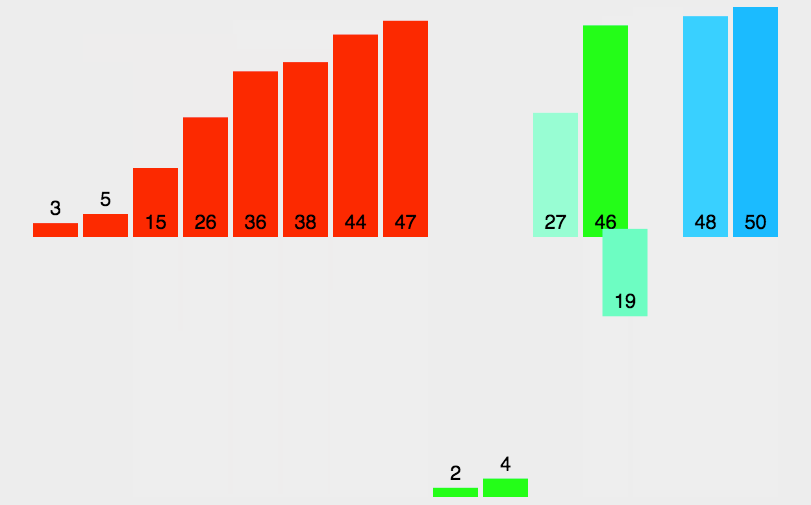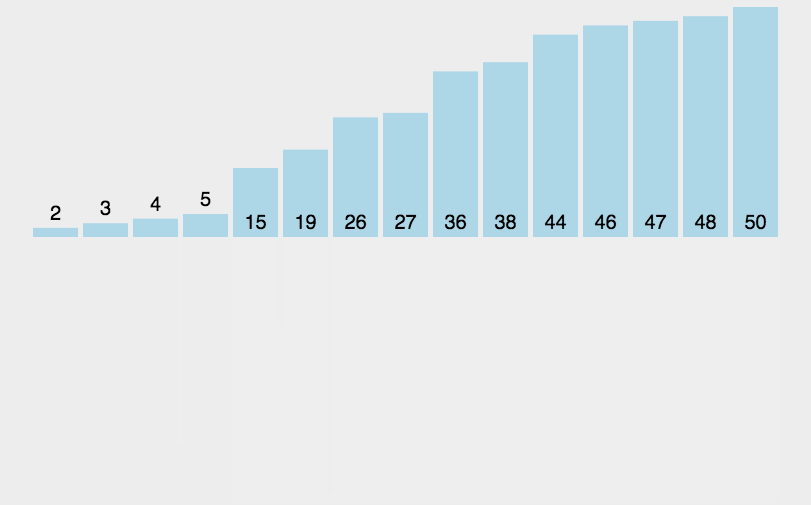
?
代码实现
#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
void Merge(int* arr, int left, int mid, int right, int* tmp);
void Partion(int* arr, int left, int right, int* tmp);
void MergeSort(int* arr, int n)
{
if (left >= right || NULL == arr)
{
return;
}
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
Partion(arr, 0, n - 1, tmp);
free(tmp);
}
void Partion(int* arr, int left, int right, int* tmp)
{
if (left == right)
{
return;
}
int mid = left + (right - left) / 2;
Partion(arr, left, mid, tmp);
Partion(arr, mid + 1, right, tmp);
Merge(arr, left, mid, right, tmp);
}
void Merge(int* arr, int left, int mid, int right, int* tmp)
{
int i = left;
int j = mid + 1;
int t = 0;
while (i <= mid && j <= right)
{
if (arr[i] > arr[j])
{
tmp[t++] = arr[j];
}
else
{
tmp[t++] = arr[i];
}
}
while (i <= mid)
{
tmp[t++] = arr[i++];
}
while (j <= right)
{
tmp[t++] = arr[j++];
}
i = 0;
while (i < t)
{
arr[left + i] = tmp[i];
i++;
}
}
归并排序非递归
代码实现
void MergeSortNoR(int* arr, int n)
{
if (NULL == arr || n <= 1)
{
return;
}
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
for (int step = 1; step < n; step *= 2)
{
for (int j = 0; j < n; j += 2 * step)
{
int begin1 = j, end1 = j + step;
int begin2 = j + step, end2 = j + 2 * step;
int t = begin1;
if (begin2 >= n)
{
if(step == 1)
{
tmp[t] = arr[begin1];
}
break;
}
if (end2 > n)
{
end2 = n;
}
while (begin1 < end1 && begin2 < end2)
{
if (arr[begin1] > arr[begin2])
{
tmp[t++ + left] = arr[begin2++];
}
else
{
tmp[t++ + left] = arr[begin1++];
}
}
while (begin1 < end1)
{
tmp[t++ + left] = arr[begin1++];
}
while (begin2 < end2)
{
tmp[t++ + left] = arr[begin2++];
}
}
memcpy(arr, tmp, n * sizeof(ElemType));
}
}堆排序
动图演示

?
代码实现
void AdjustUp(int* arr, int child);
void Heapify(int* arr, int n);
void HeapSort(int* arr, int n)
{
if (arr == NULL || n <= 1)
{
return;
}
int HeapSize = n;
for (int i = 0; i < HeapSize; i++)
{
AdjustUp(arr, i);
}
while (HeapSize > 1)
{
Swap(&arr[HeapSize - 1], &arr[left]);
HeapSize--;
Heapify(arr, HeapSize);
}
}
void AdjustUp(ElemType* arr, int child)
{
int parent = (child - 1) / 2;
while (arr[parent] < arr[child])
{
Swap(&arr[parent], &arr[child]);
child = parent;
parent = (child - 1) / 2;
}
}
void Heapify(ElemType* arr, int n)
{
int parent = 0;
int leftChild = parent * 2 + 1;
while (leftChild < n)
{
int largest = leftChild + 1 < n && arr[leftChild + 1] > arr[leftChild] ? leftChild + 1 : leftChild;
largest = arr[largest] > arr[parent] ? largest : parent;
if (parent = largest)
{
break;
}
Swap(&arr[largest], &arr[parent]);
parent = largest;
leftChild = parent * 2 + 1;
}
}