贪心
定义:贪心是求解一类最优化问题的方法,它总是考虑在当前状态下局部最优(或较优) 的策略,来使全局的结果达到最优(或较优)。显然,如果采取较优而非最优的策略(最优策略可能不存在或是不易想到),得到的全局结果也无法使用最优的。而要获得最优结果,则要求中间的每步策略都是最优的,因此严谨使用贪心法来求解最优化问题需要对采取的策略进行证明,证明的一般思路是使用反证法及数学归纳法,即假设策略不能导致最优解,然后通过系列推导来得到矛盾,以此证明策略是最优的,最后用数学归纳法保证是全局最优。不过平常使用无须严格证明。因此,如果在想到某个似乎可行的策略,并且自己无法举出反例,那就勇敢的实现它。
一般贪心
矩阵消除游戏
题目描述
链接:牛妹在玩一个名为矩阵消除的游戏,矩阵的大小是n行m列,第i行第j列的单元格的权值为ai,j,牛妹可以进行k个回合的游戏,在每个回合,牛妹可以选择一行或者选择一列,然后将这一行或者这一列的所有单元格中的权值变为0,同时牛妹的分数会加上这一行或者这一列中的所有单元格的权值的和。
牛妹想最大化她的得分,球球你帮帮她吧!
输入描述
第一行三个整数n,m,k
接下来n行每行m个整数表示矩阵中各个单元格的权值
输出描述
输出一个整数表示牛妹能获得的最大分数。
示例一
输入
3 3 2
101 1 102
1 202 1
100 8 100
输出
414
备注
1≤n,m≤15
1≤ai,j≤1e6
1≤k≤n?m
思路
- 这是一道不算太难的贪心、枚举题(但是自己做了很久,还WA了很多次)
- 我第一次做的时候想的是:如果我每次贪心的选剩下的图中最大的一行或者一列,然后把这一行(列)抹为0 ,但是很明显,这个方法的错误在于你抹了0会对后面的贪心选择造成影响
- 使用01串枚举(二进制枚举)
- 用行开始枚举
题解
#include<bits/stdc++.h>
using namespace std;
int n,m,k,a[20][20];
long long sh[20],sl[20],ans;
bool b[20]; //记录被选中的行的序号
bool cmp(int a,int b) {
return a>b;
}
int deal(int x) {
memset(b,0,sizeof b);
int cnt=0,i=1;
while(x) {
if(x&1) { //检测最后一个数字是否为1,如果为1就++cnt,并记录行序号i
++cnt;
b[i]=1;
}
x>>=1; //右移一位,相当于从右往左依次检测
++i;
}
return cnt;
}
int main() {
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j) {
scanf("%d",&a[i][j]);
sh[i]+=a[i][j];
}
if (k > n) k=n;
if (k > m) k=m;
int tmp=(1<<n)-1; //枚举的总个数为2的n次方个(对于每一行有2个选择,选中或不选中)
for(int x=0;x<=tmp;++x) { //要从0开始,因为一行也不选需要纳入考量范围
int numh=deal(x);
int numl=k-numh;
if(numl<0) continue;
long long sum=0;
for (int i = 1; i <= n; i++)
if(b[i]) sum+=sh[i]; //被选中的行,加起来
memset(sl, 0, sizeof(sl));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(!b[i]) sl[j]+=a[i][j]; //从列开始汇总,在行中被选用的不纳入
sort(sl+1, sl+1+m,cmp); //从大到小排序,贪心选择值最大的列
for(int i=1;i<=numl;++i) sum += sl[i];
ans=max(ans,sum);
}
printf("%lld\n", ans);
return 0;
}
推公式
[USACO 2007 Jan S]Protecting the Flower


思路
- 初看题目,知道minimize意味着要使用贪心算法,每一步都要作出小的选择
- 推公式 —— 任意选出两头牛进行贪心排序,可以看到有2种排法(a,b、b,a)
- (a,b)那么第二头牛的破坏量就是ta*db*2
- (a,b)那么第二头牛的破坏量就是tb*da*2
- 比较两个排法即可
- 用数学归纳法推广到整个数组
题解
#include <bits/stdc++.h>
using namespace std;
pair<int,int> p[100005];
bool cmp(pair<int,int> a,pair<int,int> b){
return a.first*b.second<b.first*a.second;
}
int main(){
int n;
cin >>n;
for(int i=0;i<n;++i){
cin>>p[i].first>>p[i].second;
}
sort(p,p+n,cmp);
long long sum=0, ans=0;
for(int i=0;i<n;++i){
ans+=sum*p[i].second;
sum+=p[i].first;
}
ans*=2;
cout <<ans <<endl;
return 0;
}
注意对pair使用sort排序,默认比较pair.first,也可以自己写bool函数自定义
按位贪心
兔子的区间密码
题目描述
有一只可爱的兔子被困在了密室了,密室里有两个数字,还有一行字:
只有解开密码,才能够出去。
可爱的兔子摸索了好久,发现密室里的两个数字是表示的是一个区间[L,R]
而密码是这个区间中任意选择两个(可以相同的)整数后异或的最大值。
比如给了区间[2,5] 那么就有2 3 4 5这些数,其中 2 xor 5=7最大 所以密码就是7。
兔子立马解开了密室的门,发现门外还是一个门,而且数字越来越大,兔子没有办法了,所以来求助你。
提示:异或指在二进制下一位位比较,相同则 0 不同则 1
例如2=(010)2, 5=(101)2
?所以2 xor 5=(111)2=7
输入描述
第一行一个数 T,表示数据组数。
接下来 T 行,每行两个数 L,R, 表示区间[L,R]
输出描述
输出共T行每行一个整数,表示[L,R]的密码
示例一
输入
5
1 10
2 3
3 4
5 5
2 5
输出
15
1
7
0
7
备注
对于30%的数据
1 ≤ T ≤ 10
0 ≤ L ≤ R ≤ 100
对于另外10%的数据
L=R
对于70%的数据
1 ≤ T ≤ 10
0 ≤ L ≤ R ≤ 50000
对于100%的数据
1 ≤ T ≤ 10000
0 ≤ L ≤ R ≤ 1018
(对于100%的数据) 输入数据较大,请使用快速读入。
思路
- 这道题没有好的方法就不简单,但是找到好的切入点就比较清晰了
- L<=R,那么换成二进制就会有2种结果:
- L的位数=R的位数(L=(1000)2,R=(1011)2)
- L的位数比R的小(L=(100)2,R=(1000)2)
- 可以看出,在这个区间上要找到异或值最大的数就是要找不同的位数最大的数。如果我们比较L和R的每一位,当发现第一个不同的数字时,就可以确定结果了
- 假设确定的位置数为i,那么,2i+1-1——就能造出一个含1最多的数(0111……),而这个区间内肯定存在相应的含0最多的数(0000……),此时,这两个数异或就得到区间最大值
- 题目中提到了快速读入,但是这道题就算没用快速读入也可以AC。
不代表不需要知道快速读入😪
要使用 inline,因为一般要使用到 快速读入 的时候都会频繁调用,这段代码考虑到了负数
inline int read(){
int x=0,y=1;char c=getchar();
while (c<'0'||c>'9') {if (c=='-') y=-1;c=getchar();}
while (c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
题解
#include<bits/stdc++.h>
using namespace std;
int t,i;
typedef long long ll;
ll l,r;
int main(){
scanf("%d",&t);
while(t--){
cin>>l>>r;
for(i=63;i>=0;--i) if((l>>i)!=(r>>i)) break; //无需特判,当L=R时,i=-1,结果输出的是0
cout<<(1ll<<(i+1))-1<<endl; 1ll指long long型的1
}
}
起床困难综合症
题目描述
21 世纪,许多人得了一种奇怪的病:起床困难综合症,其临床表现为:起床难,起床后精神不佳。作为一名青春阳光好少年,atm 一直坚持与起床困难综合症作斗争。通过研究相关文献,他找到了该病的发病原因:在深邃的太平洋海底中,出现了一条名为 drd 的巨龙,它掌握着睡眠之精髓,能随意延长大家的睡眠时间。正是由于 drd 的活动,起床困难综合症愈演愈烈,以惊人的速度在世界上传播。为了彻底消灭这种病,atm 决定前往海底,消灭这条恶龙。
历经千辛万苦,atm 终于来到了 drd 所在的地方,准备与其展开艰苦卓绝的战斗。drd 有着十分特殊的技能,他的防御战线能够使用一定的运算来改变他受到的伤害。具体说来,drd 的防御战线由 𝑛 扇防御门组成。每扇防御门包括一个运算 op 和一个参数 𝑡,其中运算一定是 OR,XOR,AND 中的一种,参数则一定为非负整数。如果还未通过防御门时攻击力为 𝑥 ,则其通过这扇防御门后攻击力将变为 𝑥 op 𝑡 。最终drd 受到的伤害为对方初始攻击力 𝑥 依次经过所有 𝒏 扇防御门后转变得到的攻击力。
由于atm 水平有限,他的初始攻击力只能为 0 到 𝑚 之间的一个整数(即他的初始攻击力只能在 0, 1, … , 𝑚 中任选,但在通过防御门之后的攻击力不受 𝑚 的限制)。为了节省体力,他希望通过选择合适的初始攻击力使得他的攻击能让 drd受到最大的伤害,请你帮他计算一下,他的一次攻击最多能使 drd 受到多少伤害
输入描述
第 1 行包含2 个整数,依次为 𝑛, 𝑚 ,表示drd 有 𝑛 扇防御门,atm 的初始攻击力为 0 到 𝑚 之间的整数。
接下来 𝑛 行,依次表示每一扇防御门。每行包括一个字符串 op 和一个非负整数 𝑡,两者由一个空格隔开,且 op 在前, 𝑡 在后,op 表示该防御门所对应的操作,𝑡 表示对应的参数。
输出描述
输出一行一个整数,表示atm 的一次攻击最多使 drd 受到多少伤害
示例一
输入
3 10
AND 5
OR 6
XOR 7
输出
1
说明
atm 可以选择的初始攻击力为 0,1, … ,10。
假设初始攻击力为 4,最终攻击力经过了如下计算
4 AND 5 = 4
4 OR 6 = 6
6 XOR 7 = 1
类似的,我们可以计算出初始攻击力为 1,3,5,7,9 时最终攻击力为 0,初始攻击力为 0,2,4,6,8,10 时最终攻击力为 1,因此atm 的一次攻击最多使 drd 受到的伤害值为 1
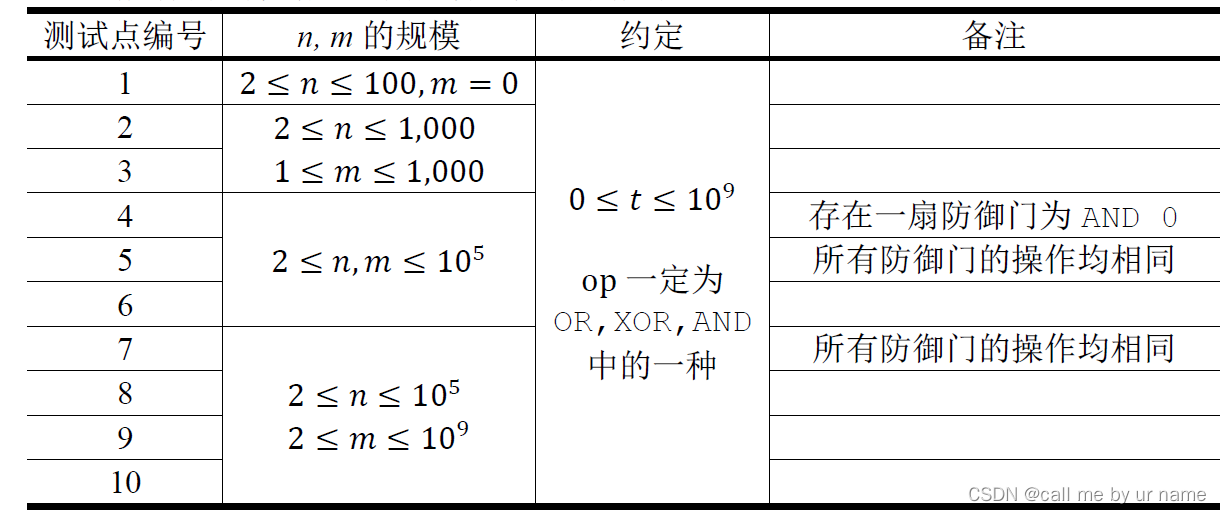
备注
思路
- 首先简化题目的意思——给出初始区间、一段操作符和操作数,由初始区间内的数经过操作后能得到的最大值
- 明显需要使用二进制计算。但如果枚举初始区间内每一个数进行操作,时间复杂度O(mn),可能会TL
- 可以取特殊的数0(0000……)2,-1(111111……)2(都是32位,因为int),当0经过所有的操作后,各个二进制位上是1的位置就应保留(为了让结果最大)。-1经过所有操作后,二进制位上是1的也保留(但是要限制<=m)
题解
#include<bits/stdc++.h>
using namespace std;
int n,m,t,a=0,b=-1,ans=0;
char op[5];
int main(){
scanf("%d%d",&n,&m);
while(n--){
scanf("%s%d",op,&t);
if(op[0]=='A') a&=t,b&=t;
else if(op[0]=='X') a^=t,b^=t;
else a|=t,b|=t;
}
for(int i=1<<29;i;i>>=1){
if(a&i) ans|=i;
else if((b&i)&&(i<=m))ans|=i;
}
printf("%d",ans);
}
总结
- 贪心往往都是细分到每一步都需要进行贪心,从这个思路着手(protecting the flower,每一步 —— 对相邻两个数据进行比较)(矩阵消除游戏,每一步 —— 枚举每一种选择的可能,进行最大值比较)(兔子的区间密码,起床困难综合症,每一步 —— 二进制上获取最多的1)
- 所做的贪心算法不能对后面的贪心选择有影响(矩阵消除游戏,我一开始的WA的方法就违反了这个条例)(按位贪心 —— 二进制的每一位对其他位都没有影响)