前言

当前所有算法都使用测试用例运行过，但是不保证100%的测试用例，如果存在问题务必联系批评指正~

在此感谢左大神让我对算法有了新的感悟认识！

问题介绍

原问题
给定搜索二叉树，将搜索二叉树转为双向链表
如搜索二叉树：
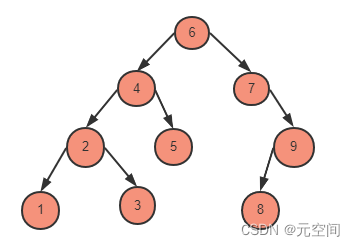
在这里插入图片描述
转化后结果:
1<->2<->3<->4<->5<->6<->7<->8<->9

解决方案

方案一：
1、根据所搜所二叉树特点，中序遍历将节点转化为双向链表节点并放入栈中
2、弹出栈并设置头尾即可
时间 O(n) 空间O(n)
方案二：
1、根据递归的特点，左子树形成部分双向链表，右子树部分形成双向链表，之后将中间节点连接即可
2、注意左边和右边可能没有双向链表的情况

代码编写

java语言版本

public class ChangeTree2LinkList {

    /**
     * 搜索二叉树转双向链表
     * @param root
     * @return
     */
    public static DoubleNode change2TreeNode(MyTreeNode root){
        // 存储头尾的
        DoubleNode[] leftRecord = new DoubleNode[2];
        DoubleNode[] rightRecord = new DoubleNode[2];

        DoubleNode head = null;
        DoubleNode cur = new DoubleNode(root.getData());


        process(root.getLeft(), leftRecord);
        process(root.getRight(), rightRecord);

        if (leftRecord[0] != null){
            head = leftRecord[0];
            leftRecord[1].setNext(cur);
            cur.setLast(leftRecord[1]);
        }
        if (head == null){
            head = cur;
        }
        if (rightRecord[0] != null){
            rightRecord[0].setLast(cur);
            cur.setNext(rightRecord[0]);
        }
        return head;
    }

    private static void process(MyTreeNode root, DoubleNode[] record) {
        if (root == null){
            record[0] = null;
            record[1] = null;
            return;
        }
        DoubleNode head = null;
        DoubleNode tail = null;
        // 自己先变成节点
        DoubleNode doubleNode = new DoubleNode(root.getData());
        if (root.getRight() == null && root.getLeft() == null){
            // 叶子节点
            record[0] = doubleNode;
            record[1] = doubleNode;
            return;
        }
        if (root.getLeft() != null){
            // 左子树递归转链表
            process(root.getLeft(), record);
            if (record[0] != null){
                // 左边有
                head = record[0];
                record[1].setNext(doubleNode);
                doubleNode.setLast(record[1]);
                tail = doubleNode;
            }
        }
        if (head == null){
            head = doubleNode;
        }
        if (root.getRight() != null){
            process(root.getRight(), record);
            if (record[0] != null){
                doubleNode.setNext(record[0]);
                record[0].setLast(doubleNode);
                tail = record[1];
            }
        }
        record[0] = head;
        record[1] = tail;
        return;
    }

    /**
     * 测试用例
     * @param args
     */
    public static void main(String[] args) {
        MyTreeNode myTreeNode6 = new MyTreeNode(6);
        MyTreeNode myTreeNode4 = new MyTreeNode(4);
        MyTreeNode myTreeNode7 = new MyTreeNode(7);
        MyTreeNode myTreeNode2 = new MyTreeNode(2);
        MyTreeNode myTreeNode5 = new MyTreeNode(5);
        MyTreeNode myTreeNode9 = new MyTreeNode(9);
        MyTreeNode myTreeNode1 = new MyTreeNode(1);
        MyTreeNode myTreeNode3 = new MyTreeNode(3);
        MyTreeNode myTreeNode8 = new MyTreeNode(8);
        myTreeNode6.setLeft(myTreeNode4);
        myTreeNode6.setRight(myTreeNode7);
        myTreeNode4.setLeft(myTreeNode2);
        myTreeNode4.setRight(myTreeNode5);
        myTreeNode7.setRight(myTreeNode9);
        myTreeNode2.setLeft(myTreeNode1);
        myTreeNode2.setRight(myTreeNode3);
        myTreeNode9.setLeft(myTreeNode8);
        DoubleNode doubleNode = change2TreeNode(myTreeNode6);
        System.out.println(doubleNode);
    }
}

c语言版本

正在学习中

c++语言版本

正在学习中

思考感悟

1、怎么想到的
方案1：从题目中给的几个关键点出发，首先一定要用到搜索二叉树的特点，中序遍历就是从小到大的正确顺序，那么空间O(n)的办法很容易想到
方案2：从归并算法中可以找到感觉，二叉树很多递归的方式都是将整个问题分解成小的问题来解决，整个双向链表由左半部分（左子树），右半部分（右子树）和中间节点组成，那么就可以递归将左边、中间、右边计算出来进行连接即可
2、关键逻辑
方案二主要注意递归结束条件和树的边界问题
3、拓展问题
递归问题目前有两个角度来思考：
· 递归是将整个大的问题分解成若干个逻辑相同的小问题来解决比如这里的方案二
· 通过递归来遍历栈和取栈底的方法来看，递归存在第二个角度来理解，就是通过递归来进行状态的变化，对特殊的状态进行判断和调整，其他的状态可以不做任何改变，比如获取栈底的方法。