[数据结构与算法]LeetCode 308 周赛

2389. 和有限的最长子序列

题目描述

给你一个长度为 n 的整数数组 nums ，和一个长度为 m 的整数数组 queries 。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是 nums 中 元素之和小于等于 queries[i] 的 子序列 的 最大 长度 。

子序列 是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

示例

输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。

• 1 <= n, m <= 1000

• 1 <= nums[i], queries[i] <= 106

思路

周赛当天的时候，脑子what了。一开始看着这道题，想了半天完全没思路，然后就先跳过了，这可是第一题啊😭当时心态就有点小崩。

结果等到把第2题和第3题都做出来后，还剩了大概半小时，又回头来看这道题，想着用动态规划来做，卡了半天没做出来，一直WA。结果当天到最后也没把这道题给做出来。

不过还是记录一下我错误的思路。我想的是用动态规划，用f[i]来表示只从[0, i]区间中选择子序列，所有子序列中，和不超过该次询问的sum的最长的子序列的长度。

然后分类讨论时，从最后一个位置i，分为选或者不选。进一步分为

• f[i][0]：只从[0, i]区间中选择子序列，且不选择第i个位置，所有子序列中，和不超过sum的最长的子序列的长度
• f[i][1]：只从[0, i]区间中选择子序列，且选择第i个位置，所有子序列中，和不超过sum的最长的子序列的长度

然后我的状态转移方程是：

• 当不选i时，则f[i][0] = max { f[i - 1][0], f[i - 1][1] }
• 当选i时，
  • 需要判断nums[i]是否超过了sum，若超过，则f[i][1] = 0，表示不能选i这个位置；若没超过，则f[i][1]至少为1，纳入这个nums[i]数本身
  • 若f[i - 1][0]的和加上nums[i]没超过sum，则更新f[i][1]
  • 若f[i - 1][1]的和加上nums[i]没超过sum，则更新f[i][1]

最后，对于该次询问的答案则是max { f[n][0], f[n][1] }

class Solution {
    public int[] answerQueries(int[] nums, int[] queries) {
        int n = nums.length, m = queries.length;
        int[] ans = new int[m];
        for (int i = 0; i < m; i++) {
            // 只从前i个位置中考虑子序列, 和不超过sum的最大长度, 0表示第i个位置不选, 1表示第i个位置选
            int[][] f = new int[n + 1][2];
            // 和
            int[][] s = new int[n + 1][2];
            
            int sum = queries[i];
            for (int j = 1; j <= n; j++) {
                if (f[j - 1][0] >= f[j - 1][1]) {
                    f[j][0] = f[j - 1][0];
                    s[j][0] = s[j - 1][0];
                } else {
                    f[j][0] = f[j - 1][1];
                    s[j][0] = s[j - 1][1];
                }
                
                if (nums[j - 1] <= sum) {
                    f[j][1] = 1;
                    s[j][1] = nums[j - 1];
                }
                
                if (s[j - 1][0] + nums[j - 1] <= sum) {
                    f[j][1] = f[j - 1][0] + 1;
                    s[j][1] = s[j - 1][0] + nums[j - 1];
                }
                
                if (s[j - 1][1] + nums[j - 1] <= sum && f[j][1] < f[j - 1][1] + 1) {
                    f[j][1] = f[j - 1][1] + 1;
                    s[j][1] = s[j - 1][1] + nums[j - 1];
                }
            }
            
            ans[i] = Math.max(f[n][0], f[n][1]);
        }
        return ans;
    }
}

这种做法的时间复杂度是$O(nm)$，并不优秀，不过在这道题的数据范围下，$O(nm)$ 也只能达到10^6的级别，并不会超时。

这种思路乍看上去好像是正确的，然而其实是有问题的。我们来看一个错误样例。

输入：
[47,5,63,33,35,75,45]
[81,95]
输出：
[2,3]
预期：
[3,3]

第一个询问的结果就错了，我们把第一个询问对应的状态转移过程输出出来。

f[1][0] = 0, f[1][1] = 1, s[1][0] = 0, s[1][1] = 47
f[2][0] = 1, f[2][1] = 2, s[2][0] = 47, s[2][1] = 52
f[3][0] = 2, f[3][1] = 1, s[3][0] = 52, s[3][1] = 63
f[4][0] = 2, f[4][1] = 1, s[4][0] = 52, s[4][1] = 33
f[5][0] = 2, f[5][1] = 2, s[5][0] = 52, s[5][1] = 68
f[6][0] = 2, f[6][1] = 1, s[6][0] = 52, s[6][1] = 75
f[7][0] = 2, f[7][1] = 1, s[7][0] = 52, s[7][1] = 45

然后我们凭肉眼直接把答案找出来，很明显，子序列[5, 33, 35] 的和为73，是小于81的，其长度是3，所以正确答案应该是3。

对照着看，[5, 33, 35]应该由f[5][1]得来，而实际f[5][1]竟然等于2，我们看看f[5][1]是怎么转移过来的。

按正确的逻辑，f[5][1]（取35）应当由f[4][1]（取33）转移过来，而f[4][1]应当由f[3][0]（不取63）转移来，f[3][0]应当由f[2][1]（取5）转移来。这个状态转移方程是有问题的。每一步都在当前这个位置取得了最大值，但可能会使得后续更小的值无法加上去。

举个极端的例子。

[4,4,4,4,1,1,1,1,1,1,1,1,1,1,1,1]
[16]

f[4][1] = 4，序列为[4,4,4,4] = 16;f[4][0] = 3，序列为[4,4,4] = 12；这是当前能选择的最大长度，并把和尽可能的弄得很大了。

但实际上，如果对于i > 4出现了某一个数字比这个已选定的方案中的某个数字小，则是可以替换掉（可以用1替换掉前面的某个4），并使得长度不变，和变小，便有更大的可能性能容纳更多数字。

所以这种思路是错误的。

正解

这道题是子序列，对于每个数字，都有选或者不选两种选择，子序列的方案数一共是 2^n，要使得子序列的长度尽可能长（尽可能多选），而和又尽可能小。那么一个很直观的感受就是，每次都选一个当前最小的数字。直到选择的数字的和，达到queries[i]，此时无法再选更多的数字进来。那么此时的选择的数字的个数就是最多的。由于只需要从小到大依次选数字，那么数组的顺序就没有什么关系了，故我们可以直接对nums数组从小到大排个序。

一方面，我们想要增加子序列的长度（要选择数字添加进来），另一方面，在<= sum 的限制下，我们希望能添加进来的数字越多越好。那么一个合理的贪心做法就是，每次选择一个数字进来，都选最小的数字，这样能使得和的上升幅度最小，就越能选择更多的数字。

另外，我们稍微证明一下，当从小到大排序后，如果选择了num[i]，则一定要选择全部的[0, i - 1]；

为什么这样呢？用反证法来进行一个说明。若某种方案中，选择了nums[i]，且没有选择nums[k]（k < i），此时方案中所选数字的和为sum，那么一定能够把nums[i]删掉，并添加nums[k]，使得选中的数字个数不变，但是sum变得更小，这样就能有更大的可能容纳更多数字。这是一种贪心的策略。

或者，换个方式来说，对于任意的 $sum={\sum }_0^{i}nums[i]$，<=sum的子序列的选择方案中，长度最大的，一定是选择[0, i]区间中所有的数。

如此以来，我们可以对排序后的nums数组，计算一下前缀和preSum（前缀和单调递增），那么对于一个指定的sum，我们可以找到一个最大的i，使得preSum[i] <= sum，此时[0, i]区间的长度，即是该次询问的答案。

查找这个最大的i的过程，可以用二分来做。所以我们的思路就是：排序+前缀和+二分

（2022/09/06 今天进行总结，重做这道题时，一下子就想到了该种解法，不知道周赛当天为什么脑子what掉了！）

class Solution {
    public int[] answerQueries(int[] nums, int[] queries) {
        int n = nums.length, m = queries.length;
        Arrays.sort(nums);
        for (int i = 1; i < n; i++) nums[i] += nums[i - 1];
        int[] ans = new int[m];
        for (int i = 0; i < m; i++) {
            int l = 0, r = n - 1;
            while (l < r) {
                int mid = l + r + 1 >> 1;
                if (nums[mid] <= queries[i]) l = mid;
                else r = mid - 1;
            }
            // 这里注意加上一个判断, 有可能最小的前缀和都不满足条件
            if (nums[l] <= queries[i]) ans[i] = l + 1;
        }
        return ans;
    }
}

2390. 从字符串中移除星号

题目描述

给你一个包含若干星号 * 的字符串 s 。

在一步操作中，你可以：

• 选中 s 中的一个星号。
• 移除星号 左侧 最近的那个 非星号 字符，并移除该星号自身。

返回移除 所有 星号之后的字符串**。**

注意：

• 生成的输入保证总是可以执行题面中描述的操作。

• 可以证明结果字符串是唯一的。

• 1 <= s.length <= 105

• s 由小写英文字母和星号 * 组成

示例

输入：s = "leet**cod*e"
输出："lecoe"
解释：从左到右执行移除操作：
- 距离第 1 个星号最近的字符是 "leet**cod*e" 中的 't' ，s 变为 "lee*cod*e" 。
- 距离第 2 个星号最近的字符是 "lee*cod*e" 中的 'e' ，s 变为 "lecod*e" 。
- 距离第 3 个星号最近的字符是 "lecod*e" 中的 'd' ，s 变为 "lecoe" 。
不存在其他星号，返回 "lecoe" 。

思路

一个星号可以消除其左侧最近一个非星号的字符，很容易想到用栈。从左往右依次遍历整个字符串，遇到非星号字符，则压栈；遇到星号，则弹出栈顶。

class Solution {
    public String removeStars(String s) {
        int n = s.length();
        char[] stack = new char[n];
        int top = -1;
        for (int i = 0; i < n; i++) {
            char c = s.charAt(i);
            if (c != '*') stack[++top] = c;
            else if (top >= 0) top--; // 是星号, 并且前面有字母字符, 则弹出
        }
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i <= top; i++) sb.append(stack[i]);
        return sb.toString();
    }
}

2391. 收集垃圾的最少总时间

题目描述

给你一个下标从 0 开始的字符串数组 garbage ，其中 garbage[i] 表示第 i 个房子的垃圾集合。garbage[i] 只包含字符 'M' ，'P' 和 'G' ，但可能包含多个相同字符，每个字符分别表示一单位的金属、纸和玻璃。垃圾车收拾 一 单位的任何一种垃圾都需要花费 1 分钟。

同时给你一个下标从 0 开始的整数数组 travel ，其中 travel[i] 是垃圾车从房子 i 行驶到房子 i + 1 需要的分钟数。

城市里总共有三辆垃圾车，分别收拾三种垃圾。每辆垃圾车都从房子 0 出发，按顺序 到达每一栋房子。但它们 不是必须 到达所有的房子。

任何时刻只有 一辆 垃圾车处在使用状态。当一辆垃圾车在行驶或者收拾垃圾的时候，另外两辆车 不能 做任何事情。

请你返回收拾完所有垃圾需要花费的 最少 总分钟数。

示例

输入：garbage = ["MMM","PGM","GP"], travel = [3,10]
输出：37
解释：
收拾金属的垃圾车花费 7 分钟收拾完所有的金属垃圾。
收拾纸的垃圾车花费 15 分钟收拾完所有的纸垃圾。
收拾玻璃的垃圾车花费 15 分钟收拾完所有的玻璃垃圾。
总共花费 7 + 15 + 15 = 37 分钟收拾完所有的垃圾。

思路

简单题，收拾P的垃圾车，需要从第一个位置，行驶到最后一个包含P的位置，行驶时间根据travel数组算出来，收集的时间就是P出现的次数。对于其他两种类型的垃圾，同理。则我们只需要维护，每种垃圾出现的次数，以及最后出现该种垃圾的位置，然后进行累加计算即可。

class Solution {
    public int garbageCollection(String[] garbage, int[] travel) {
        int pNum = 0, mNum = 0, gNum = 0;
        int pPos = 0, mPos = 0, gPos = 0;
        int[] preSum = new int[travel.length + 1];
        for (int i = 1; i <= travel.length; i++) preSum[i] = preSum[i - 1] + travel[i - 1];
        for (int j = 0; j < garbage.length; j++) {
            String s = garbage[j];
            for (int i = 0; i < s.length(); i++) {
                char c = s.charAt(i);
                if (c == 'P') {
                    pNum++;
                    pPos = j;
                } else if (c == 'G') {
                    gNum++;
                    gPos = j;
                } else {
                    mNum++;
                    mPos = j;
                }
            }
        }
        return pNum + mNum + gNum + preSum[pPos] + preSum[gPos] + preSum[mPos];
    }
}

2392.给定条件下构造矩阵

题目描述

给你一个 正 整数 k ，同时给你：

• 一个大小为 n 的二维整数数组 rowConditions ，其中 rowConditions[i] = [abovei, belowi] 和
• 一个大小为 m 的二维整数数组 colConditions ，其中 colConditions[i] = [lefti, righti] 。

两个数组里的整数都是 1 到 k 之间的数字。

你需要构造一个 k x k 的矩阵，1 到 k 每个数字需要 恰好出现一次 。剩余的数字都是 0 。

矩阵还需要满足以下条件：

• 对于所有 0 到 n - 1 之间的下标 i ，数字 abovei 所在的 行 必须在数字 belowi 所在行的上面。
• 对于所有 0 到 m - 1 之间的下标 i ，数字 lefti 所在的 列 必须在数字 righti 所在列的左边。

返回满足上述要求的 任意 矩阵。如果不存在答案，返回一个空的矩阵。

示例

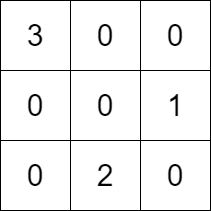
输入：k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]
输出：[[3,0,0],[0,0,1],[0,2,0]]
解释：上图为一个符合所有条件的矩阵。
行要求如下：
- 数字 1 在第 1 行，数字 2 在第 2 行，1 在 2 的上面。
- 数字 3 在第 0 行，数字 2 在第 2 行，3 在 2 的上面。
列要求如下：
- 数字 2 在第 1 列，数字 1 在第 2 列，2 在 1 的左边。
- 数字 3 在第 0 列，数字 2 在第 1 列，3 在 2 的左边。
注意，可能有多种正确的答案。

思路

经过仔细读题，和自己针对一些样例数据进行模拟，容易发现，其实rowCondition和colCondition就是一个依赖关系。

比如：rowConditions = [[1,2],[3,2]]，那么1在2上面，3在2上面。我们用箭头来表示这种上下的关系，即是

1 -> 2,  3 -> 2

我们需要对这些数在行上从上到下进行排列，保证箭头左边的数都在上面，箭头右边的数都在下面。

那么排在第一行的数，一定没有任何箭头指向它（一定没有任何数在它上面）。而是否有箭头指向自己，我们可以想到用图中的入度的概念来表示。那么放在第一行的数字，其入度一定是0；据此，我们容易想到，这道题其实就是个拓扑排序；根据行上和列上的约束关系，可以建立起图，我们对图中的每个点统计起入度，然后按照拓扑排序的规则，先在行上从上到下排序，再在列上从左到右排序即可。

但这道题还需要判断是否存在拓扑序（当不存在拓扑序时，则是不存在满足约束的有效答案，此时图中一定存在环）。

我周赛当晚没有机会和这道题打照面。今天重新来做时，能想到拓扑排序这一点。但是对于如何判断是否存在有效答案这一点，我想的比较复杂了。

我初步的想法是，通过维护点与点之间的父子关系，在每次读入一组新的约束时，判断这组约束是否和先前的约束有冲突，若有，则说明不存在答案。（其实就是判断图中是否存在环）

我下面的写法通过维护父子关系的两个Map来判断是否存在环。（这个父子关系的维护有点问题）

class Solution {
    public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {
        Map<Integer, Set<Integer>> parents = new HashMap<>();
        Map<Integer, List<Integer>> descendants = new HashMap<>();
        int[] rowInDegree = new int[k + 1]; // 在行上的入度
        int[] colInDegree = new int[k + 1]; // 在列上的入度
        // 拓扑排序
        // 先处理行, 如果约束有矛盾则提前退出即可
        for (int[] r : rowConditions) {
            int above = r[0], below = r[1];
            // 与先前的约束有冲突, 存在环, 则直接结束
            if (parents.containsKey(above) && parents.get(above).contains(below)) {
                return new int[0][0];
            }
            if (!parents.containsKey(below)) parents.put(below, new HashSet<>());
            if (!descendants.containsKey(above)) descendants.put(above, new ArrayList<>());
            parents.get(below).add(above);
            descendants.get(above).add(below);
            rowInDegree[below]++; // 下面的入度+1
        }
        // 拓扑排序
        // 每个数字所在的行
        int[] rowIndex = new int[k + 1];
        Queue<Integer> q = new LinkedList<>();
        // 入度为0的点
        for (int i = 1; i <= k; i++) {
            if (rowInDegree[i] == 0) q.offer(i);
        }
        int it = 0; //
        while (!q.isEmpty()) {
            int x = q.poll();
            rowIndex[x] = it++;
            List<Integer> sons = descendants.get(x);
            if (sons == null) continue;
            for (int s : sons) {
                if (--rowInDegree[s] == 0) q.offer(s);
            }
        }

        parents.clear();
        descendants.clear();

        for (int[] c : colConditions) {
            int left = c[0], right = c[1];
            if (parents.containsKey(left) && parents.get(left).contains(right)) {
                return new int[0][0];
            }
            if (!parents.containsKey(right)) parents.put(right, new HashSet<>());
            if (!descendants.containsKey(left)) descendants.put(left, new ArrayList<>());
            parents.get(right).add(left);
            descendants.get(left).add(right);
            colInDegree[right]++;
        }

        q.clear();
        for (int i = 1; i <= k; i++) {
            if (colInDegree[i] == 0) q.offer(i);
        }
        it = 0;
        int[] colIndex = new int[k + 1];
        while (!q.isEmpty()) {
            int x = q.poll();
            colIndex[x] = it++;
            List<Integer> sons = descendants.get(x);
            if (sons == null) continue;
            for (int s : sons) {
                if (--colInDegree[s] == 0) q.offer(s);
            }
        }

        int[][] ans = new int[k][k];
        for (int i = 1; i <= k; i++) {
            int r = rowIndex[i], c = colIndex[i];
            ans[r][c] = i;
        }

        return ans;
    }
}

实际上，判断一个图是否有环，直接用拓扑排序就可以了。拓扑排序的每一轮，我们会从图中删除一个当前入度为0的点，然后对其所有出边的点的入度减1。如果拓扑排序结束后，图中还有未被删除的点，则说明存在环。

class Solution {
    public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {
        // 实际上是每一行放一个数字, 每一列放一个数字, 有点类似N皇后问题
        int[] row = topSort(k, rowConditions);
        int[] col = topSort(k, colConditions);
        if (row.length < k || col.length < k) return new int[0][0];
        int[][] ans = new int[k][k];
        int[] t = new int[k + 1];
        // 记录某个数字在某一行出现
        for (int i = 0; i < k; i++) t[row[i]] = i;
        for (int i = 0; i < k; i++) ans[t[col[i]]][i] = col[i];
        return ans;
    }

    private int[] topSort(int k, int[][] conditions) {
        int[] inDegree = new int[k + 1];
        Map<Integer, List<Integer>> map = new HashMap<>();
        for (int[] c : conditions) {
            int a = c[0], b = c[1];
            if (!map.containsKey(a)) map.put(a, new LinkedList<>());
            map.get(a).add(b);
            inDegree[b]++;
        }
        int[] q = new int[k];
        int hh = 0, tt = -1;
        for (int i = 1; i <= k; i++) {
            if (inDegree[i] == 0) q[++tt] = i;
        }
        while (tt >= hh) {
            int x = q[hh++];
            List<Integer> next = map.get(x);
            if (next == null) continue;
            for (int i : next) {
                if (--inDegree[i] == 0) q[++tt] = i;
            }
        }
        int[] ret = new int[tt + 1];
        for (int i = 0; i <= tt; i++) ret[i] = q[i];
        return ret;
    }
}

总结

本场周赛成绩很糟糕，第一题没写出。下次还得继续加油。