递归
函数调用自身的过程成为递归,调用自身函数称为递归函数,用递归方式解决问题的算法称为递归算法。
- 函数调用自身的实现方式
- 直接调用自身
int funciton(/*...*/) {
//......
//调用自身
function(/*...*/);
//......
}
- 间接调用自身
int funciton(/*...*/) {
//......
//调用自身
function(/*...*/);
//......
}
//function1() 函数内部调用了 function2() 函数,而 function2() 函数内部又调用了 function1() 函数。也就是说,function1() 函数间接调用了自身
- 递归求n!
long long funMul(long long n)
{
if (n == 1 || n == 0)return 1;
return n * funMul(n - 1);
}
int main()
{
int n ;
cin >> n;
cout << funMul(n) << endl;
return 0;
}
递归底层实现机制
-
当一个函数直接或间接调用自身时,称这个函数为调用者,将直接或间接调用的自身称为被调用者
-
递归函数执行时,调用者会将执行代码的权力移交给被调用者,同时还可能会向被调用者传输一些数据。此后,调用者将暂停执行,直至被调用者执行完成并将执行代码的权力交换给调用者后,它才能继续执行。
-
为了确保调用者能够从暂停状态继续执行,当发生递归调用时,多数编程语言都使用栈结构保存调用者的状态信息,包括暂停时局部变量的值、寄存器中保存的数据等等。
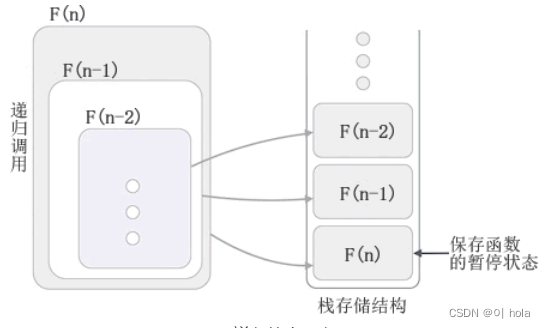
F(n) 调用了 F(n-1),因此 F(n) 会暂停执行,将执行代码的权力移交给 F(n-1),F(n) 的暂停状态也会入栈保存;同样的道理,F(n-1) 中调用了 F(n-2),所以 F(n-1) 暂停执行,暂停状态入栈保存,执行代码的权力移交给 F(n-2)…直至递归停止,执行代码的权力会移交给栈中最顶部的函数,该函数的暂停状态信息会从栈中取出并恢复,该函数继续执行,执行完成后再将执行权力移交给栈顶的函数。直至 F(n) 出栈并执行完成,整个递归过程才算完成
分治策略
-
大规模的问题–> 划分成相同的小规模的问题
-
先将整个问题拆分成多个相互独立且数据量更少的小问题,通过逐一解决这些简单的小问题,最终找到解决整个问题的方案
-
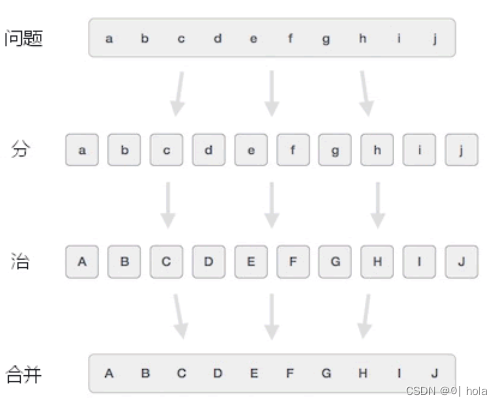
分治策略解决步骤
- 分:将整个问题划分成多个相对独立、涉及数据量更少的小问题,有些小问题还可以划分成很多更小的问题,直至每个问题都不可再分;
- 治:逐个解决所有小问题
- 合并:将所有小问题的解决方案合并到一起,找到整个问题的方案
- 分治策略的优缺点
- 优点: 小问题之间是相互独立的,处理次序不分先后,因此可以采用“并行”的方式让计算机同时处理多个小问题,提高问题的解决效率
- 缺点: 需要与递归算法搭配使用,会耗费大量的时间和内存空间
求数组的最大值和最小值
分治算法与二分查找结合
int Get_Max(int* arr, int left, int right)
{
if (arr == nullptr)return -1;
if (right - left == 0)return arr[left]; //数组中只有一个元素
if (right - left <= 1) //数组中有两个数字
{
return arr[left] >= arr[right] ? arr[left] : arr[right];
}
int mid = (right - left) / 2 + left; //找到中间的元素
int max_leftmid = Get_Max(arr, left, mid); //得到左边最大值
int max_rightmid = Get_Max(arr, mid + 1, right); //得到右边最大值
return max_leftmid >= max_rightmid ? max_leftmid : max_rightmid; //比较 得到整个区域的最大值
}
int Get_Min(int* arr, int left, int right) //有错误 输出结果错误
{
if (arr == nullptr)return -1;
if (right - left == 0)return arr[left];
if (right - left <= 1)
{
return arr[left] <= arr[right] ? arr[left] : arr[right];
}
int mid = (right - left) / 2 + left;
int min_leftmid = Get_Min(arr, left, mid);
int min_rightmid = Get_Min(arr, mid + 1, right);
return min_leftmid <= min_rightmid ? min_leftmid : min_rightmid;
}
int main()
{
int n[2] = {};
int len = sizeof(n) / sizeof(n[0]);
cout << "输入"<<len<<"个数组元素:" ;
for (int i = 0; i < len; ++i)
{
cin >> n[i];
}
cout << "最大值为:" << Get_Max(n, 0, len) << endl;
cout << "最小值为:" << Get_Min(n, 0, len) << endl;
return 0;
}
动态规划
-
Dynamic Programming (DP)
-
求一个问题的最优解(最大值或最小值),而且该问题能够分解成若干个子问题,并且子问题之间还有重叠的更小的子问题,则可以考虑动态规划求解问题。
-
特点
| 特点 | 例题分析 |
|---|---|
| 1. 问题的目标是求一个问题的最优解(最大值或最小值) | – 长度为n的绳子剪成若干段,求各段长度乘积最大 |
| 2. 整体问题的最优解是依赖各子问题的最优解 | – 第一刀剪在长度为i的位置,则剪出来的长度分别为i和n-i的两段。我们要想得到整个问题的最优解fn),那么要同样用最优化的方法把长度为i和n-i的两段分别剪成若干段,使得它们各自剪出的每段绳子的长度乘积最大。 |
| 3. 把大问题分解成若干个子问题,这些子问题之间有相互重叠的更小的子问题 | – 假设绳子最初的长度为10,我们可以把绳子剪成长度分别为4和6的两段,也就是f(4)和f(6)都是f(10)的子问题。接下来分别求解这两个子问题。我们可以把长度为4的绳子剪成均为2的两段,即f(2)是f4)的子问题。同样,我们也可以把长度为6的绳子剪成长度分别为2和4的两段,即f(2)和f(4)都是f(6)的子问题。我们注意到f(2)是f(4)和f(6)公共的更小的子问题。 |
| 4. 从上往下分析问题,从下往上求解问题 | – 从解决最小问题开始,把以解决的子问题的最优解存储下来(一维或二维数组中),并把子问题的最优解组合起来逐步解决大的问题 |
- 五大步骤
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
- 剪绳子问题
/*
剪绳子:长度为n的绳子,剪成m段,每段绳子的长度k[0],k[1],..k[m], (n>1,m>1)
求解k[0]xk[1]xk[2]...可能的最大乘积是多少? f(n)表示长度为n的剪完后的乘积最大值
第一刀 可能的长度为1,2,,,n-1, 递归公式: f(n)=max(f(i)*f(n-i)
绳子长度为2时,剪成两端为1,则f(2)=1;
绳子长度为3时,剪成两端为1,2;或者长度为1,1,1,三段,则f(3)=2;
*/
int MaxCutting(int len)
{
if (len < 2) return 0;
if (len == 2)return 1;
if (len == 3)return 2;
int* product = new int[len + 1];
//数组存放最优解 第i个元素表示吧长度i的绳子剪成若干段后长度乘积的最大值 f(i)
product[0] = 0;
product[1] = 1;
product[2] = 2;
product[3] = 3;
int max = 0;
for (int i = 4; i <= len; ++i) //顺序递增 自下而上
{
max = 0;
for (int j = 1; j <= i / 2; ++j) //只需要找到i/2处,之后的组合都是前面计算过的
{
int pro = product[j] * product[i - j];
if (max < pro) max = pro;
product[i] = max; //每次计算完有比上次更优解的 就保存在product中
}
}
max = product[len];
delete[]product;
return max;
}
int main()
{
cout << "输入绳子长度: ";
int n = 0;
cin >> n;
cout << MaxCutting(n) << endl;
return 0;
}
- 斐波那契数列
/*
斐波那契数列:后一项等于前n-1项加上前n-2项
1,1,2,3,5...
*/
int Fibonacci(int n)
//时间复杂度:O(n) 空间复杂度: O(n)
int fib(int N) {
if (N <= 1) return N;
vector<int> dp(N + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[N];
}
//时间复杂度:O(n) 空间复杂度: O(1)
int fib_2(int N) {
if (N <= 1) return N;
int dp[2];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
int sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return dp[1];
}
//递归 时间复杂度:O(2^n) 空间复杂度:O(n)
int fib_3(int N) {
if (N < 2) return N;
return fib(N - 1) + fib(N - 2);
}
int main()
{
for (int i = 0; i < 5; i++)
{
cout << fib(i) << " ";
}
cout << endl;
return 0;
}
- 青蛙跳台阶问题
/*
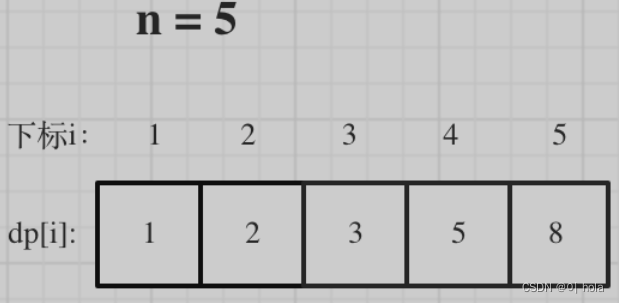
跳台阶问题:
1.一只青蛙一次可以跳上1级台阶,也可以跳上2级,
找出规律
先跳一层,子问题变为求 f(n-1)个跳法
先跳两层,子问题变为求f(n-2)个跳法
第n层 :f(n)=f(n-1)+f(n-2)
*/
int climbStairs(int n) {
if (n <= 1) return n; // 因为下面直接对dp[2]操作了,防止空指针
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) { // 注意i是从3开始的
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
int climbStairs_2(int n) {
if (n <= 1) return n;
int dp[3];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
return dp[2];
}
int Jump_1(int n) //一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法
{
if (n == 0) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
return Jump_1(n - 1) + Jump_1(n - 2);
}
int Jump_2(int n) //一只青蛙一次可以跳上1级台阶,也可以跳上2级,也可以跳上n阶,求该青蛙跳上一个 n 级的台阶总共有多少种跳法
{
if (n == 0)return 0;
if (n == 1) return 1;
return 2 * Jump_2(n - 1);
}
int main()
{
int n = 0;
cin >> n;
cout << Jump_1(n) << endl;
return 0;
}
- 最小花费爬梯子
/*
数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
*/
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size());
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < cost.size(); i++) {
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
}
// 注意最后一步可以理解为不用花费,所以取倒数第一步,第二步的最少值
return min(dp[cost.size() - 1], dp[cost.size() - 2]);
}
- 不同路径

/*
不同路径:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
1.确定dp数组及下标yiyi
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2.确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来
3.dp、数组初始化
dp[i][0]==1,dp[0][j]==1
for(int i=0;i<m;i++) dp[i][0] = 1;
for(int j=0;i<n;j++) dp[0][j] = 1;
4.确定遍历顺序
从左到右一层一层
*/
//时间复杂度:O(m*n) 空间复杂度:O(m*n) 二维
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
//时间复杂度:O(m*n) 空间复杂度:O(n) 一维
int uniquePaths_2(int m, int n) {
vector<int> dp(n);
for (int i = 0; i < n; i++) dp[i] = 1;
for (int j = 1; j < m; j++) {
for (int i = 1; i < n; i++) {
dp[i] += dp[i - 1];
}
}
return dp[n - 1];
}
int main()
{
cout << uniquePaths(3, 7)<<endl;
return 0;
}
- 不同路径 II
 对应的dp表如下:
对应的dp表如下:
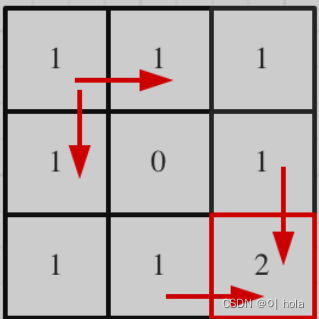
- 确定dp数组及下标含义
dp[i][j]:表示从(0,0)到(i,j)有dp[i][j]条不同路径 - 确定递推公式
if(obstacle[i][j] ==0) { dp[i][j] = dp[i-1][j]+dp[i][j-1] }
当有障碍的话就要保持初始状态,没有障碍在进行相加
- dp数组初始化
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
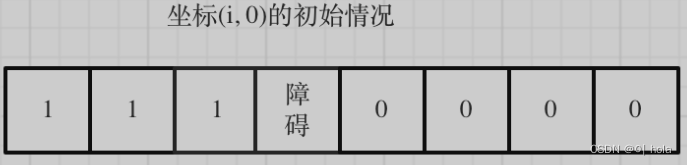
- 确定遍历顺序
从左到右一层一层遍历
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacle[i][j] == 0)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
/*
不同路径II:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
传入障碍二维数组vector<vector<int>>
*/
int uniquePath(vector<vector<int>>& obstacle)
{
int m = obstacle.size();
int n = obstacle[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacle[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacle[0][j] == 0; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++)
{
for (int j = 1; j < n; j++)
{
if (obstacle[i][j] == 0)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
int main()
{
vector<vector<int>> obs{ {0,0,0},{0,1,0},{0,0,0} };
cout << uniquePath(obs) << endl;
return 0;
}
- 整数拆分
- 确定dp数组及含义
dp[i]:表示拆分数字i,能够或得的最大乘积为dp[i] - 确定递推公式
其实可以从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。j * (i - j) 是单纯的把整数拆分为两个数相乘
一个是j * dp[i - j],相当于是拆分(i - j),j * dp[i - j]是拆分成两个以及两个以上的个数相乘。
递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j}); - dp数组初始化
dp[2] = 1 - 遍历顺序
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
枚举j的时候,是从1开始的。i是从3开始,这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。
for (int i = 3; i <= n ; i++) {
for (int j = 1; j < i - 1; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}

/*
整数拆分:给定一个正整数n,将其拆分为至少两个正整数的和,病史这些整数的乘积最大化。返回最大乘积
*/
int GetMultiNum(int n)
{
vector<int> dp(n + 1);
dp[2] = 1;
for (int i = 3; i <= n; i++)
{
for (int j = 1; j < i - 1; j++)
{
dp[i] = max(dp[i], max(dp[i - j] * j, (i - j) * j));
}
}
return dp[n];
}
int main()
{
cout << GetMultiNum(10) << endl;
return 0;
}
- 不同的二叉搜索树

推导:
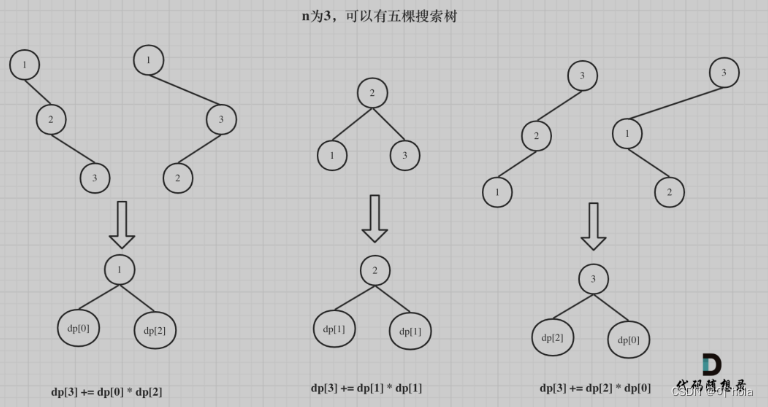
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
- 确定dp数组及含义
dp[i]:表示1到i为结点组成的二叉搜索树的个数 - 确定递推公式
递推关系, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止
递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量 - 数组初始化
dp[0]=1
dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,
也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。 - 确定遍历顺序
节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i里面每一个数作为头结点的状态,用j来遍历。 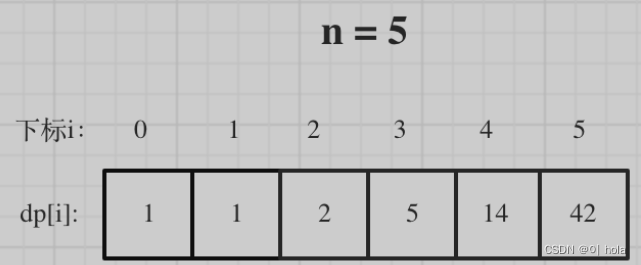
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
/*
不同的二叉搜索树:给定整数n,求以1,2,..n为节点组成的二叉搜索树有多少种
每个节点的左孩子都小于它,右孩子都大于它
*/
int TreesNum(int n)
{
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= i; j++)
{
dp[i] += dp[j - 1] + dp[i - j];
}
}
return dp[n];
}
int main()
{
cout << TreesNum(5) << endl;
return 0;
}