[数据结构与算法]动态规划 - 路径总数 & 最小路径和

目录

1.路径总数

1.1 题目描述

?1.2 思路分析

1.3 代码示例

2.最小路径和

2.1 题目描述

2.2 思路分析

2.3 代码示例

1.路径总数

1.1 题目描述

一个机器人在m×n大小的地图的左上角（起点）。
机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。
可以有多少种不同的路径从起点走到终点？

备注：m和n小于等于100,并保证计算结果在int范围内

数据范围：0 < n,m \le 1000<n,m≤100，保证计算结果在32位整型范围内
要求：空间复杂度 O(nm)O(nm)，时间复杂度 O(nm)O(nm)
进阶：空间复杂度 O(1)O(1)，时间复杂度 O(min(n,m))O(min(n,m))

?1.2 思路分析

?

问题：从起点到终点的路径总数

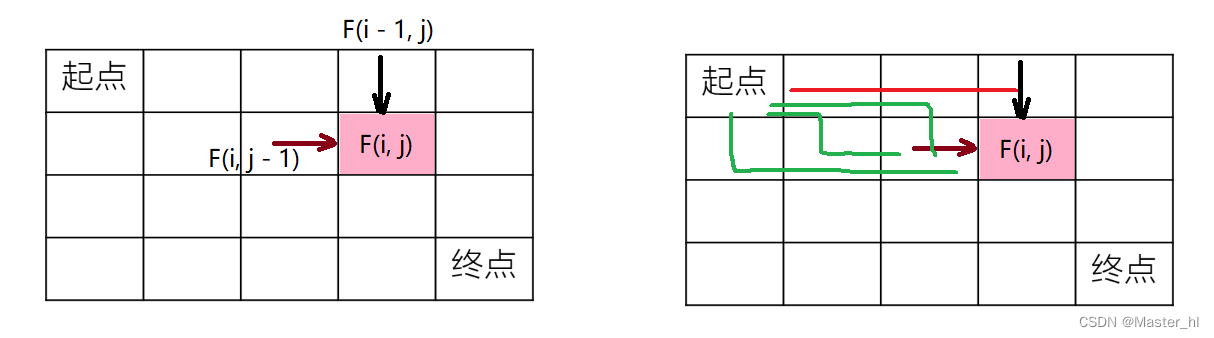
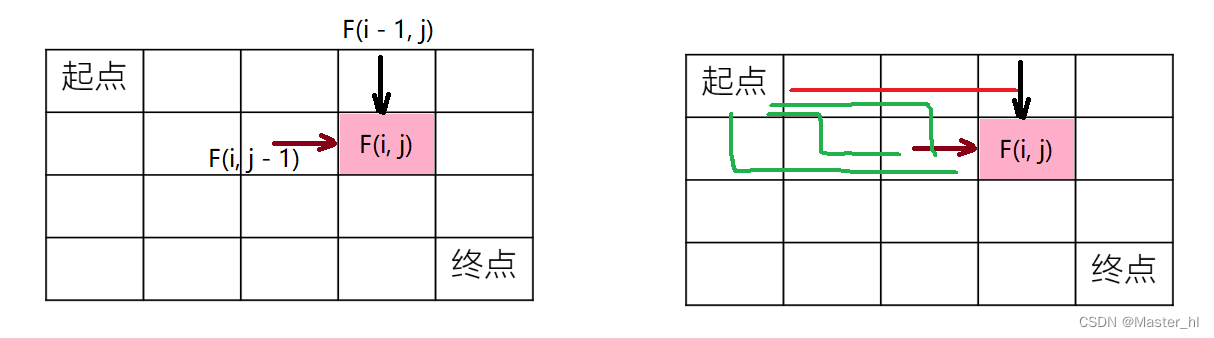
状态 F(i, j)：从 (0, 0) 到 (i, j) 的路径总数

状态转移方程：F(i, j) = F(i - 1, j) + F(i, j - 1)；

初始状态：F(i, 0) = F(0, j) = 1

第一行和第一列的每个点的路径数都只有一条，因为机器人只能向右和向下走；

返回结果：F(i, j)

1.3 代码示例

public class Solution {
    public int uniquePaths (int m, int n) {
        if(m == 0 || n == 0) {
            return 0;
        }
        // 初始状态 - 第一列每个点的路径数都为 1
        int[][] array = new int[m][n];
        for(int i = 0; i < m; i++) {
            array[i][0] = 1;
        }
        // 初始状态 - 第一行每个点的路径数都为 1
        for(int j = 0; j < n; j++) {
            array[0][j] = 1;
        }
        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                // 状态转移方程
                array[i][j] = array[i][j - 1] + array[i - 1][j];
            }
        }
        // 返回最后一个点的路径数
        return array[m - 1][n - 1];
    }
}

2.最小路径和

2.1 题目描述

给定一个由非负整数填充的m x n的二维数组，现在要从二维数组的左上角走到右下角，
请找出路径上的所有数字之和最小的路径。
注意：你每次只能向下或向右移动。

2.2 思路分析

问题：从起点到终点的所有路径中数字之和最小的路径

状态 F(i, j)： 从 (0, 0) 到 (i, j) 的最小路径和

状态转移方程：

• i == 0? && j != 0? ? ? ?F(0, j) = F(0, j - 1) + F(0, j)
• j == 0 && i != 0? ? ? ? F(i, 0) = F(i - 1, 0) + F(i, 0)
• i != 0 && j != 0? ? ? ? ?F(i, j) = min(F(i, j - 1), F(i - 1, j)) + F(i, j)

初始状态：F(0, 0)? = array[0][0]

返回结果：F(i, j)

2.3 代码示例

写法一：

public class Solution {
    public int minPathSum (int[][] grid) {
        if(grid == null || grid.length == 0) {
            return 0;
        }
        int row = grid.length;
        int col = grid[0].length;
        // 初始状态: F(0,0) = grid[0][0]
        // 第一列的最小路径和
        for(int i = 1; i < row; i++) {
            grid[i][0] = grid[i - 1][0] + grid[i][0];
        }
        // 第一行的最小路径和
        for(int j = 1; j < col; j++) {
            grid[0][j] = grid[0][j - 1] + grid[0][j];
        }
        // 状态转移方程
        for(int i = 1; i < row; i++) {
            for(int j = 1; j < col; j++) {
                grid[i][j] = Math.min(grid[i][j -1],grid[i - 1][j]) + grid[i][j];
            }
        }
        return grid[row - 1][col - 1];
    }
}

写法二：

public class Solution {
    public int minPathSum (int[][] grid) {
        if(grid == null || grid.length == 0) {
            return 0;
        }
        int row = grid.length;
        int col = grid[0].length;
        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                // 状态转移方程
                if(i == 0 && j != 0) {
                    grid[0][j] = grid[0][j - 1] + grid[0][j];
                } else if(j == 0 && i != 0) {
                    grid[i][0] = grid[i - 1][0] + grid[i][0];
                } else if(i != 0 && j != 0) {
                    grid[i][j] = Math.min(grid[i - 1][j], grid[i][j - 1])
                        + grid[i][j];
                }
            }
        }
        return grid[row - 1][col - 1];
    }
}

谢谢观看！！