如何理解深度优先算法
深度优先算法:就是类似于树的遍历!!!
回溯:就是比如先序遍历后左节点后,当左节点优先遍历完成后,返回到父节点遍历父节点的右边
见枝:就是遍历左节点后返回的信息告诉父节点,不需要再遍历右节点了
具体:我们就看下面的例题以及视频!!!
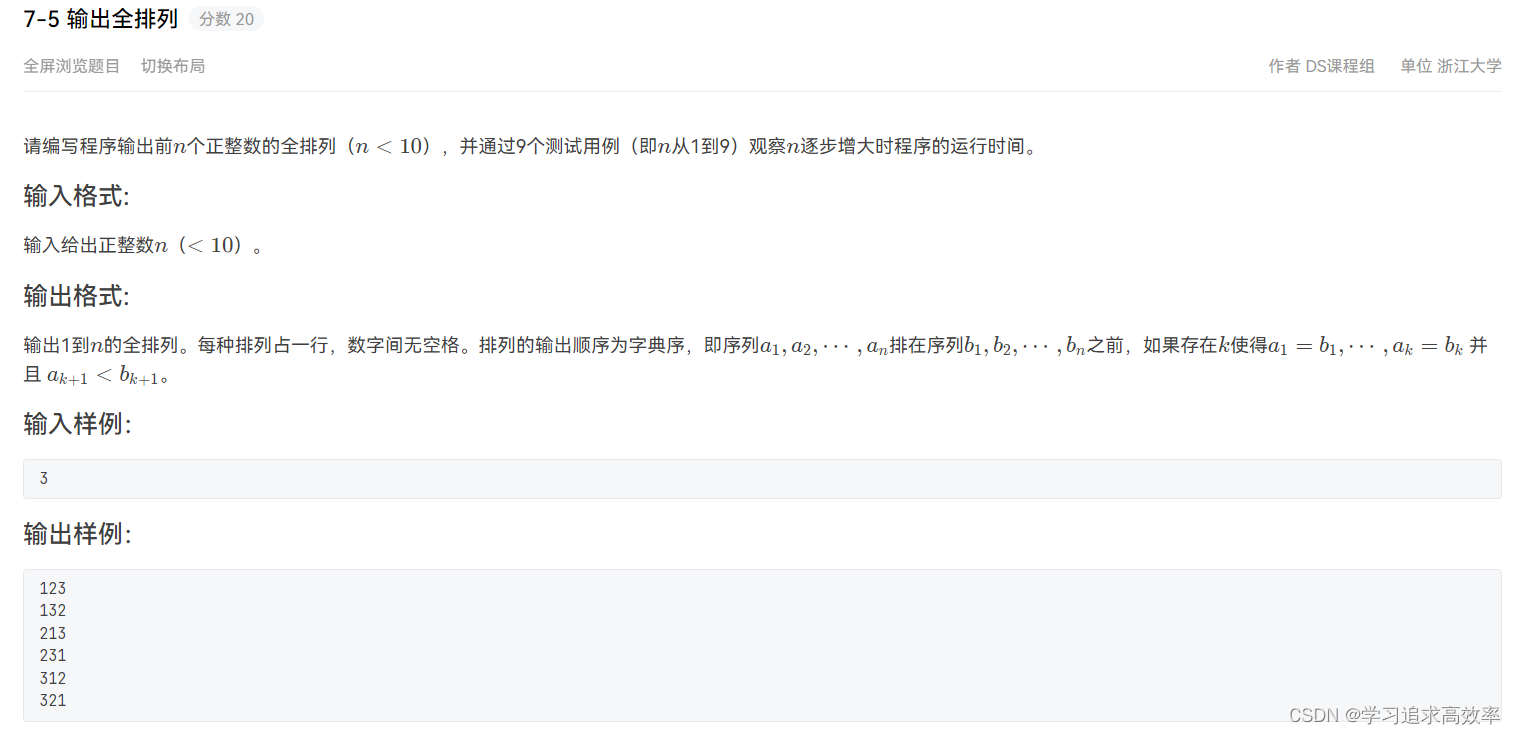
7-5 输出全排列
#include<iostream>
using namespace std;
int n;
int a[10];
bool b[10];
void dfs(int j)
{
if(j == n)
{
for(int i = 0; i < n; i++)
{
cout << a[i];
if(i == n - 1)
cout << endl;
}
return;
}
for(int i = 1; i <= n; i++)
{
if(b[i] == false)
{
a[j++] = i;
b[i] = true;
dfs(j);
b[i] = false;
j--;
}
}
}
int main()
{
cin >> n;
dfs(0);
return 0;
}
注意:本体dfs递归传送的数据是 数组的角标
也就是一个dfs中的循环针对的是一个数据角标
注意下一题,dfs传入的数据是,数组的数值,也就是dfs中一个循环,循环的是数组的角标,而角标对应的数值是dfs的参数
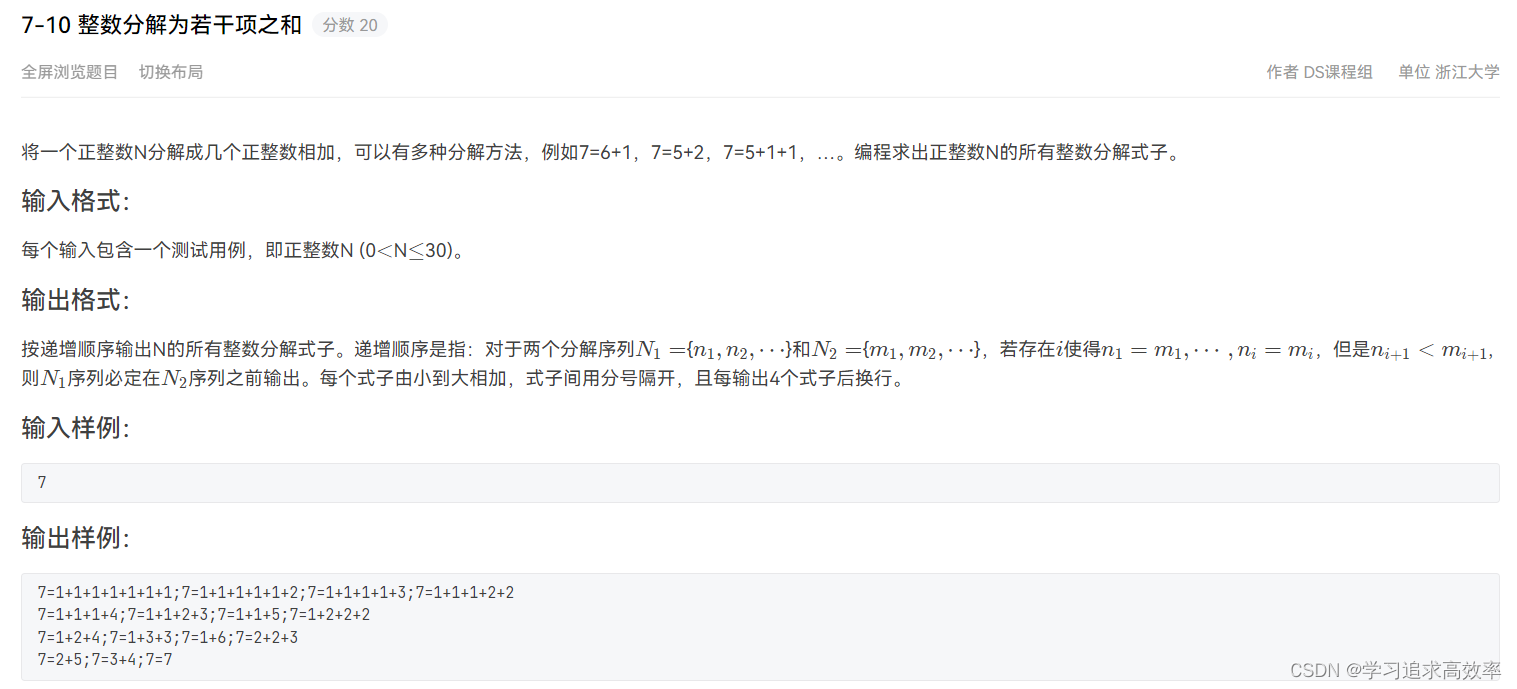
7-10 整数分解为若干项之和
#include<iostream>
using namespace std;
int a[31];
int sum;
int n;
int j;
void dfs(int s)
{
if (sum == n)
{
for (int i = 0; i < j; i++)
cout << a[i];
cout << endl;
return;
}
if(sum>n)
{
return;
}
for (int i = s; i <= n; i++)
{
a[j++] = i;
sum += i;
dfs(i);
sum -= i;
j--;
}
}
int main()
{
cin >> n;
dfs(1);
return 0;
}
如何理解 dfs就是树的遍历
以第一题为例,第一题的遍历过程,类似于如下
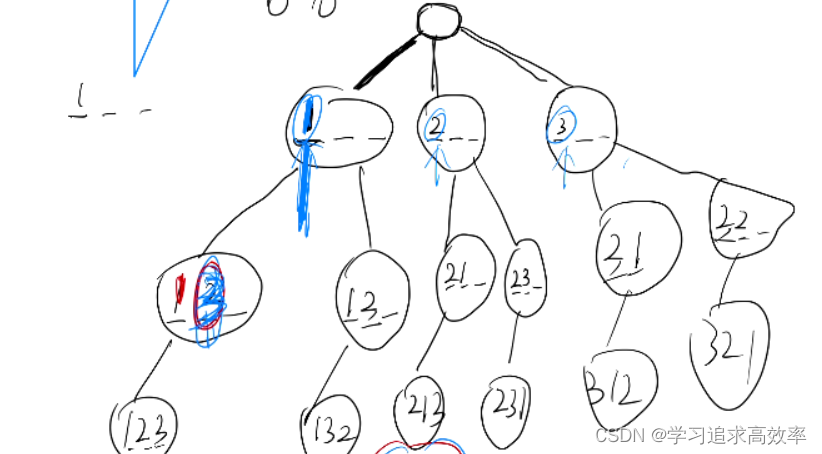
就是先序遍历,然后走不通后,就递归回来