IT数码 购物 网址 头条 软件 日历 阅读 图书馆
TxT小说阅读器
↓语音阅读,小说下载,古典文学↓ 		图片批量下载器
↓批量下载图片,美女图库↓ 		图片自动播放器
↓图片自动播放器↓ 		一键清除垃圾
↓轻轻一点,清除系统垃圾↓
开发: C++知识库 Java知识库 JavaScript Python PHP知识库 人工智能 区块链 大数据 移动开发 嵌入式 开发工具 数据结构与算法 开发测试 游戏开发 网络协议 系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑 笔记本 显卡 显示器 固态硬盘 硬盘 耳机 手机 iphone vivo oppo 小米 华为 单反 装机 图拉丁
 
   -> 数据结构与算法 -> 二叉树简介 -> 正文阅读

[数据结构与算法]二叉树简介

二叉树

(一)二叉树简介

1.线性结构与非线性结构

线性结构：数组、链表、栈、队列
非线性结构：二叉树

2.为什么学习二叉树

前面学习的链表，如果我们需要检索出一个数据，有可能只需要检索一次，就可以找到数据，也有可能检索到最后一个节点才找到数据。这就是链表特性，寻找一条长度为N个节点的链表，搜索次数为1~N-1（头节点无效），二叉树的出现就是为了减少检索时的次数

3.什么是二叉树？

二义树是一种特殊的储存结构，是一种非线性的储存结构。所谓一棵树，都是有一个根节点，这个根节点也是可以用来存储数据的，二叉树结构就是把小于根节点的数据储存到根节点的左边，把大于根节点的数据储存到根节点的右边，这样就实现了检索数据时，例如，根节点是20，根左边是18，根右边是23，当我们需要守我一个数据为23时，就不需要去根节点的左边寻找只需要去根节点的右边寻找即可，所谓：义树搜索，就是不需要比较每一个节点，都可以快速找到日标，其效率要比链表高。

4.二叉树基本概念

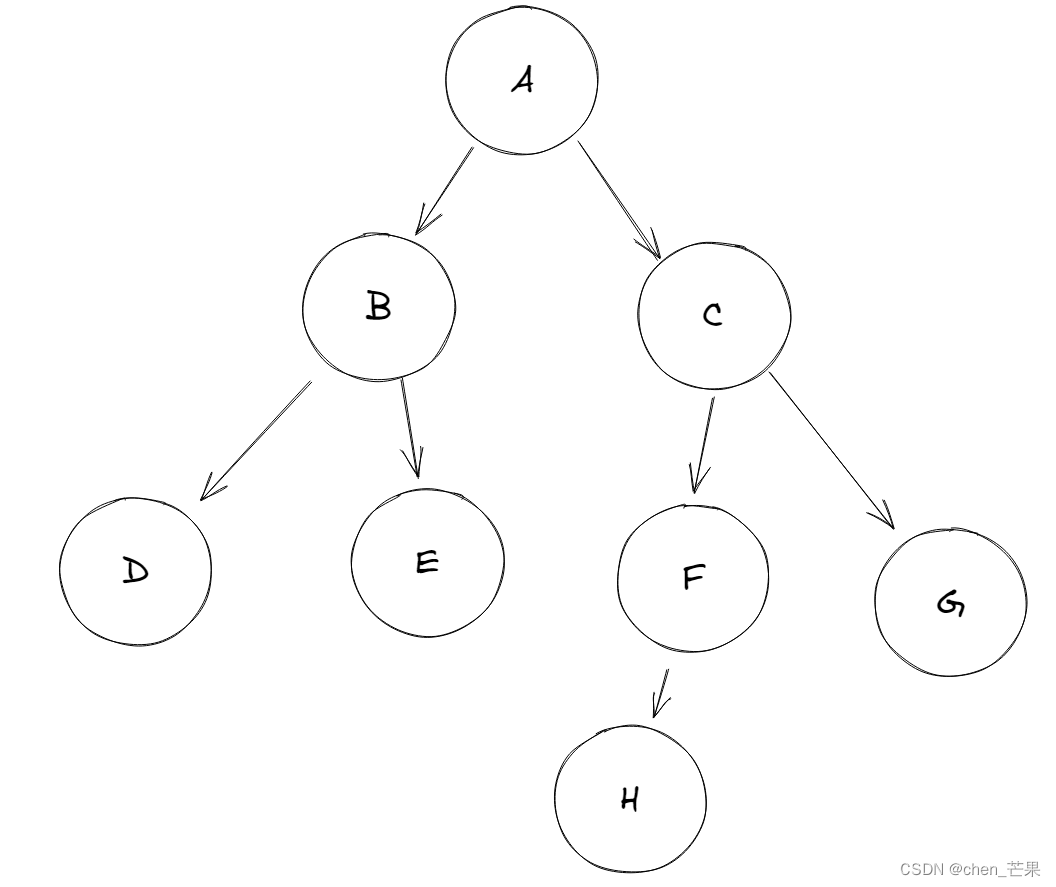
在这里插入图片描述

  1. 双亲和孩子：A是B/C的双亲，B/C是A的孩子
  2. 兄弟：拥有共同双亲的两个节点称为兄弟，B和C为兄弟 DE为兄弟
  3. 度：形容一个孩子的个数 A的度是2，C的度是2 ，F的度是1
  4. 层：A的层是1，B/C的层是2，DEFG的层是3

5.二叉树种类

  1. 只有一个根节点的二叉
    根是一棵树的基本，哪怕只有一个根节点，也可以形成二叉树
  2. 普通二叉树
    树上面任意的一个节点的度都是小于等于2的
  3. 满二叉树
    树上的任意一个节点的度都等于2。假设有一棵树，有N层，其树总结点个数达到2的N次方-1，每层度都为2，那么这棵树称为满二叉树
  4. 非二叉树
    只要树上有任意一个节点，其度大于2，那么这颗树就是非二叉树

6.左节点和右节点

一棵没有任何存储规则的二叉树是没有任何意义的，像上述所说的规则一样，把小于根节点的数据存储在左边，把大于根节点的数据放在右边，如果整棵树都遵循以上原则，就是有存储规律的树，那么左边的节点称为左节点，右边的节点称为右节点。

（二）二叉树模型

每一个节点都需要存储数据，所以都有数据域
每一个节点都需要有指向左节点的指针、每一个节点都需要有指向右节点的指针

//节点设计
struct node{
	int data;//数据域
    struct node* lchild;//指向左孩子指针
    struct node* rchild;//指向右孩子指针
};

3.二叉树增删改查

初始化根节点

struct node* init_new_node(struct node*root,int      num)
{
	//1.为新节点申请空间
	root = malloc(sizeof(struct node));
	if(root ==NULL)
		{
			printf("malloc new fail!\n");
	}

	//2.为新节点赋值
	root->data = num;
	root->lchild = NULL;
	root->rchild = NULL;

	return root;
}

插入数据

struct node* insert_node(struct node*new,struct node*root)
{
	//1.先判断树是否为空
	if(root==NULL)
	{
		return new;//如果这棵树没有根，那么这个新节点就作为根
	}
	//2.如果树不为空，则寻找正常位置插入数据
	if(new->data < root->data)//如果新节点比根节点小
	{
			root->lchild = insert_node(new,root->lchild);//那么让新节点与我的左孩子节点比较
	}
	else if(new->data > root->data)
	{
		root->rchild=insert_node(new,root->rchild);
	}
	else{
		printf("%d node already exists!\n",new->data);
	}
	
	return root;
}

在二叉树中搜索节点

struct node* find_node(struct node* root,int num)
{
	//1.如果这棵树没有根，那么这个新节点就作为根
		if(root==NULL)
		{
			return NULL;//返回空
		}
		if(num < root->data)//如果数字小于root，则去root的左节点
			{
			return find_node(root->lchild,num);
		}a
		else if(num > root->data)//如果数字大于root，则去root的右节点
			{
			return find_node(root->rchild,num);
		}
		else{
			return root;
		}

}

二叉树删除节点🔥

1. 如果需要删除的节点有左子树（不管有没有右子树），其方法是把左子树中最大值节点替换该节点
第一步：通过递归寻找需要删除的节点
第二步：找到这个删除节点的左子树的最大值
第三步：将这个最大值替换掉需要删除的节点
第四步：通过调用删除函数，递归删除最大值（不能直接删，需要递归删除，因为这个节点肯定没右子树，如果有右子树，这个节点肯定不是最大，但是可能存在左子树）。
例如要删除10节点时，找到10节点后，寻找10节点左子树的最大值，将找到 的最大值7替换10，然后递归删除最大值7，同理6替换7的位置
删除前二叉树：
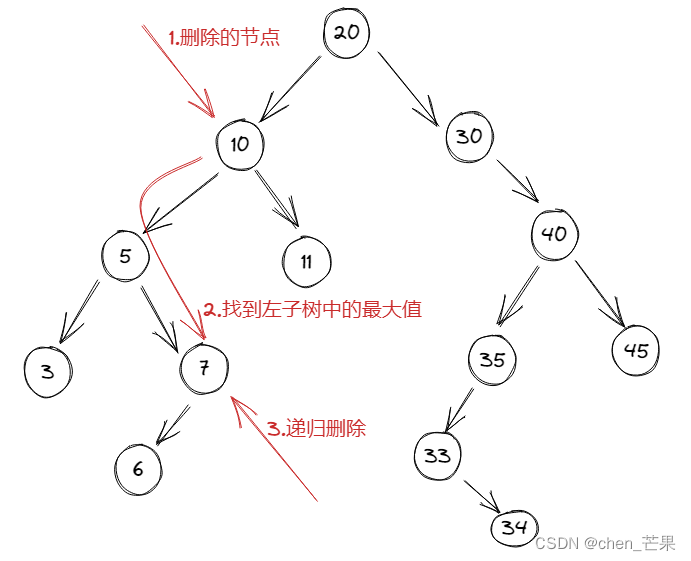
在这里插入图片描述
删除后二叉树：
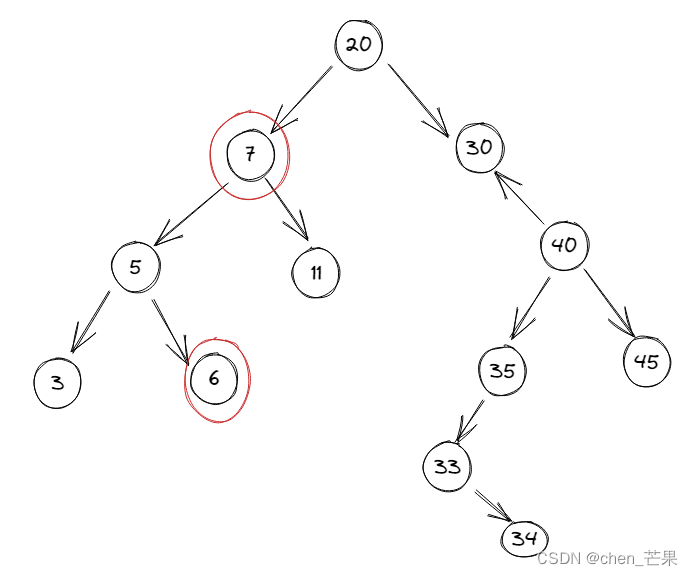
在这里插入图片描述
2. 如果需要删除的节点有右子树，，其方法是把右子树中最小值节点替换该节点
第一步：通过递归寻找需要删除的节点
第二步：找到这个删除节点的右子树的最小值
第三步：将这个最小值替换掉需要删除的节点
第四步：通过调用删除函数，递归删除最小值（不能直接删，需要递归删除，因为这个节点肯定没左子树，如果有左子树，这个节点肯定不是最小，但是可能存在右子树）。
例如要删除30节点时，找到30节点后，寻找30节点右子树的最小值，将找到 的最大值33替换30，然后递归删除最大值33，同理34替换33的位置
删除前二叉树：
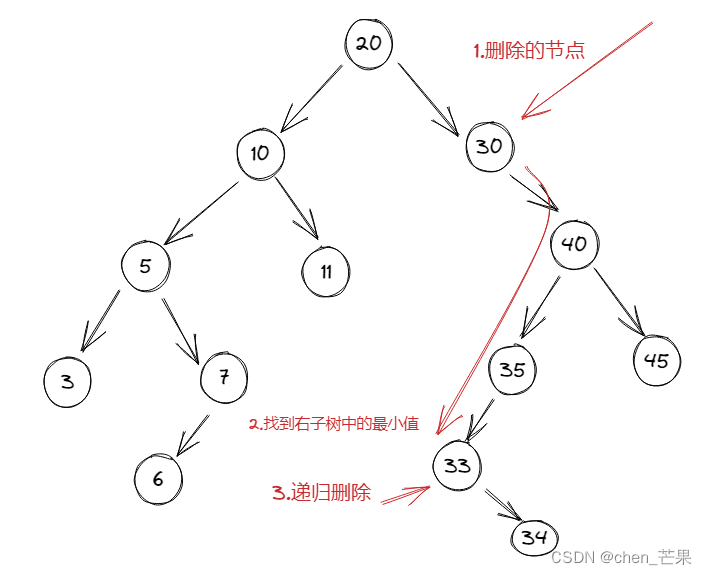
在这里插入图片描述
删除后二叉树：
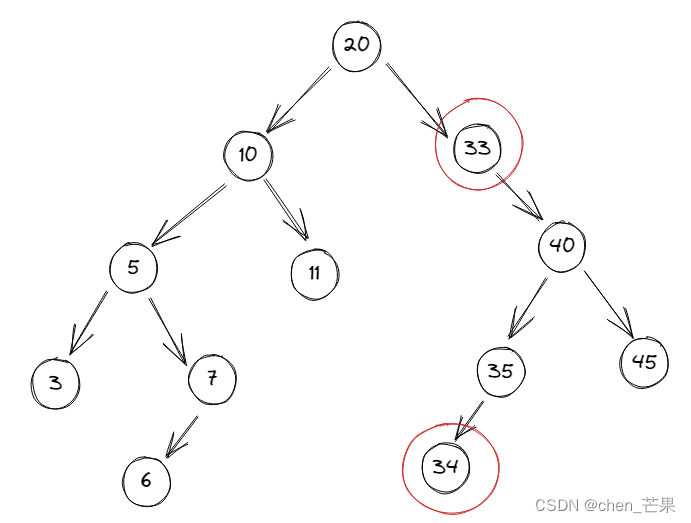
在这里插入图片描述

3. 如果需要删除的节点是一个度为0的节点，直接删除即可
第一步：通过递归寻找需要删除的节点
第二步：直接调用free()删除该节点的空间

struct node* delete_node(struct node* root,int num)
{
	//1.如果找到底都没有
	if(root == NULL)
	{
		return NULL;	
	}

	//2.寻找需要删除的节点
	if(num < root->data)
	{
		root->lchild = delete_node(root->lchild,num);
	}
	else if(num > root->data)
	{
		root->rchild = delete_node(root->rchild,num);
	}
	else {
		//3.判断需要删除的节点有没有左子树
		struct node* tmp=NULL;
		if(root->lchild!=NULL)//不为空则有左子树
		{
				//4.寻找左子树中的最大值
				for(tmp=root->lchild;tmp->rchild!=NULL;tmp = tmp->rchild);//循环找到最大值，结束循环tmp是最大值节点
				
				//5.将这个最大值替换root
				root->data = tmp->data;
				
				//6.递归删除tmp
				root->lchild = delete_node(root->lchild,tmp->data);
		}else if(root->rchild!=NULL)
				{
				//4.寻找右子树中的最小值
				for(tmp=root->rchild;tmp->lchild!=NULL;tmp = tmp->lchild);//循环找到最小值，结束循环tmp是最小值节点
				
				//5.将这个最小值替换root
				root->data = tmp->data;
				
				//6.递归删除tmp
				root->rchild = delete_node(root->rchild,tmp->data);
				}else
					{
						free(root);
						return NULL;
					}
		}
	return root;
}

遍历二叉树

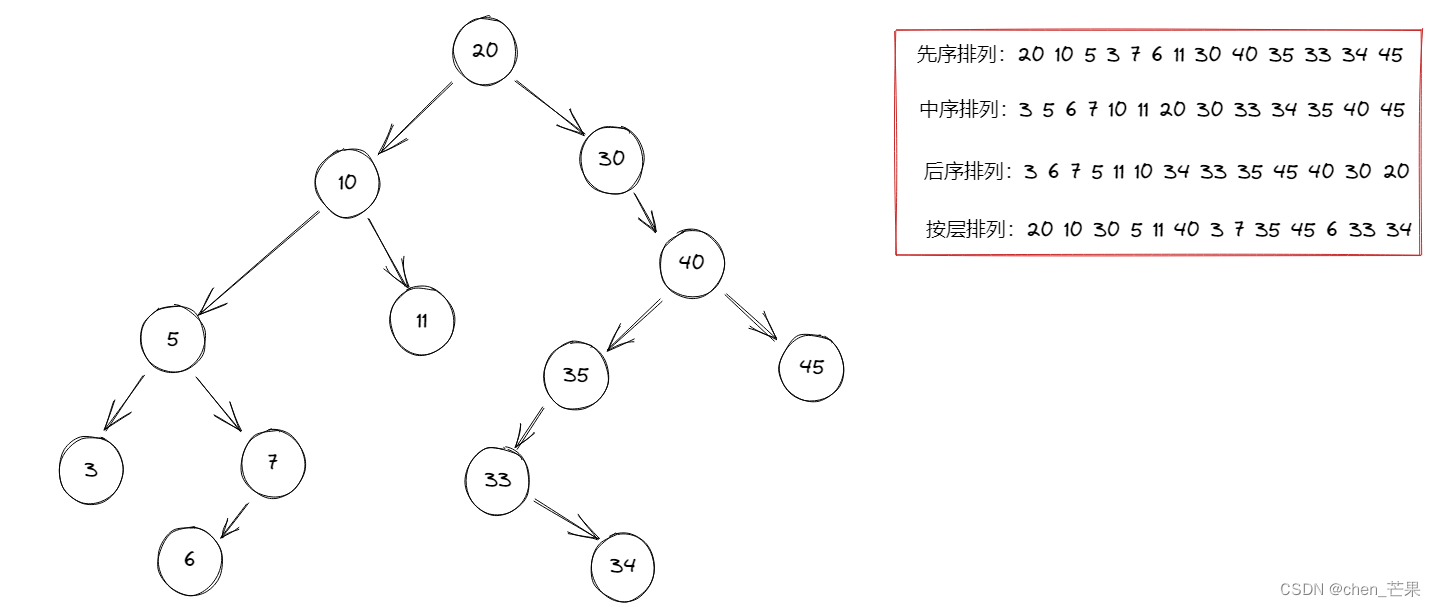
先序遍历

顺序：根->左->右

void show_node_first(struct node*root)
{
	if(root==NULL)
	{
		return;
	}
	printf("%d\n",root->data);	//根节点
	show_node_first(root->lchild);//左
	show_node_first(root->rchild);//右
}

中序遍历

顺序：左->根->右

void show_node_middle(struct node * root)
{
	if(root==NULL)
	{
		return;
	}
	show_node_middle(root->lchild);//左
	printf("%d\n",root->data);	//根节点
	show_node_middle(root->rchild);//右
}

后序遍历

顺序：左->右->根

void show_node_last(struct node *root)
{
	
	if(root==NULL)
	{
		return;
	}
	show_node_last(root->lchild);//左
	show_node_last(root->rchild);//右
	printf("%d\n",root->data);	//根节点
}

按层遍历

顺序：按每一层值遍历
设计步骤如下：
1.初始化一条空队
2.根节点入队
3.出队：如果出队失败，则结束程序；如果出队成功，则打印节点
4.打印刚刚出队的节点
5.判断刚刚出队的节点有没有左孩子，如果有则将左孩子入队
6.判断刚刚出队的节点有没有右孩子 ，如果有则右孩子入队
7.重复第三步


//设计一条队列的节点结构体
struct q_node{
	int data;
	struct q_node *next;
};

//设计队列的管理结构体
struct queue{
	struct q_node *head;
	struct q_node *tail;
	int size;
};


struct queue* init_queue(void)
{
	//为队列管理结构体申请空间
	struct queue* q = malloc(sizeof(struct queue));

	//为管理结构体赋值
	q->head =NULL;
	q->tail= NULL;
	q->size=0;

	return q;
}

int in_queue(struct queue*q,int num)
{
	//1.为新节点申请空间
	struct q_node* new=malloc(sizeof(struct q_node));
	if(new==NULL)
		{
			printf("malloc q_node error!\n");
	}

	//2.赋值
	new->data = num;
	new->next=NULL;

	if(q->size ==0)
		{
		q->head=new;
		q->tail=new;
	}else{
		q->tail->next = new;
		q->tail = new;
	}
	q->size++;
	return 0;
		
}

//出队
int out_queue(struct queue*q,int *a)
{
	if(q->size ==0)
	{
		return -1;	
	}

	struct q_node *tmp = q->head;

	if(q->size ==1){
		q->head =NULL;
		q->tail=NULL;
	}
	else{
		q->head = q->head->next;
	}

	*a = tmp->data;
	free(tmp);
	q->size--;

	return 0;
	
}

//按层遍历
int show_node_level(struct node*root)
{
	if(root ==NULL)
		{
		return -1;
	}

	//初始化一条空队
	struct queue* q = NULL;
	q=init_queue();

	//将根节点入队
	in_queue(q,root->data);

	//3.出队，
	int a;
	struct node*tmp=NULL;
	while(1)
	{
		//3.1	如果出队失败，则结束程序；
		if(out_queue(q,&a) == -1){
				break;
		}
		//3.2	如果出队成功，则打印节点 
		printf("%d\n",a);

		//4.在二叉树中找到刚刚出队的那个节点
		tmp = find_node(root,a);
		//5.判断刚刚出队的节点有没有左孩子，如果有则将左孩子入队
		if(tmp->lchild !=NULL)
		{
			in_queue(q,tmp->lchild->data);
		}
		if(tmp->rchild !=NULL){//判断刚刚出队的节点有没有右孩子 ，如果有则右孩子入队
			in_queue(q,tmp->rchild->data);
		}
	}
	free(q);
	return 0;	
}

在这里插入图片描述

（三）完整main函数

#include "stdio.h"
#include "stdlib.h"

struct node{
    int data;
    struct node * lchild;
    struct node * rchild;
};

//设计一条队列的节点结构体
struct q_node{
    int data;
    struct q_node *next;
};

//设计队列的管理结构体
struct queue{
    struct q_node *head;
    struct q_node *tail;
    int size;
};

struct node* init_new_node(struct node*root,int num)
{
    //1.为新节点申请空间
    root = malloc(sizeof(struct node));
    if(root ==NULL)
    {
        printf("malloc new fail!\n");
    }

    //2.为新节点赋值
    root->data = num;
    root->lchild = NULL;
    root->rchild = NULL;

    return root;
}

struct node* insert_node(struct node*new,struct node*root)
{
    //1.先判断树是否为空
    if(root==NULL)
    {
        return new;//如果这棵树没有根，那么这个新节点就作为根
    }
    //2.如果树不为空，则寻找正常位置插入数据
    if(new->data < root->data)//如果新节点比根节点小
    {
        root->lchild = insert_node(new,root->lchild);//那么让新节点与我的左孩子节点比较
    }
    else if(new->data > root->data)
    {
        root->rchild=insert_node(new,root->rchild);
    }
    else{
        printf("%d node already exists!\n",new->data);
    }

    return root;
}

struct node* find_node(struct node* root,int num)
{
    //1.如果这棵树没有根，那么这个新节点就作为根
    if(root==NULL)
        {
            return NULL;//返回空
        }
    if(num < root->data)//如果数字小于root，则去root的左节点
        {
            return find_node(root->lchild,num);
        }
    else if(num > root->data)//如果数字大于root，则去root的右节点
        {
            return find_node(root->rchild,num);
        }
    else{
            return root;
        }

}

struct node* delete_node(struct node* root,int num)
{
    //1.如果找到底都没有
    if(root == NULL)
    {
        return NULL;	
    }

    //2.寻找需要删除的节点
    if(num < root->data)
    {
        root->lchild = delete_node(root->lchild,num);
    }
    else if(num > root->data)
    {
        root->rchild = delete_node(root->rchild,num);
    }
    else {
        //3.判断需要删除的节点有没有左子树8
        struct node* tmp=NULL;
        if(root->lchild!=NULL)//不为空则有左子树
        {
            //4.寻找左子树中的最大值
            for(tmp=root->lchild;tmp->rchild!=NULL;tmp = tmp->rchild);//循环找到最大值，结束循环tmp是最大值节点

            //5.将这个最大值替换root
            root->data = tmp->data;

            //6.递归删除tmp
            root->lchild = delete_node(root->lchild,tmp->data);
        }else if(root->rchild!=NULL)
        {
            //4.寻找右子树中的最小值
            for(tmp=root->rchild;tmp->lchild!=NULL;tmp = tmp->lchild);//循环找到最小值，结束循环tmp是最小值节点

            //5.将这个最大值替换root
            root->data = tmp->data;

            //6.递归删除tmp
            root->rchild = delete_node(root->rchild,tmp->data);
        }else
        {
            free(root);
            return NULL;
        }
    }
    return root;
}


void show_node_first(struct node*root)
{
    if(root==NULL)
    {
        return;
    }

    printf("%d\n",root->data);	//根节点

    show_node_first(root->lchild);//左
    show_node_first(root->rchild);//右
}

void show_node_middle(struct node * root)
{
    if(root==NULL)
    {
        return;
    }

    show_node_middle(root->lchild);//左
    printf("%d\n",root->data);	//根节点
    show_node_middle(root->rchild);//右


}

void show_node_last(struct node *root)
{

    if(root==NULL)
    {
        return;
    }

    show_node_last(root->lchild);//左
    show_node_last(root->rchild);//右
    printf("%d\n",root->data);	//根节点
}

struct queue* init_queue(void)
{
    //为队列管理结构体申请空间
    struct queue* q = malloc(sizeof(struct queue));

    //为管理结构体赋值
    q->head =NULL;
    q->tail= NULL;
    q->size=0;

    return q;
}

int in_queue(struct queue*q,int num)
{
    //1.为新节点申请空间
    struct q_node* new=malloc(sizeof(struct q_node));
    if(new==NULL)
    {
        printf("malloc q_node error!\n");
    }

    //2.赋值
    new->data = num;
    new->next=NULL;

    if(q->size ==0)
    {
        q->head=new;
        q->tail=new;
    }else{
        q->tail->next = new;
        q->tail = new;
    }
    q->size++;
    return 0;

}

//出队
int out_queue(struct queue*q,int *a)
{
    if(q->size ==0)
    {
        return -1;	
    }

    struct q_node *tmp = q->head;

    if(q->size ==1){
        q->head =NULL;
        q->tail=NULL;
    }
    else{
        q->head = q->head->next;
    }

    *a = tmp->data;
    free(tmp);
    q->size--;

    return 0;

}

//按层遍历
int show_node_level(struct node*root)
{
    if(root ==NULL)
    {
        return -1;
    }

    //初始化一条空队
    struct queue* q = NULL;
    q=init_queue();

    //将根节点入队
    in_queue(q,root->data);

    //3.出队，
    int a;
    struct node*tmp=NULL;
    while(1)
    {
        //3.1	如果出队失败，则结束程序；
        if(out_queue(q,&a) == -1){
            break;
        }
        //3.2	如果出队成功，则打印节点 
        printf("%d\n",a);

        //4.在二叉树中找到刚刚出队的那个节点
        tmp = find_node(root,a);
        //5.判断刚刚出队的节点有没有左孩子，如果有则将左孩子入队
        if(tmp->lchild !=NULL)
        {
            in_queue(q,tmp->lchild->data);
        }
        if(tmp->rchild !=NULL){//判断刚刚出队的节点有没有右孩子 ，如果有则右孩子入队
            in_queue(q,tmp->rchild->data);
        }
    }
    free(q);
    return 0;	
}



int main(int argc,char *argv[])
{
    //1.初始化根节点
    struct node*root =NULL;
    root = init_new_node(root,20);

    //2.插入节点到二叉树中
    struct node*new1=NULL;
    new1 = init_new_node(new1,10);
    insert_node(new1,root);

    struct node*new2=NULL;
    new2 = init_new_node(new2,30);
    insert_node(new2,root);

    struct node*new3=NULL;
    new3 = init_new_node(new3,5);
    insert_node(new3,root);	

    struct node*new4=NULL;
    new4 = init_new_node(new4,11);
    insert_node(new4,root);

    struct node*new5=NULL;
    new5 = init_new_node(new5,40);
    insert_node(new5,root);

    struct node*new6=NULL;
    new6 = init_new_node(new6,3);
    insert_node(new6,root);

    struct node*new7=NULL;
    new7 = init_new_node(new7,7);
    insert_node(new7,root);

    struct node*new8=NULL;
    new8 = init_new_node(new8,35);
    insert_node(new8,root);

    struct node*new9=NULL;
    new9 = init_new_node(new9,45);
    insert_node(new9,root);

    struct node*new10=NULL;
    new10 = init_new_node(new10,6);
    insert_node(new10,root);

    struct node*new11=NULL;
    new11 = init_new_node(new11,33);
    insert_node(new11,root);

    struct node*new12=NULL;
    new12 = init_new_node(new12,34);
    insert_node(new12,root);


    //3.在二叉树中搜索节点
    struct node* tmp = find_node(root,33);
    if(tmp!=NULL)
    {
        printf("二叉树寻找的目标:%d\n",tmp->data);
    }
    else
    {
        printf("二叉树中没有这个节点\n");
    }
    printf("==============\n");

    //4.删除二叉树节点
    /*
printf("delete before root->lchild->data:%d\n",root->lchild->data);
/delete_node(root,10);
printf("delete after root->lchild->data:%d\n",root->lchild->data);
printf("delete beforeroot->rchild->data:%d\n",root->rchild->data);
delete_node(root,30);
printf("delete after root->rchild->data:%d\n",root->rchild->data);
printf("==============\n");
*/
    //5.先序遍历：根->左->右
    show_node_first(root);
    printf("==============\n");

    //6.中序遍历
    show_node_middle(root);
    printf("==============\n");

    //7.后序遍历
    show_node_last(root);
    printf("==============\n");

    //8.按层遍历
    show_node_level(root);
    printf("==============\n");
    return 0;

}
  数据结构与算法 最新文章
【力扣106】 从中序与后续遍历序列构造二叉
leetcode 322 零钱兑换
哈希的应用：海量数据处理
动态规划|最短Hamilton路径
华为机试_HJ41 称砝码【中等】【menset】【
【C与数据结构】——寒假提高每日练习Day1
基础算法——堆排序
2023王道数据结构线性表--单链表课后习题部
LeetCode 之 反转链表的一部分
【题解】lintcode必刷50题＜有效的括号序列
上一篇文章      下一篇文章      查看所有文章
加:2022-09-13 11:43:26  更:2022-09-13 11:46:57 
 
开发: C++知识库 Java知识库 JavaScript Python PHP知识库 人工智能 区块链 大数据 移动开发 嵌入式 开发工具 数据结构与算法 开发测试 游戏开发 网络协议 系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑 笔记本 显卡 显示器 固态硬盘 硬盘 耳机 手机 iphone vivo oppo 小米 华为 单反 装机 图拉丁

360图书馆 购物 三丰科技 阅读网 日历 万年历 2024年5日历 -2024/5/19 12:11:33-

图片自动播放器
↓图片自动播放器↓ 		TxT小说阅读器
↓语音阅读,小说下载,古典文学↓ 		一键清除垃圾
↓轻轻一点,清除系统垃圾↓ 		图片批量下载器
↓批量下载图片,美女图库↓
  网站联系: qq:121756557 email:121756557@qq.com  IT数码