一:移动零(力扣283)
void moveZeroes(vector<int>& nums) { //申请一个辅助数组,存放非零元素,然后再赋值给原数组 vector<int> aux; for(int i=0;i<nums.size();i++){ if(nums[i]) aux.push_back(nums[i]);//借用向量的push_back函数 } for(int i=0;i<aux.size();i++){ nums[i]=aux[i]; } //补0 for(int i=aux.size();i<nums.size();i++){ nums[i]=0; } }很简单的一个思路:
? ? ? ?申请额外数组存储原数组非零元素(利用push_back),然后赋值回给原数组,最后在末位编变成0
法二:
void moveZeroes(vector<int>& nums) { /* 原地实现该功能,不申请额外空间: 定义一个索引k,指向数组第一个元素,i用于遍历数组,如果是非零元素把值赋给k位置。 k更新到下一个位置,直至遍历结束,从k开始往后补0 */ int k=0;//nums中[0,k)存储非零元素 //for循环,不断把非零元素依次赋值给k for(int i=0;i<nums.size();i++) if(nums[i]){//nums[i]不为0 nums[k++]=nums[i];//别忘了移动k索引 } //补零 for(int i=k;i<nums.size();i++) nums[i]=0; }法三:零与非零的交换
void moveZeroes(vector<int>& nums) { int k=0;//nums中[0,k)存储非零元素 for(int i=0;i<nums.size();i++) if(nums[i]){ swap(nums[i],nums[k]); k++; } }与法二相比,由于直接交换,少了重新赋值为0操作
优化细节:
避免自己和自己交换,可以考虑i与k的大小关系
if(i!=k)? swap(nums[k++],nums[i]);
else k++;
二:挑选颜色
void sortColors(vector<int>& nums) { /* 因为元素只有0,1,2三种可能,所以采用计数排序思想: 分别统计出:0的个数,1的个数以及2的个数,赋值即可 */ int count[3]={0}; for(int i=0;i<nums.size();i++){ assert(nums[i]>=0&&nums[i]<=2); count[nums[i]]++;//数值直接对应频次 } //定义一个不断累计的索引 int index=0; for(int i=0;i<count[0];i++) nums[index++]=0; for(int i=0;i<count[1];i++) nums[index++]=1; for(int i=0;i<count[2];i++) nums[index++]=2; }几个代码小细节:
- 因为只有0,1,2且想累计出现个数,直接以元素值计算频次
- 由于从头一次按照个数赋值0,1,2;所以直接建立一个不断累计的index
?其实可以把三路快排的思想移到这
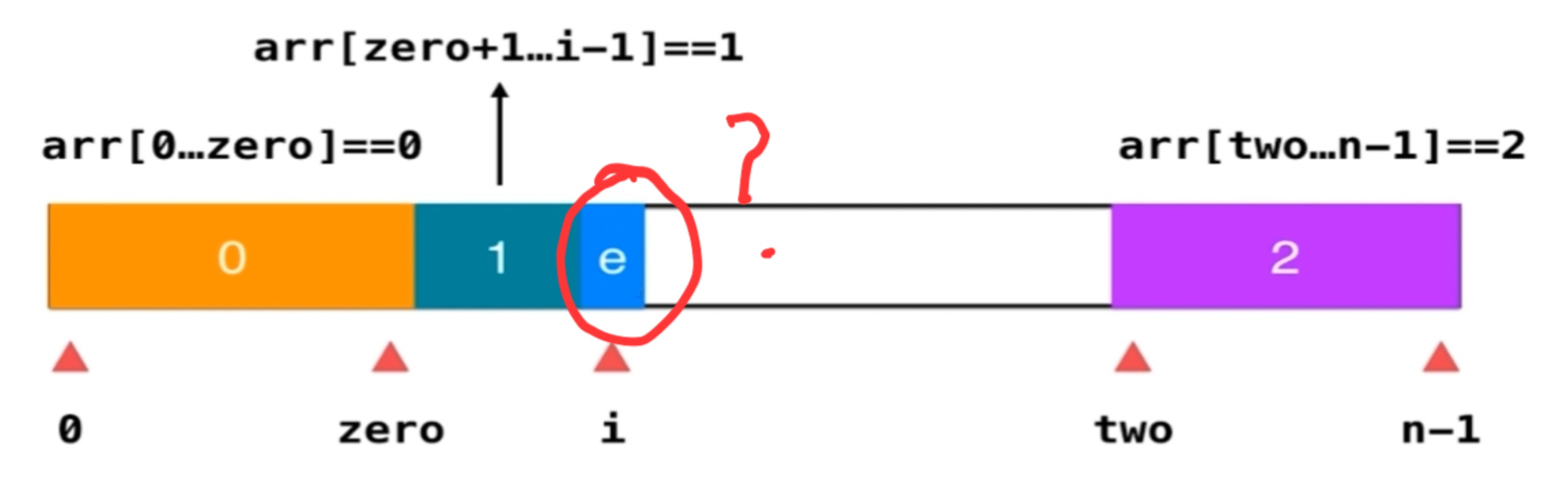
这是最后想达到的效果:
?其实关键在于对遍历索引i的元素处理:
?分以下三种情况:
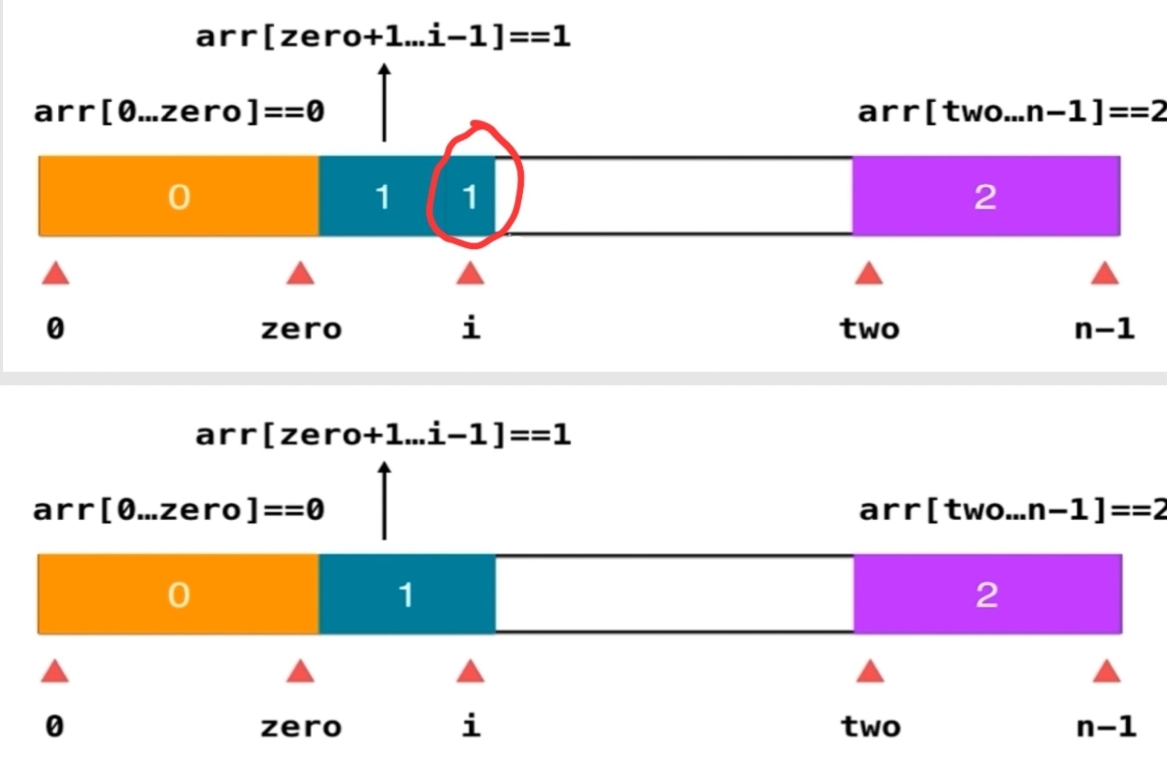
?如果元素为1,i右移
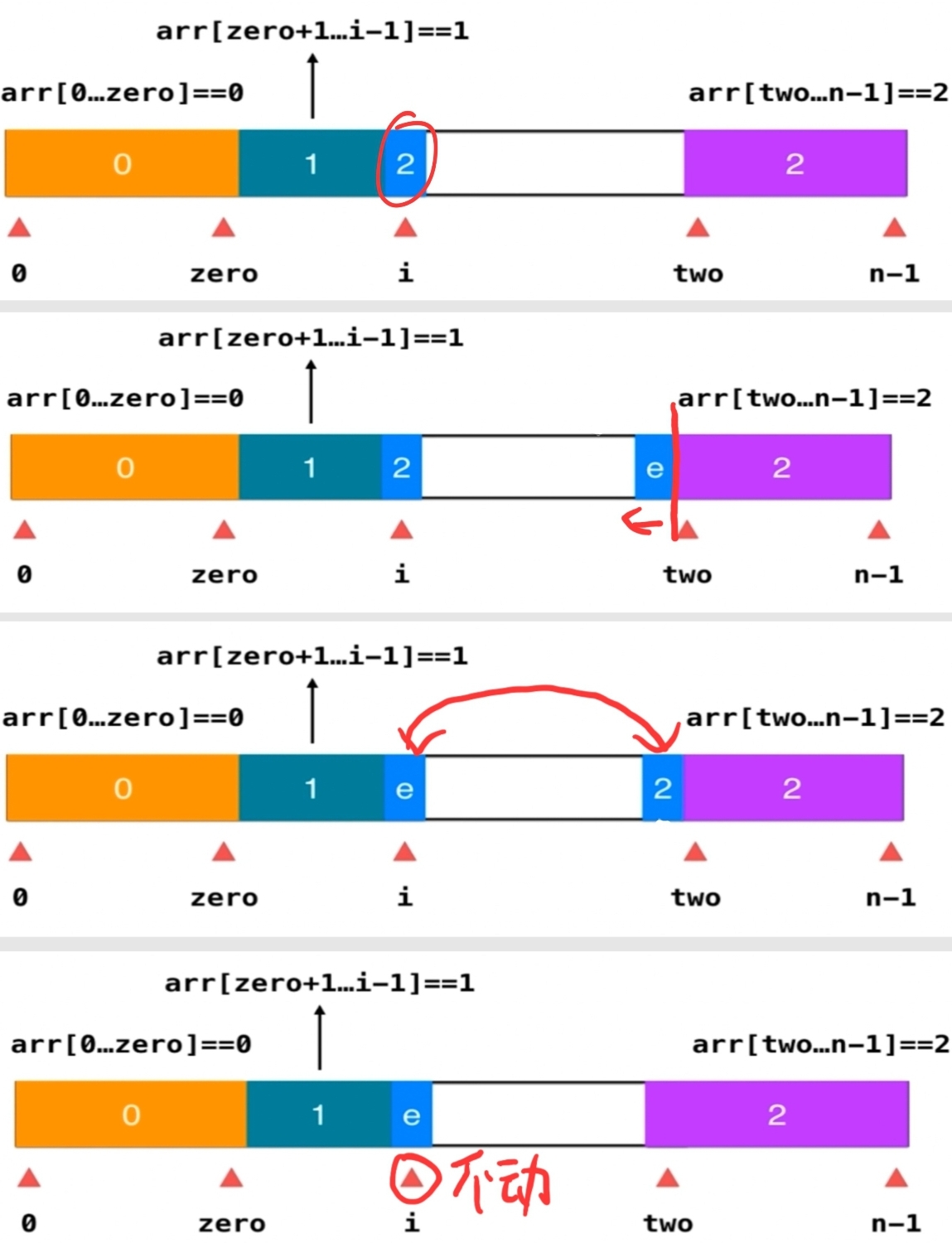
?如果元素是2,和two前一个元素交换,i不动,two--
?如果元素是1,和zero后元素交换,zero++,i++
代码实现
#include<iostream> #include<vector> using namespace std; class soluction{ public: void sortColors(vector<int>& nums){ /* 功能实现: [0,zero]全是0----也就是zero初始化为-1 [two,n-1]全是1---也就是two初始化为n(假设nums长度为n) 索引i遍历数组,遇到1右移,控制(zero,two)范围全是1 */ int zero=-1; int two=nums.size(); int i=0;//从头遍历数组 while( i<two ){//遍历结束条件 if(nums[i]==1) i++; else if(nums[i]==2){ two--; swap(nums[two],nums[i]); } else{//nums[i]==0 zero++; swap(nums[i],nums[zero]); i++; } } } }; int main(){ int arr[]={1,0,2,0,2,1,1,2,0}; vector<int> vec(arr,arr+sizeof(arr)/sizeof(int)); soluction().sortColors(vec); for(vector<int>::iterator it=vec.begin();it!=vec.end();it++) cout<<(*it)<<" "; }
快速排序两种实现
#include<iostream> #include<vector> using namespace std; int partition(vector<int>& a,int L,int R){ /* 索引i记录小于基准元素的最后一个位置,初始化为基准元素位置 索引j用于遍历 j遇到的元素≥基准元素---往后遍历 j遇到的元素<基准元素---交换i后位置和当前位置,i++ */ int e=a[L];//以最左边元素为基准元素 int i=L; int j=L+1; for(;j<=R;j++){ if(a[j]<e){ swap(a[++i],a[j]); } } swap(a[L],a[i]); return i; } void quickSortHelper(vector<int>& a,int L,int R){ if(L>=R) return;//递归结束 int p=partition(a,L,R); quickSortHelper(a,L,p-1); quickSortHelper(a,p+1,R); } void quickSort(vector<int>& a){//一定要加& quickSortHelper(a,0,a.size()-1); } int main(){ vector<int> arr={1,22,3,55,66,7,2,11,1,3,4}; quickSort(arr); vector<int>::iterator it; for(it=arr.begin();it!=arr.end();it++){ cout<<(*it)<<" "; } return 0; }注意要在vector加上*,否则原向量不改变
/* 双指针法: i不断右移,使得其之前的元素均≤基准元素 j不断左移,使得其之后的元素均≥基准元素 如果i,j均停止,交换两者所指元素,然后i右移,j左移 最后----把j位置,即小于基准元素最后一个元素和基准元素交换 */ int e=a[L]; int i=L+1,j=R;//i,j指向除基准元素的两头 while(1){ while(i<=j&&a[i]<=e) i++; while(i<=j&&a[j]>=e) j--; if(i>j) break; swap(a[i++],a[j--]); } swap(a[L],a[j]); return j; }
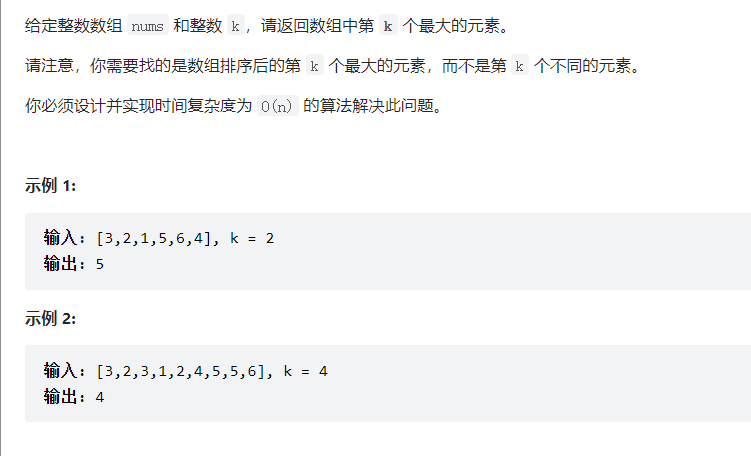
?三:寻找第k个大的元素
?这里要用到一个快速排序分区的性质:
每次快排后,都可以确定该元素在顺序中的正确位置。
也就是说:排序后,倒数第一个最大,倒数第二个第二大。。。。
只要快排的索引落在了该位置,该位置就可以确定第几大或第几小
int partition(vector<int>& nums,int l,int r){ int e=nums[l]; int i=l; int j=l+1; for(;j<=r;j++){ if(nums[j]<e) swap(nums[j],nums[++i]); } swap(nums[l],nums[i]); return i; } int findKthLargest(vector<int>& nums, int k) { int target=nums.size()-k; int l=0; int r=nums.size()-1; while(1){//条件:L<=R,但是该题一定有解,无需判断 int p=partition(nums,l,r); if(p==target) return nums[p]; else if(p>target) r=p-1; else l=p+1; } }