[数据结构与算法][LeetCode周赛复盘] 第 310 场周赛20220911

一、本周周赛总结

• 排名还在掉，先截图吧。
• T2不仔细wa了一发，很难受。
• T4从来没想过LIS还能用线段树优化，后来想想确实是没错，反正大概是上网找了个类似题抄了思路赶紧写的线段树。
• T3又是堆，最近堆出现的好多。
  

二、 [Easy] 6176. 出现最频繁的偶数元素

链接: 6176. 出现最频繁的偶数元素

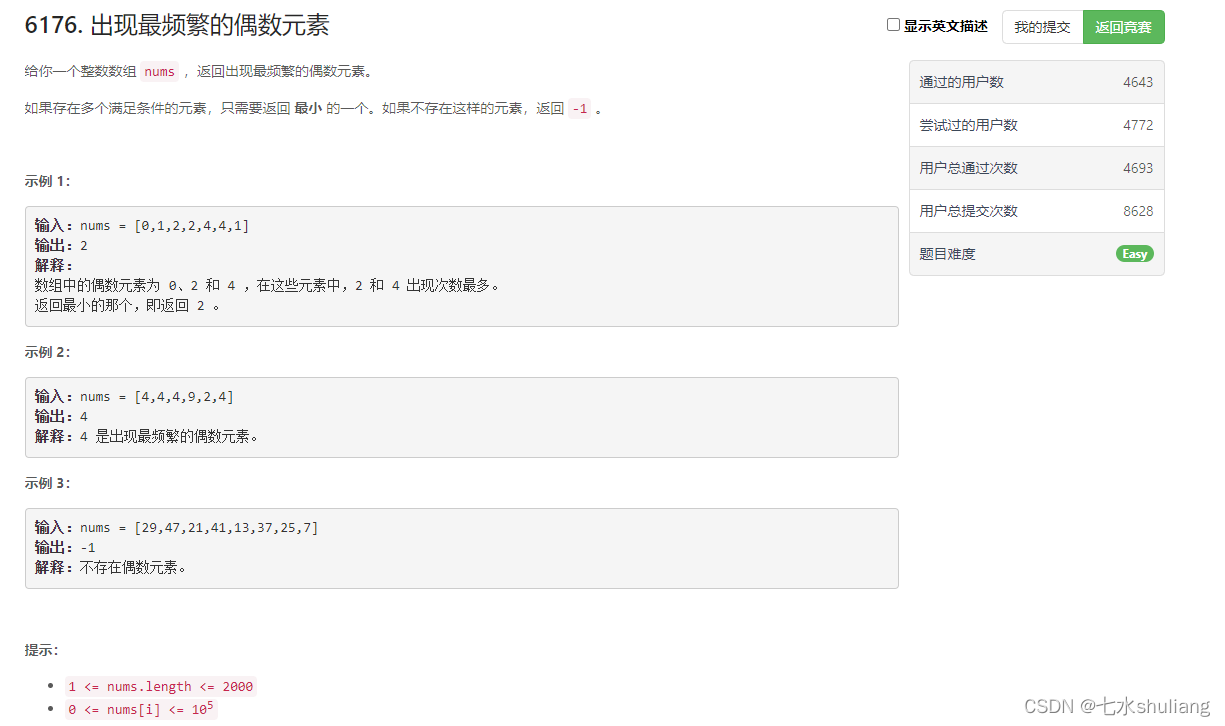
1. 题目描述

2. 思路分析

• 直接计数偶数，然后遍历即可。
• 要注意如果没有偶数ans应该是-1，但是ans又要取小的，因此先定义成10**6最后发现没变就改成-1.

3. 代码实现

class Solution:
    def mostFrequentEven(self, nums: List[int]) -> int:
        cnt = Counter(n for n in nums if (n&1) == 0)
        ans = 10**6
        for k,v in cnt.items():
            if v > cnt[ans]:
                ans = k
            elif v == cnt[ans]:
                ans = min(ans,k)
        if ans == 10**6:
            ans = -1
        return ans

三、[Medium] 6177. 子字符串的最优划分

链接: 6177. 子字符串的最优划分

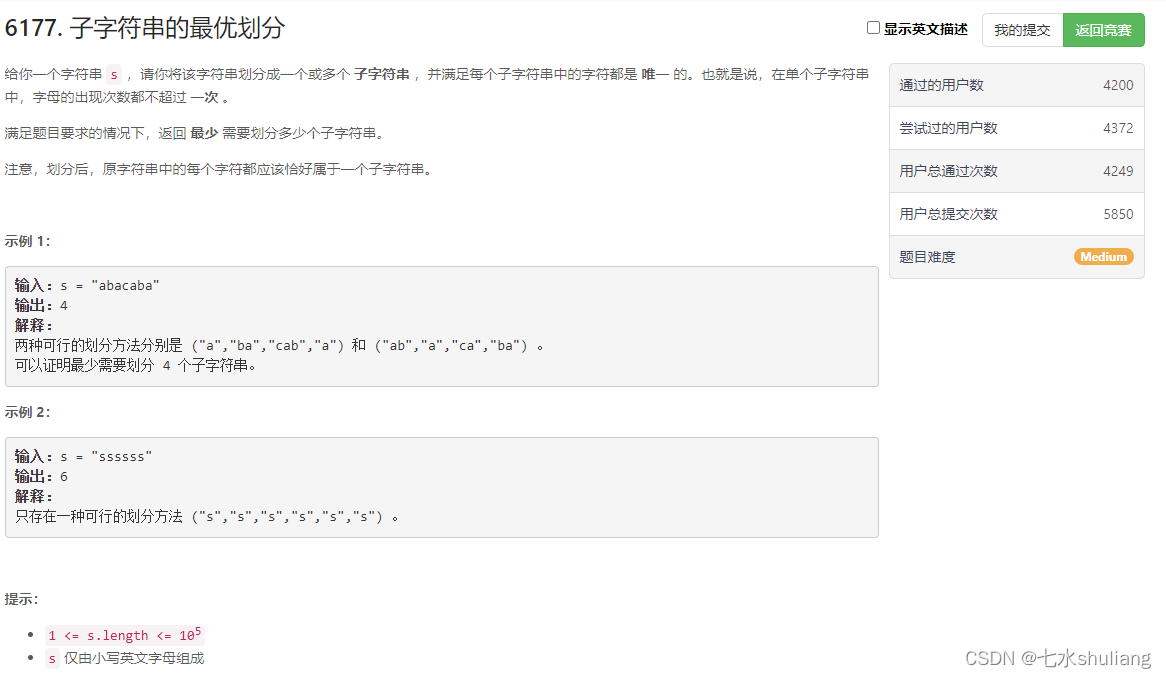
1. 题目描述

2. 思路分析

定级Medium。

• 定义一个计数器，记录每一段中字符出现次数，当发现字符出现2次时，重新起段。
• 最后数一共多少段即可。
• 这里wa了一次，因为不起段时忘记计数了。
• 由于这里最多一次，其实用set更快。

3. 代码实现

class Solution:
    def partitionString(self, s: str) -> int:
        n = len(s)
        ans = 1
        cnt = Counter()
        cnt[s[0]] = 1
        for r in range(1,n):
            # print(s[r],cnt)
            if s[r] in cnt:
                ans += 1
                cnt = Counter(s[r:r+1])
            else:
                cnt[s[r]] += 1
        return ans    

四、[Medium] 6178. 将区间分为最少组数

链接: 6178. 将区间分为最少组数

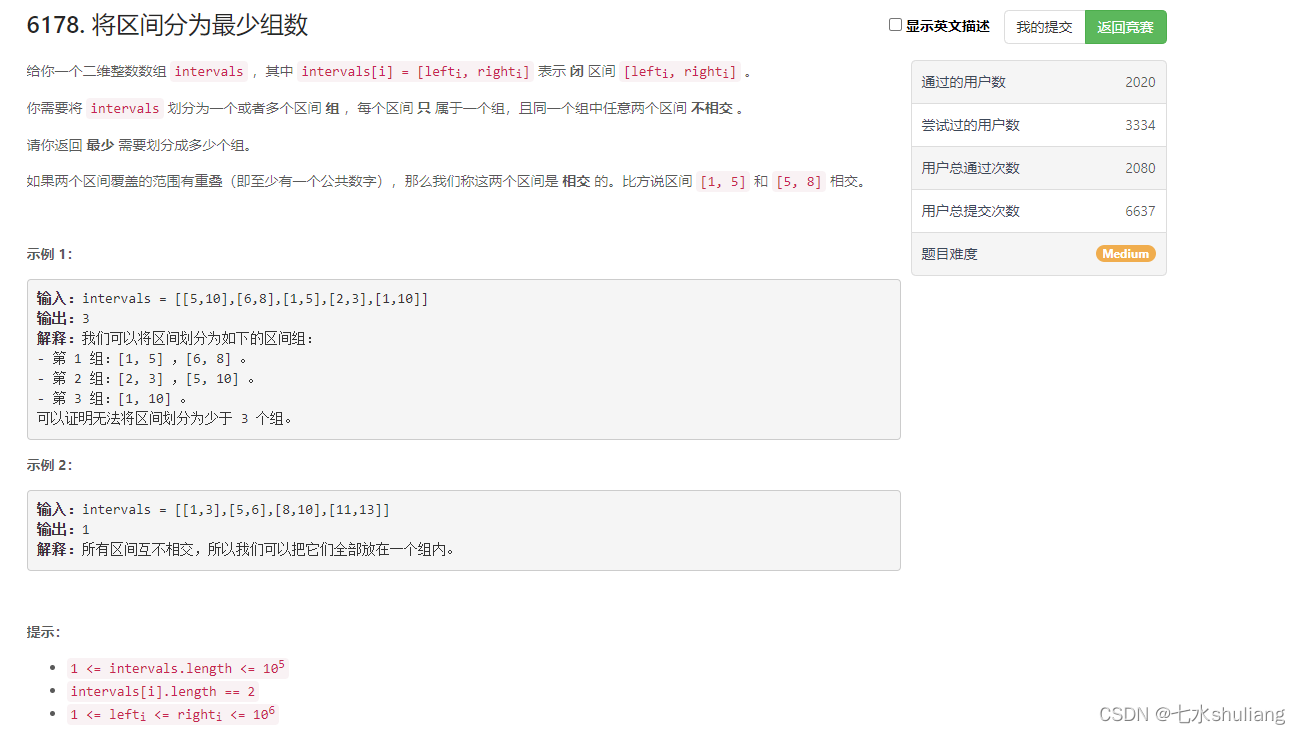
1. 题目描述

2. 思路分析

定级Medium。

• 又是堆。
• 相当于安排会议室，[l,r]是会议开始结束时间，有空闲就安排一个空闲的；如果没有空闲会议室就盖一个新的会议室（/doge）。
• 把会议按开始时间排序，因为先开始的要优先安排会议室。
• 用小顶堆来维护每个会议室最后一个会议的结束时间（也就是能空闲出来的时间）。
• 如果堆顶（最早空出来的时间）的会议室能满足当前会议，则安排，把这个会议室时间更新成当前会议的结束时间。
• 否则新盖一个会议室（push）。

3. 代码实现

class Solution:
    def minGroups(self, intervals: List[List[int]]) -> int:
        n = len(intervals)
        intervals.sort(key=lambda x :x[0])
        
        h = []
        
        for l,r in intervals:
            if h and h[0]<l:
                heapq.heapreplace(h,r)
            else:
                heapq.heappush(h,r)
        return len(h)

五、[Hard] 6206. 最长递增子序列 II

链接: 6206. 最长递增子序列 II

1. 题目描述

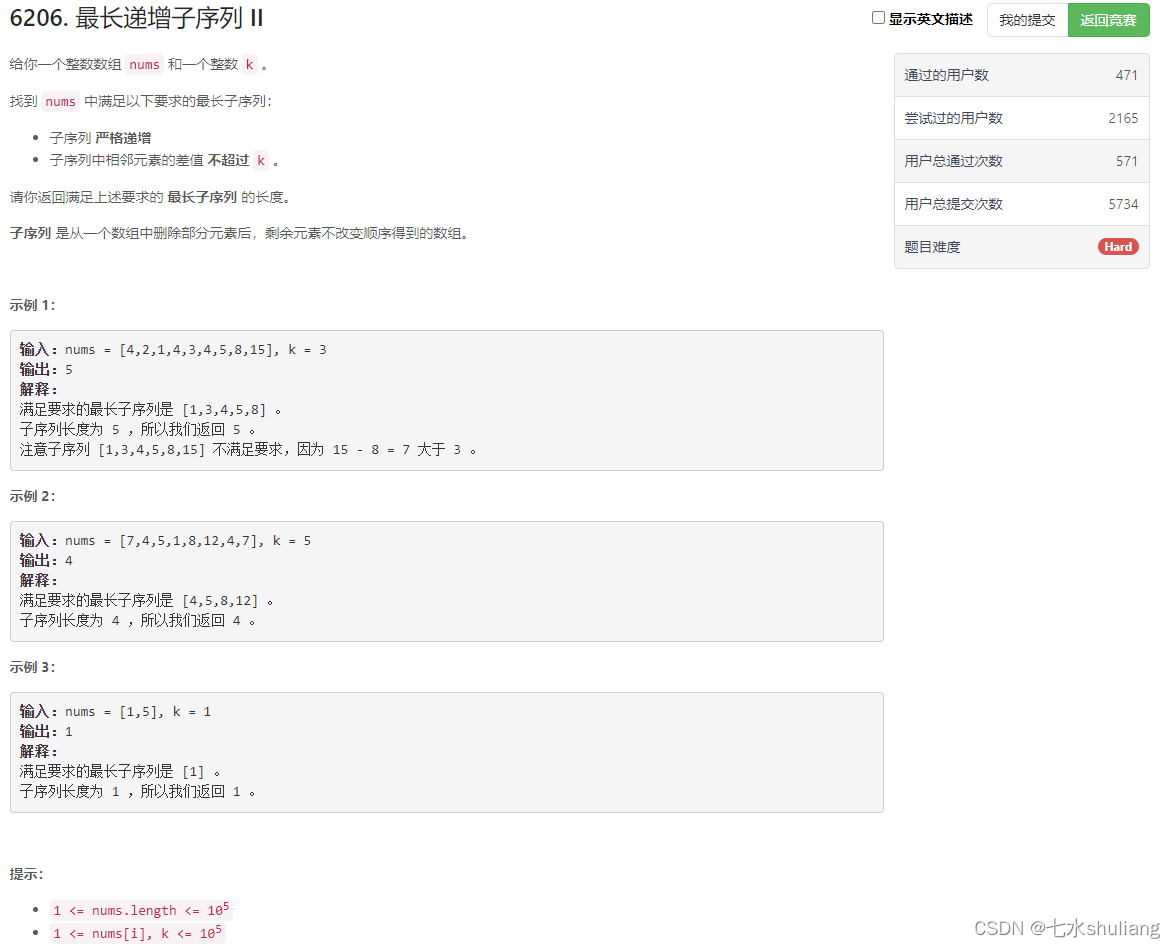
2. 思路分析

定级Hard。

• 看了眼数据结构，朴素dp的N方做法肯定过不了。
• 试了下单调二分优化的nlgn做法，wa了。
• 最后还是回到朴素DP的优化，先看朴素解法：
• 令f[i]为以第i个数位结尾的LIS长度（这里LIS指带限制的LIS，即相差不超过K，下边不再赘述）。
• 显然f[i] = max{f[j]|j<i 且a[j]<a[i] 且a[i]-a[j]<=k}+1。
• 这样的做法是O(n^2)的。
• 我们发现，j的限制条件其实是指i前边比a[i]所有小的数，且这个数的范围是[a[i]-k,a[i]-1]。
• 那么我们可以用线段树来维护这个区间所有数字f的最大值。
• 这样每次操作的时间复杂度优化到了lgn，总体复杂度O(nlgn)就可以过了。

3. 代码实现

class IntervalTree:
    def __init__(self, size,nums=None):
        self.size = size
        self.nums = nums
        self.interval_tree = [0]*(size*4)

    def update_point(self,p,l,r,index,val):        
        if index < l or r < index:
            return 
        interval_tree = self.interval_tree
        interval_tree[p] =max(interval_tree[p],val)
        if l == r:
            return
        mid = (l+r)//2
        if index <= mid:
            self.update_point(p*2,l,mid,index,val)
        else:
            self.update_point(p*2+1,mid+1,r,index,val)
    
    def query(self,p,l,r,x,y):
        """
        查找x,y区间的最大值        """        
        
        if y < l or r < x:
            return 0
        if x<=l and r<=y:
            return self.interval_tree[p]
        
        mid = (l+r)//2
        s = 0
        if x <= mid:
            s = max(s,self.query(p*2,l,mid,x,y))
        if mid < y:
            s = max(s,self.query(p*2+1,mid+1,r,x,y))
        return s

    
class Solution:
    def lengthOfLIS(self, nums: List[int], k: int) -> int:
        n = len(nums)
        mx = max(nums)
        tree = IntervalTree(mx)
        ans = 0
        for i in range(n):
            v = nums[i]
            l = max(0,v-k)
            r = max(0,v-1)
            ret = tree.query(1,1,mx,l,r)+1
            tree.update_point(1,1,mx,v,ret)
            ans = max(ans,ret)

        return ans

六、参考链接

• 链接: [python刷题模板] 线段树