文章目录
1 排序概述
将杂乱无章的数据元素,通过一定的方法按关键字顺序排列的过程叫做排序。
排序的分类:
(1)内部排序:指将需要处理的所有数据都加载到内部存储器中进行排序。
(2)外部排序:数据量过大,无法全部加载到内存中,需要借助外部存储进行排序。
常见的排序算法分类如下图所示,本文主要讨论内部排序。

2 插入排序
2.1 直接插入排序
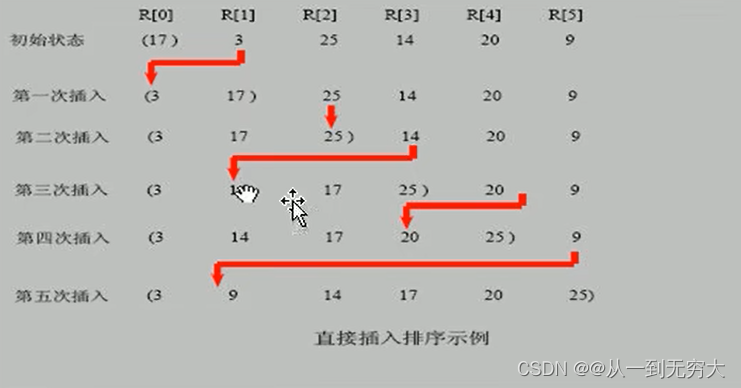
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
插入排序的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
public static void directInsertSort(int[] arr){
for (int i = 1; i < arr.length; ++i){
for (int j = i; j > 0; --j){
if (arr[j] < arr[j - 1]){
swap(arr, j, j - 1);
} else {
break;
}
}
}
}
public static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
2.2 希尔排序
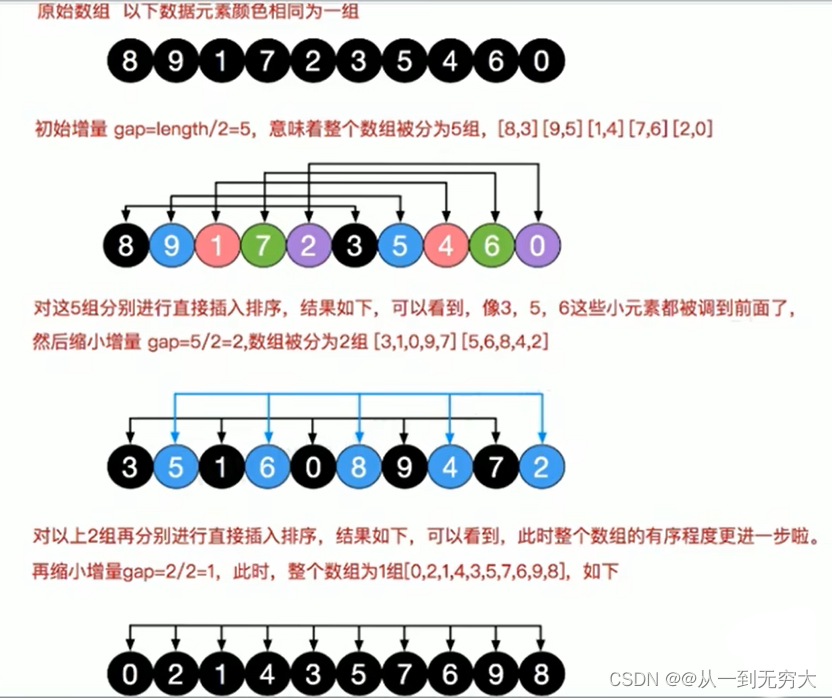
希尔排序法基本思想:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
public static void shellSort(int[] arr){
int gap = arr.length;
while (true){
gap /= 2;
for (int i = 0; i < gap; ++i){
for (int j = i + gap; j < arr.length; j += gap){ // 这个循环里其实就是一个插入排序
int k = j;
while (k >= gap && arr[k] < arr[k - gap]){
swap(arr, k, k - gap);
k -= gap;
}
}
}
if (gap == 1){
break;
}
}
}
3 选择排序
3.1 简单选择排序
简单选择排序思想:第1次从arr[0]~arr[n-1]中选取最小值,与arr[0]交换,第二次从arr[1] ~arr[n-1]中选取最小值,与arr[1]交换,第三次从arr[2] ~arr[n-1]中选取最小值,与arr[2]交换,…,第n-1次从arr[n-2] ~arr[n-1]中选取最小值,与arr[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
public static void simpleSelectSort(int[] arr){
int n = arr.length;
for (int i = 0; i < n - 1; ++i){
int minIndex = i;
for (int j = i + 1; j < n; ++j){
if (arr[j] < arr[minIndex]){
minIndex = j;
}
}
if (i != minIndex){
swap(arr, i, minIndex);
}
}
}
3.2 堆排序
堆排序基本介绍
(1)堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序。
(2)堆是具有以下性质的二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆。
(3)每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
(4)大顶堆如下图所示:
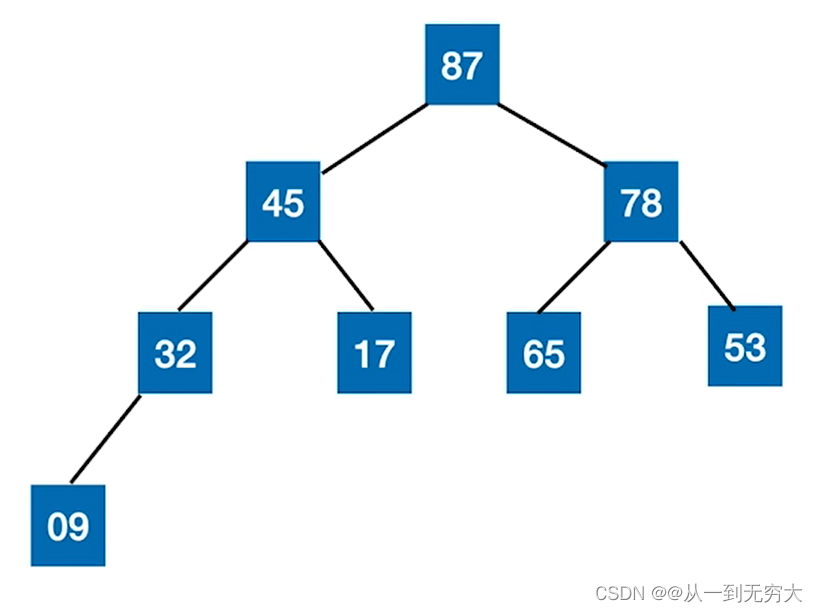
堆排序基本思想
(1)将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点;
(2)将其与末尾元素进行交换,此时末尾就为最大值;
(3)然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值,如此反复执行,便能得到一个有序序列了。
public static void heapSort(int[] arr){
// 将数组调整为大根堆
for (int i = arr.length / 2 - 1; i >= 0; --i){ // 因为数组从0开始计数,所以要减1
adjustHeap(arr, i, arr.length);
}
// 排序
for (int i = arr.length - 1; i > 0; --i){
swap(arr, 0, i);
adjustHeap(arr, 0, i);
}
}
public static void adjustHeap(int[] arr, int i, int length){
for (int k = 2 * i + 1; k < length; k = 2 * k + 1){ // 因为数组从0开始计数,所以要加1
if (k + 1 < length && arr[k] < arr[k + 1]){ // 选取左,右孩子当中较大的值与父节点交换
++k;
}
if (arr[i] < arr[k]){
swap(arr, i, k);
i = k; // 继续调整子树当中的节点
} else {
break;
}
}
}
4 交换排序
4.1 冒泡排序
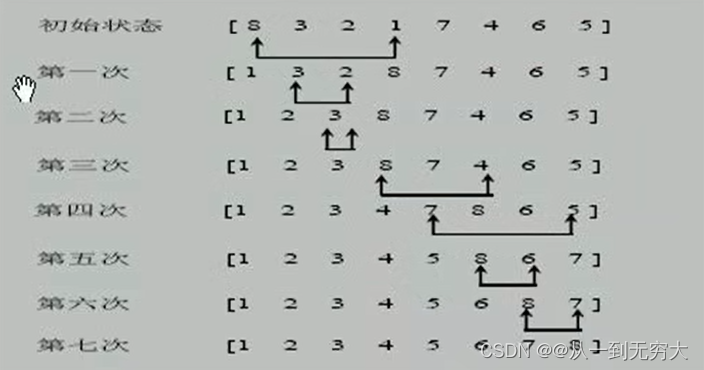
冒泡排序基本思想:通过对待排序序列从前向后(从下标较小的元素开始),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就像水底下的气泡一样逐渐向上冒。
因为排序的过程中各元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志flag判断元素是否进行过交换,从而减少不必要的比较。
public static void bubbleSort(int[] arr){
for (int i = 0; i < arr.length - 1; ++i){
boolean flag = true; // 标识变量,表示是否进行过交换
for (int j = 0; j < arr.length - i - 1; ++j){
if (arr[j] > arr[j + 1]){
flag = false;
swap(arr, j, j + 1);
}
}
if (flag){
break;
}
}
}
4.2 快速排序
快速排序法基本思想:快速排序是对冒泡排序的一种改进,基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
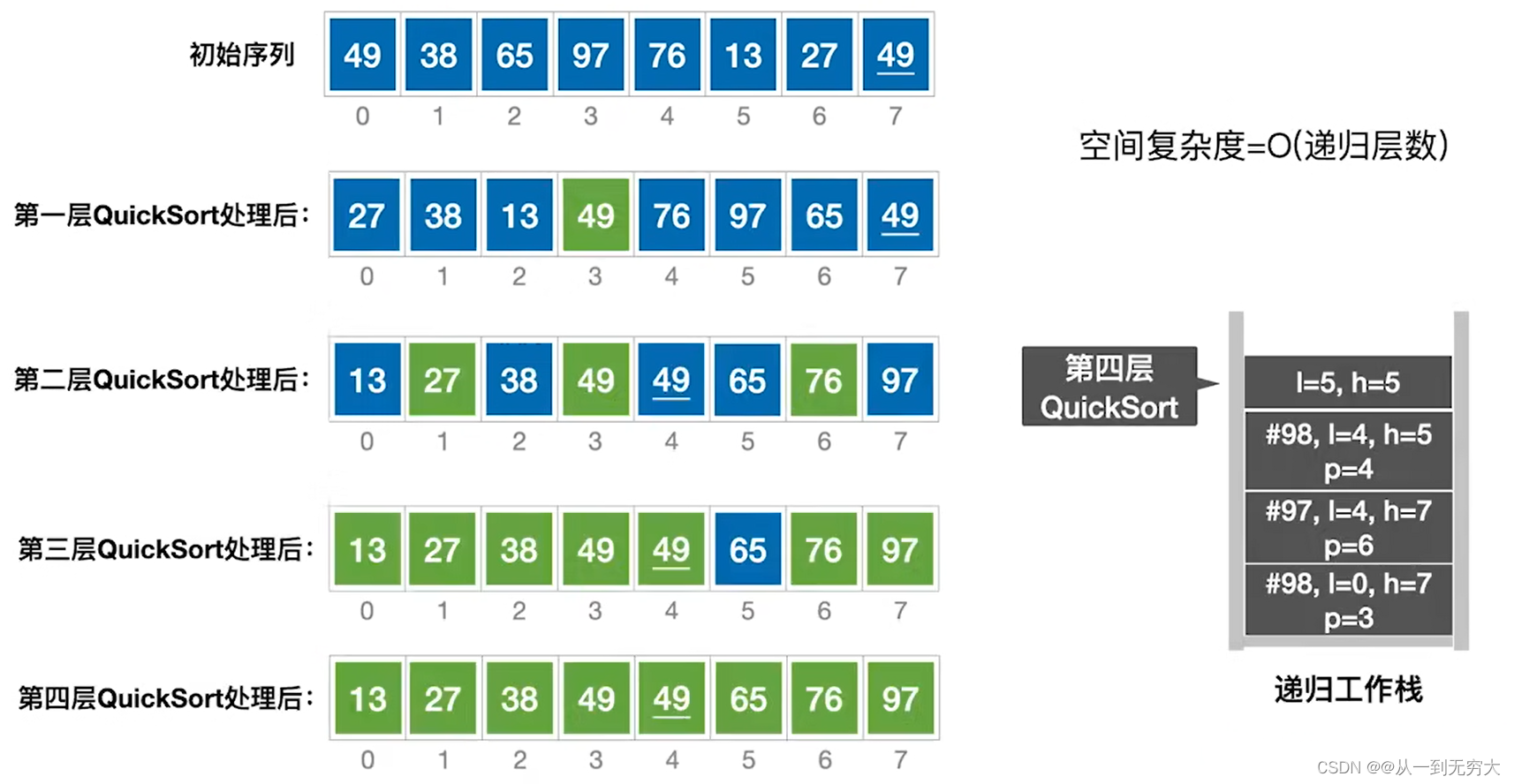
public static void quickSort(int[] arr, int left, int right){
if (left > right){
return;
}
int i = left;
int j = right;
int temp = arr[left];
while (i < j){
while (arr[j] >= temp && i < j){ // 从右向左找到第一个比基准值小的元素
--j;
}
while (arr[i] <= temp && i < j){ // 从左向右找到第一个比基准值大的元素
++i;
}
swap(arr, i, j);
}
// 交换基准值
arr[left] = arr[j];
arr[j] = temp;
quickSort(arr, left, j - 1);
quickSort(arr, j + 1, right);
}
5 归并排序
归并排序基本思想:归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略(分治法将问题分成一些小的问题然后递归求解,而治的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
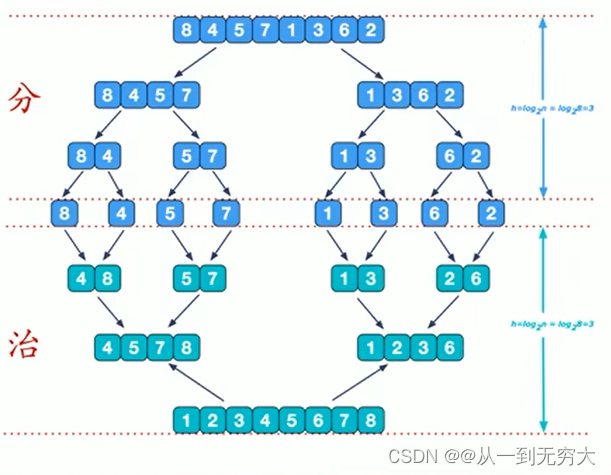
空间复杂度为O(n),来自于辅助数组。
public static void mergeSort(int[] arr, int left, int right, int[] temp){
if (left < right){
int mid = left + (right - left) / 2; // 中间索引
mergeSort(arr, left, mid, temp); // 向左递归进行分解
mergeSort(arr, mid + 1, right, temp); // 向右递归进行分解
merge(arr, left, mid, right, temp); // 合并
}
}
public static void merge(int[] arr, int left, int mid, int right, int[] temp){
int i = left; // 左侧区间的第一个数
int j = mid + 1; // 右侧区间的第一个数
int k = 0;
// 把左右两边(有序)的数据按照规则填充到temp数组,直到左右两边的有序序列一边处理完为止
while (i <= mid && j <= right){
if (arr[i] < arr[j]){
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
// 把有剩余数据的一边的数据依次填充到temp
while (i <= mid){
temp[k++] = arr[i++];
}
while (j <= right){
temp[k++] = arr[j++];
}
// 将temp数组的元素拷贝到arr
k = 0;
int t = left;
while(t <= right){
arr[t++] = temp[k++];
}
}
6 基数排序
基数排序基本思想:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
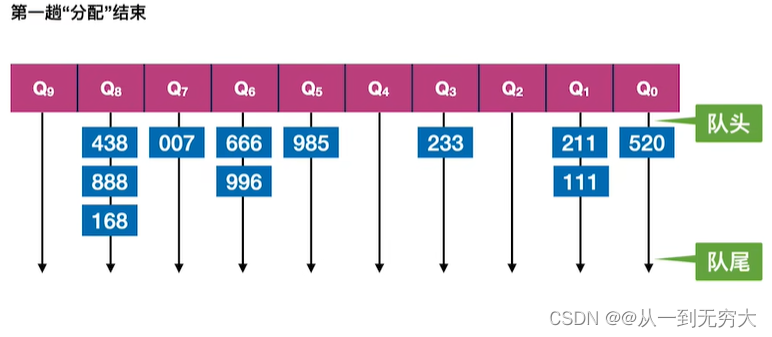
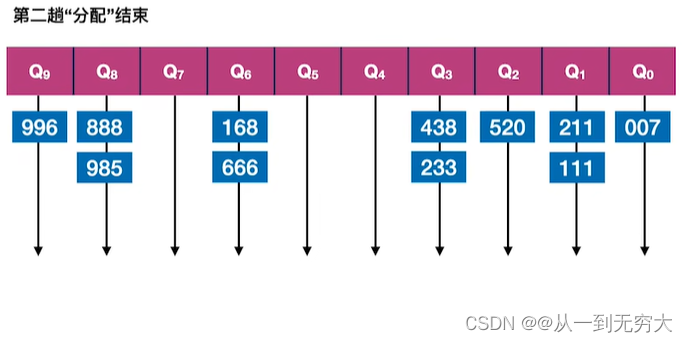
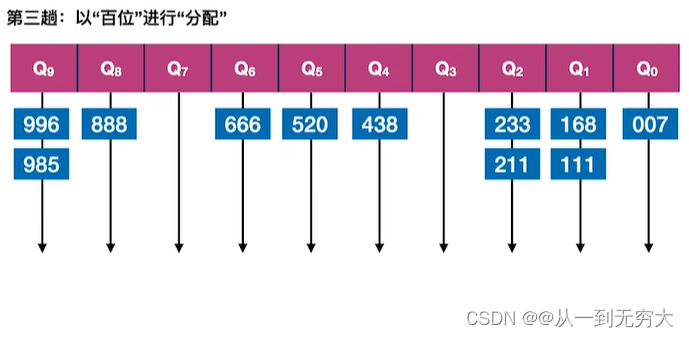
一趟分配O(n),一趟收集O( r),总共d趟分配、收集,总的时间复杂度为O(d(n+r));需要r个辅助队列,空间复杂度=O( r)。
public static int number(int[] arr){
int res = 0;
for (int i = 0; i < arr.length; ++i){
if (arr[i] > res){
res = arr[i];
}
}
return (res + "").length();
}
public static void radixSort(int[] arr){
int num = number(arr);
int[][] bucket = new int[10][arr.length]; // 一共建立10个桶
int[] bucketElement = new int[10]; // 记录每个桶的数据量
int index = 0;
for (int i = 0; i < num; ++i){
// 将数据放入桶中
for (int j = 0; j < arr.length; ++j){
int k = (int) (arr[j] / Math.pow(10, i) % 10);
bucket[k][bucketElement[k]] = arr[j];
++bucketElement[k];
}
// 将数据写回arr数组
for(int j = 0; j < 10; ++j){
int k = 0;
while (k < bucketElement[j]){
arr[index++] = bucket[j][k];
++k;
}
bucketElement[j] = 0;
}
index = 0;
}
}
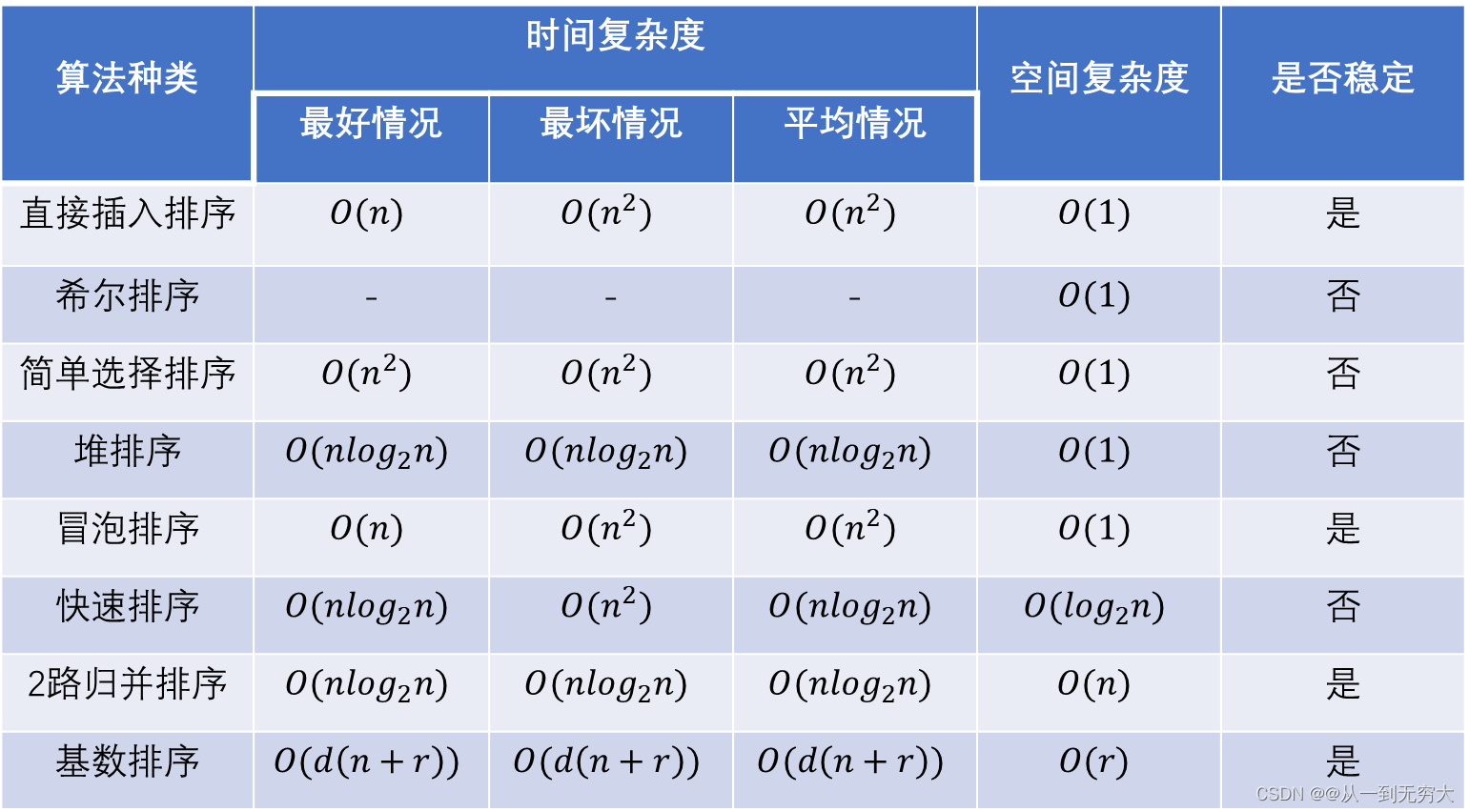
7 各种排序算法的性质
算法的稳定性
若待排序表中有两个元素Ri和Rj,其对应的关键字相同即keyi=keyj,且在排序前Ri在Rj的前面,若使用某一排序算法排序后,Ri仍然在Rj的前面,则称这个排序算法是稳定的,否则称这个排序算法是不稳定的。
参考:
https://www.bilibili.com/video/BV1E4411H73v?p=1&vd_source=ff364c22743db2666f3a26c417a3f759
https://www.bilibili.com/video/BV1b7411N798?p=1&vd_source=ff364c22743db2666f3a26c417a3f759