题目

32. 最长有效括号【困难】

题解

栈

括号问题的标答，用栈解决，但是如果用传统做法，挨个测试字符串的子串是否有效时间复杂度会达到 $O(n^3)$ ，通过不了所有测试用例，于是这道题改了栈的用法，始终保持栈底元素为已遍历元素中最后一个没匹配的右括号下标，但是如果字符串首个字符是‘（’，那么就不满足该条件，因此一开始入栈“-1”元素以保持统一

这道题的具体做法是：

遇到 ‘(’，下标入栈
遇到 ‘)’，栈顶元素先出栈，表示匹配了当前右括号，这时：
如果栈空，右括号下标入栈
如果栈不空，右括号下标-栈顶元素（剩余的不能匹配的）=以该右括号为结尾的最长有效括号长度

从前往后遍历字符串并更新答案即可

class Solution {
    public int longestValidParentheses(String s) {
        int n=s.length(),res=0;
        if(n<2)
            return 0;
        Stack<Integer>stack=new Stack<>();
        stack.push(-1);
        for(int i=0;i<n;i++){
            if(s.charAt(i)=='(')
                stack.push(i);
            else{
                stack.pop();
                if(!stack.empty())
                    //当前全部人数减去剩余无法配对的人数（单身）即res
                    res=Math.max(res,i-stack.peek());
                else   
                    stack.push(i);
            }
        }
        return res;
    }
}

时间复杂度： $O (n)$

空间复杂度： $O (n)$

动态规划

困难题怎么能少得了动态规划呢

状态定义：dp[i]以下标 i 字符结尾的最长有效括号的长度。
状态转移方程：

1）s[i]==‘)’ 并且 s[i-1]==‘(’：…()
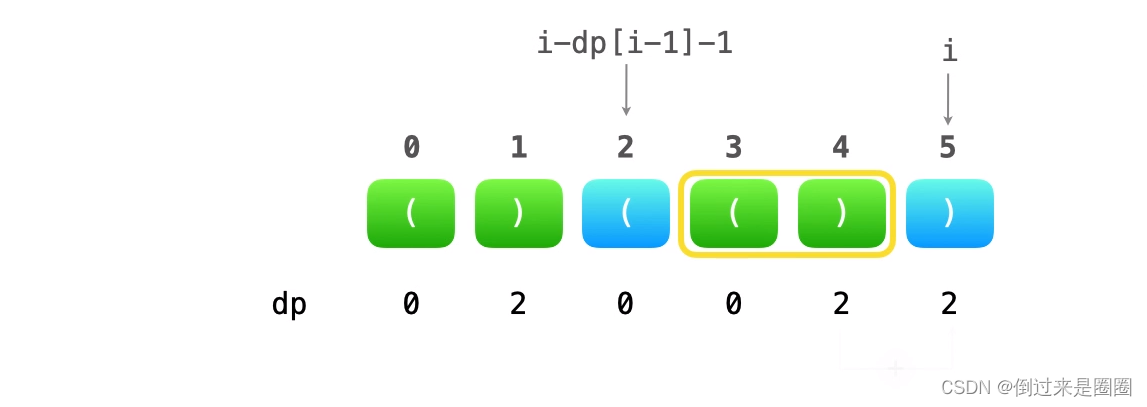
dp[i]=dp[i-2]+2
2）s[i]==‘)’ 并且 s[i-1]==‘)’：…))
s[i-dp[i-1]-1]==‘(’：dp[i]=dp[i-1] + dp[i-dp[i-1]-1] + 2
如果倒数第二个")“是有效括号sub的一部分，对于最后一个”)"，如果他是更长子串的一部分，则一定有一个对应的左括号。因此，如果sub前面刚好是一个左括号，就用2加上dp[i-1]（即sub的长度）更新dp[i]，然后sub之前的有效子串的长度也要加上，即dp[i-dp[i-1]-2]

初始条件：dp[i]=0
返回值：max(dp[i])

class Solution {
    public int longestValidParentheses(String s) {
        int n=s.length(),res=0;
        if(n<2)
            return 0;
        int[] dp=new int[n];
        for(int i=1;i<n;i++){
            if(s.charAt(i)==')'){
                //"()"
                if(s.charAt(i-1)=='(')
                    dp[i]=i-2>=0?dp[i-2]+2:2;
                //"))"
                else if(s.charAt(i-1)==')'){
                    //"(...))"
                    if(i-dp[i-1]-1>=0&&s.charAt(i-dp[i-1]-1)=='(')
                        dp[i]=dp[i-1]+2+(i-dp[i-1]>=2?dp[i-dp[i-1]-2]:0);
                }
            }
            res=Math.max(res,dp[i]);
        }
        return res;
    }
}

时间复杂度： $O (n)$

空间复杂度： $O (n)$

正向逆向结合法（不需要额外空间）

很巧妙的方法，需要遍历字符串两遍

从左向右遍历：
遇到“（”，left++；遇到“）”，right++；
如果left==right，计算当前有效括号长度，并更新最长的；
如果right>left，双方清零
从右向左遍历：
前两条类比相同
如果left>right，双方清零。这样是为了避免漏掉左括号始终比右括号多的情况，如(()

class Solution {
    public int longestValidParentheses(String s) {
        int n=s.length(),res=0,left=0,right=0;
        if(n<2)
            return 0;
        //从左向右遍历
        for(int i=0;i<n;i++){
            if(s.charAt(i)=='(')
                left++;
            else
                right++;
            
            if(left==right)
                res=Math.max(res,left+right);
            if(right>left){
                left=0;
                right=0;
            }
        }
        left=right=0;
        //从右向左遍历
        for(int i=n-1;i>=0;i--){
            if(s.charAt(i)=='(')
                left++;
            else
                right++;
            if(left==right)
                res=Math.max(res,left+right);
            if(left>right){
                left=0;
                right=0;
            }
        }
        return res;
    }
}