贪心算法
贪心算法(Greedy Algorithm)是一种
(1)在每一步选择中都采取在当前状态下的最优决策(局部最优)
(2)并希望由此导致的最终结果也是全局最优的算法
贪心算法与一般的搜索,以及后面要讲的动态规划相比,不同之处在于:它不对整个状态空间进行遍历或计算,而是始终按照局部最优选择执行下去,不再回头。
因为这个特性,贪心算法不一定能得到正确的结果
除非可以证明,按照适当的方法做出局部最优选择,依然可以得到全局最优结果
能用贪心求解的题目,也都可以用搜索或动态规划求解,但贪心一般是最高效的
引入:零钱兑换问题
322.零钱兑换
https://leetcode.cn/problems/coin-change/
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount+1,INT_MAX-1);
dp[0]=0;
for(int i=1;i<=amount;i++)
{
for(int j=0;j<coins.size();j++)
{
if(coins[j]<=i)
{
dp[i]=min(dp[i-coins[j]]+1,dp[i]);
}
}
}
dp[amount]=dp[amount]==INT_MAX-1?-1:dp[amount];
return dp[amount];
}
};
给一个硬币面额的可选集合coins,求拼成金额amount最少需要多少枚硬币。
例: coins = [20, 10, 5, 1], amount=46
答案: 46=20+20+5+ 1
零钱兑换:贪心
根据我们平时找钱的思路,一般我们会先考虑面值大的,零钱再用面值小的凑齐
“每次都选尽量大的面值”就是一个贪心思想
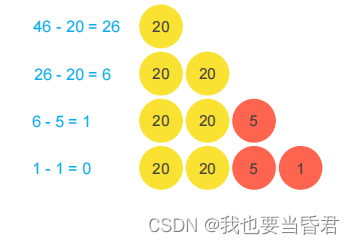
零钱兑换:贪心法的反例
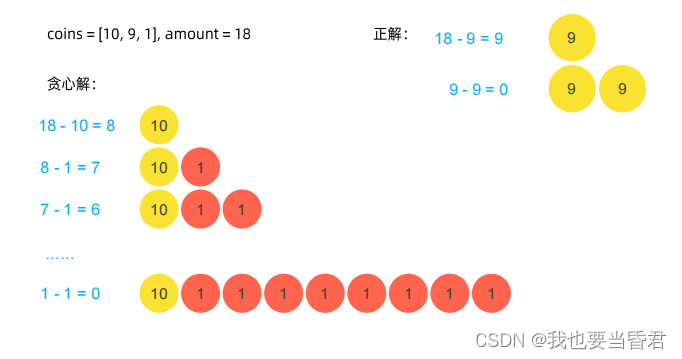
零钱兑换:搜索
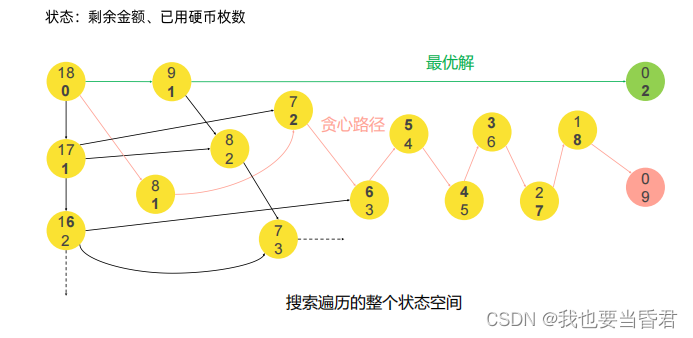
贪心算法的证明
由“零钱兑换"问题可以看出,贪心算法实际上是在状态空间中按局部最优策略找了一条路径。
贪心算法不一定能得出正确的解, 在大部分题目上不能随便使用。
遇到题目,一般先想搜索、动态规划等基于全局的解法,若时间复杂度太高,再考虑贪心。
若要使用贪心算法,必须先证明其正确性。
除了反证法、数学归纳法等大家熟悉的方法外,我们再介绍几种常用的手法。
实战
860.柠檬水找零
https://leetcode.cn/problems/lemonade-change/description/
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
coins[5] = coins[10] = coins[20] = 0;
for(int bill : bills) {
coins[bill]++;
if(!exchange(bill - 5)) return false;
}
return true;
}
private:
bool exchange(int amount) {
for(int x : {20, 10, 5}) {
while (amount >= x && coins[x] > 0) {
amount -= x;
coins[x]--;
}
}
return amount == 0;
}
unordered_map<int, int> coins;
};
“零钱兑换"类问题在面值互相构成倍数时,贪心算法成立
在本题中,面值为[5, 10, 20]
如果能用1个10块找零,那用2个5块必然也也可以
也就是说,做出“用10块找零”这个决策,未来的可能性包含了” 用2个5块找零”以后未来的可
能性一决策包容性
所以本题可以贪心:优先使用面值较大的找零
455.分发饼干
https://leetcode.cn/problems/assign-cookies/description/
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int candy=0,child=0;
while(child<g.size() && candy<s.size())
{
if(g[child]<=s[candy])
{
child++;
}
candy++;
}
return child;
}
};
两种思路
一块饼干(尺寸s[j]) 发给谁?发给满足g[i] <= s[j]的最大g[i] (刚刚好能满足的孩子)
一个孩子(胃口g[i])吃哪块饼干?吃满足s[j] >= g[i]的最小s[j],不存在就别吃了
通俗点讲就是小饼干给小孩子,大饼干给大孩子,不能满足就不给了
决策包容性: -块饼干总是想要满足一一个孩子的,满足胃口更大的孩子,未来的可能性包含了满足
胃口更小孩子的可能性
把饼干和孩子排序,代码更容易实现
贪心算法的证明
决策范围扩展
在思考贪心算法时,有时候不容易直接证明局部最优决策的正确性
此时可以往后多扩展一一步, 有助于对当前的决策进行验证
实战
122.买卖股票的最佳时机II
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
for(int i = 1; i < prices.size(); i++){
ans += max(prices[i] - prices[i - 1], 0);
}
return ans;
}
};
这是一个预言家的炒股状态一知道未来每 天的价格
当前持有股票,卖不卖?往后看一天,明天还涨那肯定不卖,明天跌那肯定卖啊!
当前没有股票,买不买?往后看一天,明天涨那肯定买,明天跌那肯定先不买!
最后就是完美结果一获得所有 prices[i]- prices[i- 1]> 0区间的收益
45.跳跃游戏II
https://leetcode.cn/problems/jump-game-ii/
class Solution {
public:
int jump(vector<int>& nums) {
int now = 0;
int ans = 0;
while (now < nums.size() - 1) {
int right = now + nums[now];
if (right >= nums.size() - 1) return ans + 1;
int nextRight = right;
int next = now;
for(int i = now + 1; i <= right; i++) {
if(i + nums[i] > nextRight) {
nextRight = i + nums[i];
next = i;
}
}
now = next;
ans++;
}
return ans;
}
};
看一下往后跳两步的所有可能性
贪心策略:若a能到b1, b2,b3,而b1, b2, b3能到的最远位置分别为C1, c2, c3,那应该从a
跳到c1, c2 ,c3中最大的一个对应的b。
Leetcode示意图
决策包容性:同样都是跳1步,从a跳到“能跳得更远”的b,未来的可达集合包含了跳到其他
b的可达集合,所以这个局部最优决策是正确的。
邻项交换
经常用于以某种顺序“排序”为贪心策略的证明
证明在任意局面下,任何局部的逆序改变都会造成整体结果变差
实战
1665.完成所有任务的最少初始能量
https://leetcode.cn/problems/minimum-initial-energy-to-finish-tasks/
class Solution {
public:
int minimumEffort(vector<vector<int>>& tasks) {
sort(tasks.begin(), tasks.end(),
[](const vector<int>& a, const vector<int>& b) {
return a[0] - a[1] < b[0] - b[1];
});
int ans = 0;
for(int i = tasks.size() - 1; i >= 0; i--) {
ans = max(tasks[i][1], ans + tasks[i][0]);
}
return ans;
}
};
考虑任意一种做任务的顺序, 设做完第i+2到n个任务所需的初始能量最少为S
对于两个相邻任务:设第i个和第i+1个完成的任务分别是p和q

先做p,所需初始能量为: max(max(minimum[q], S+actual[q])+actual[p], minimum[p])
先做q,所需初始能量为: max(max(minimum[p], S+actual[p])+actual[q], minimum[q])
若先做p比较优,则应满足(拆括号,消去一样的项)
max(minimum[q] + actual[p], minimum[p]) < max(minimum[p] + actual[q], minimum[q)
因为必定有minimum[q] + actual[p] > minimum[q]
所以上式等价于minimum[q] + actual[lp] < minimum[p] + actuallq]
即actual[p] - minimum[p] < actual[lq] - minimum[q]
贪心策略:按照actual - minimum升序排序,以此顺序完成任务
推荐一个零声学院免费公开课程,个人觉得老师讲得不错,分享给大家:Linux,Nginx,ZeroMQ,MySQL,Redis,fastdfs,MongoDB,ZK,流媒体,CDN,P2P,K8S,Docker,TCP/IP,协程,DPDK等技术内容,立即学习