[数据结构与算法][数据结构]~堆

前言

作者：小蜗牛向前冲

名言：我可以接收失败，但我不能接收放弃

?如果觉的博主的文章还不错的话，还请点赞，收藏，关注👀支持博主。如果发现有问题的地方欢迎?大家在评论区指正。

目录

?一 堆

?二 堆的实现

1 堆实现的功能

2 向上调整算法和向下调整算法

3 实现堆

三 堆的应用

1 堆排序?

2 TOP-K问题

?一 堆

1 堆的概念

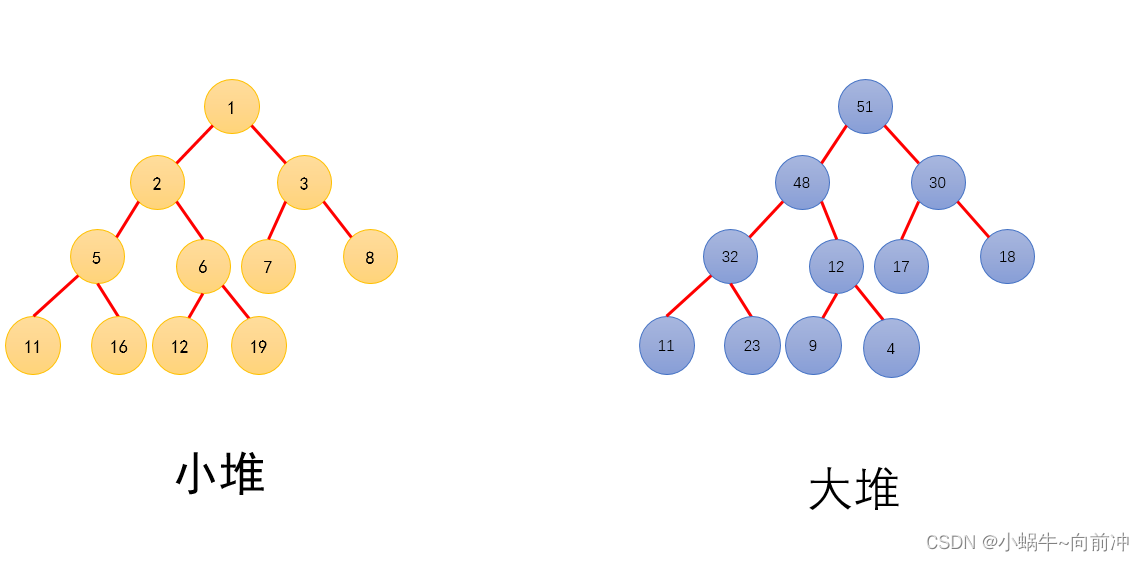
? 有一组数据，我们将他们用完全二叉树的方式储存在一个一维数组中，并满足一定规律。 则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

?2 堆的性质

堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

这里我们要区分堆在逻辑上是个树的形状，但是在物理层面上是挨着存储的。?

?二 堆的实现

1 堆实现的功能

对于堆来是一般要实现入堆和出堆的功能,这里我们对于堆的建立很像顺序表，但他们仍然是有很大区别的，下面大家可以在堆的实现过程中细细体会。

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int HPDataType;

//定义堆
typedef struct heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

//打印
void HeapPrint(HP* php);
//初始化
void HeapInit(HP* php);
//销毁堆
void HeapDestroy(HP* php);
// 入堆
void HeapPush(HP* php, HPDataType x);
// 出堆顶元素
void HeapPop(HP* php);
// 返回堆顶元素
HPDataType HeapTop(HP* php);
//判断堆是否为空
bool HeapEmpty(HP* php);
//求堆的大小
int HeapSize(HP* php);
//向上调整
void ADjustDown(HPDataType* a, int n, int parant);
//向下调整
void ADjustUp(HPDataType* a, int child);
//交换
void swop(int* p1, int* p2);

2 向上调整算法和向下调整算法

在这里我们先来了解堆调整的二种算法：

向上调整算法

我们先说一个结论：

数组小标计算父子关系公式：

parant = (child-1)/2;

LeftChild = parant*2+1;? ? ? 奇数

RightChild = parant*2+2;? ??偶数? ? ??

好我们知道了，这个公式我们就可以通过数组建树?，至于如何建堆，下面在说，我们继续可看到向上调整算法。

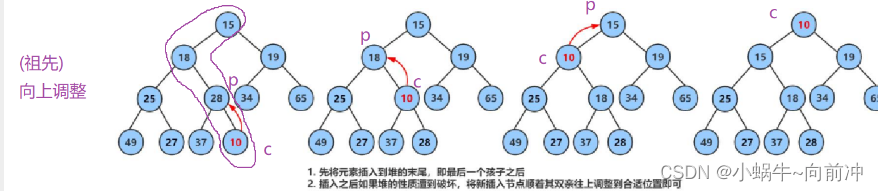我们知道是通过数组来建堆，我们要插入一个数据，直接插入到数组的后一个元素这肯定是不符合堆的规则的，那么我们可以用向上调整算法来进行调整，调整的方式见上图（小堆）。?

下面我们用代码来实现一下：

/向上调整
void ADjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//小堆
		if (a[parent] > a[child])
		{
			//交换
			swop(&a[parent], &a[child]);
		}
		else
		{
			break;
		}
		//向上调整
		child = parent;
		parent = (child - 1) / 2;
	}
}

那么我们在来思考一下，该算法的时间复杂度为都少呢？

假设我们认为数有N层，我们入堆一个数，最坏的结果是N-1次也就是，该算法的时间复杂度为O(N)。

向下调整算法

这个算法我们可用来解决出堆的问题，为什么这么说呢？因为每次我们出堆，我们都要保持堆的结构的完整性，那么我们就要选出最小或者最大的数做堆顶。

当我们要出堆时，只要让数组的首元素和最后的元素交换，在size--,在用向下调整算法就可以保持堆的结构的父子关系。

该算法的核心就是当在交换后，让首元素(父节点)和最小的子节点交换，以次类推得到小堆。

要想得到大堆只要改变：

?把a[minChild]<a[parant]变为a[minChild]>a[parant]即可。

代码实现如下：

void ADjustDown(HPDataType*a,int n,int parant)
{
	int minChild = parant * 2 + 1;
	//找出最小的孩子
	while (minChild < n)
	{
		if (minChild + 1 < n && a[minChild] > a[minChild + 1])
		{
			minChild++;
		}
		if (a[minChild] < a[parant])
		{
			//交换
			swop(&a[parant], &a[minChild]);
			parant = minChild;
		minChild = parant * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

那该算法的时间复杂度又是多少呢？

我们假设该树有N层，总节点数为n：

第1层：有2^0个节点

第2层：有2^1个节点

第3层：有2^2个节点

…………………………

第N层:有2^(N-1)个节点

从中可以看出这就是个等比数列，所以我们直接通过公式求和：

T(N)=2^N-1,对于该算法最坏的结果就是每层都要调整，则n = 2^N-1，所以时间复杂度为

N = log(n+1),即为O(logn)

综上说：

向上调整算法的时间复杂度为O(n),而向下调整法的时间复杂度为O(logn),也就是向下调整算法的效率是更高的。

3 实现堆

堆的初始化

//初始化堆
void HeapInit(HP* php)
{
	assert(php);//断言
	php->a = NULL;
	php->size = php->capacity = 0;
}

在入堆和出堆的过程中我们都次要用到交换这个功能，所以我们在这里去实现个交换功能

//交换
void swop(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

堆的销毁

//堆的销毁
void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

?入堆

这里用到了向上调整算法，上面我们知道向下调整算法是比向下调整更优的，所以说我们这里是可以改进的。

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	//扩容
	if (php->size == php->capacity)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType*) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	//插入
	php->a[php->size] = x;
	php->size++;
	//向上调整保持堆的形状
	ADjustUp(php->a, php->size - 1);
}

出堆顶元素

//出堆顶元素
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	//交换
	swop(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	//向下调整
	ADjustDown(php->a,php->size,0);
}

返回堆顶元素

//返回堆顶元素
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}

判断堆是否为空

bool HeapEmpty(HP* php)
{
	assert(判断堆是否为空php);
	return php->size == 0;//为空返回true,不为空返回flase
}

返回堆的长度

//返回堆的长度
int HeapSize(HP* php)
{
	assert(php);
	return php->size - 1;
}

完整实现：

#define  _CRT_SECURE_NO_WARNINGS

#include"heap.h"

//打印堆
void HeapPrint(HP* php)
{
	assert(php);
	int i = 0;
	while (php->size > i)
	{
		printf("%d ", php->a[i]);
		++i;
	}
	printf("\n");
}

//初始化堆
void HeapInit(HP* php)
{
	assert(php);//断言
	php->a = NULL;
	php->size = php->capacity = 0;
}

//交换
void swop(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
//向上调整
void ADjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//小堆
		if (a[parent] > a[child])
		{
			//交换
			swop(&a[parent], &a[child]);
		}
		else
		{
			break;
		}
		//向上调整
		child = parent;
		parent = (child - 1) / 2;
	}
}

//堆的销毁
void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}
// 入堆
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	//扩容
	if (php->size == php->capacity)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType*) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	//插入
	php->a[php->size] = x;
	php->size++;
	//向上(或者向下)调整保持堆的形状
	ADjustDown(php->a, php->size, 0);
}
void ADjustDown(HPDataType*a,int n,int parant)
{
	int minChild = parant * 2 + 1;
	//找出最小的孩子
	while (minChild < n)
	{
		if (minChild + 1 < n && a[minChild] > a[minChild + 1])
		{
			minChild++;
		}
		if (a[minChild] < a[parant])
		{
			//交换
			swop(&a[parant], &a[minChild]);
			parant = minChild;
		minChild = parant * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//出堆顶元素
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	//交换
	swop(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	//向下调整
	ADjustDown(php->a,php->size,0);
}

//返回堆顶元素
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}
//判断堆是否为空
bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;//为空返回true,不为空返回flase
}
//返回堆的长度
int HeapSize(HP* php)
{
	assert(php);
	return php->size - 1;
}

三 堆的应用

对于堆来是主要用途：

堆排序
解决TOP-K问题

1 堆排序?

为什么说堆可用来排序呢？我们知道堆顶一定是这堆中最大数或者最小数，所以我们可以利用这一特性进行排序。

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

建堆

升序：建大堆

降序：建小堆

?对于建堆来说，我们可以去写一个堆，但这样太麻烦了，我们可以直接通过向下调整算法建堆。

我们假设树的高度为h

第1层，2^0个节点，需要向下移动h-1层

第2层，2^1个节点，需要向下移动h-2层

第3层，2^2个节点，需要向下移动h-3层

第4层，2^3个节点，需要向下移动h-4层

………………………………………………
第h-1层，2h-2个节点，需要向下移动1层

调整次数 = 每一次层节点个数*这层最坏向下调整的次数

我们建堆的时间复杂度我们可以通过计算得：

?所以说向下调整建堆的时间复杂度为O(N)。

?利用堆删除思想来进行排序

其实就是建堆尾和堆头交换，后通过向下调整算法，将最大数或者最小数倒序排出。

?完整代码：

//思路：依次选择数，从后往前排
// 升序------大堆
// 降序------小堆
//堆排
void HeapSort(int* a, int n)
{
	//从下调整建堆
	for (int i = (n - 2) / 2;i >= 0;--i)
	{
		ADjustDown(a, n, i);
	}
	//交换，选数
	int i = 1;
	while (i < n)
	{
		swop(&a[0], &a[n - i]);
		ADjustDown(a, n - i,0);
		++i;
	}
}

2 TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

如求世界最高10人的身高，我们第1个想法是世界上所以的人的身高都排序个序，但这样是不是代价太大了，那我们有没有更加简单的方法呢？这将可以用到我们的堆了。

用数据集合的前K个元素来建堆：

前K个最大元素，建小堆

前K个最小元素，建大堆

堆中选数

用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

完整代码：

#define  _CRT_SECURE_NO_WARNINGS

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<time.h>

typedef int HPDataType;

//定义堆
typedef struct heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

//交换
void swop(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//向下调整算法
void ADjustDown(HPDataType* a, int n, int parant)
{
	int minChild = parant * 2 + 1;//默认左孩子是最小
	//找出最小的孩子
	while (minChild < n)
	{
		if (minChild + 1 < n && a[minChild] > a[minChild + 1])
		{
			minChild++;
		}
		if (a[minChild] < a[parant])
		{
			//交换
			swop(&a[parant], &a[minChild]);
			parant = minChild;
			minChild = parant * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//创建数据
void CreateDataFile(const char* filename, int N)
{
	//以写入的方式打开文件
	FILE* fin = fopen(filename, "w");
	if (NULL==fin)
	{
		perror("fopen fail");
		return;
	}
	srand(time(0));
	//写入数据
	for (int i = 0;i < N;++i)
	{
		fprintf(fin, "%d\n", rand() % 1000000);
	}
	fclose(fin);
}
//TOP前10位数
void PrintTopK(const char* filename, int k)
{
	assert(filename);
	//打开文件
	FILE* fout = fopen(filename, "r");
	if (NULL==fout)
	{
		perror("fopen fail");
		return;
	}
	//为堆分配空间
	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (NULL == minHeap)
	{
		perror("malloc fail");
		return;
	}
	//读取前K个元素
	for (int i = 0;i < k;++i)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}
	//建出小堆
	for (int i = (k - 2) / 2; i >= k;--i)
	{
		ADjustDown(minHeap, k, i);
	}
	//比较后N-K个元素比堆顶元素大的就入堆
	int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{
		if (val > minHeap[0])
		{
			minHeap[0] = val;
			ADjustDown(minHeap, k, 0);
		}
	}
	//打印排序结果
	for (int i = 0;i < k;++i)
	{
		printf("%d ", minHeap[i]);
	}
	//释放空间
	free(minHeap);
	//关闭文件
	fclose(fout);

}
int main()
{
	const char* filename = "Date.txt";
	int N = 1000000;
	int k = 10;
	//CreateDataFile(filename, N);
	PrintTopK(filename, k);
	return 0;
}

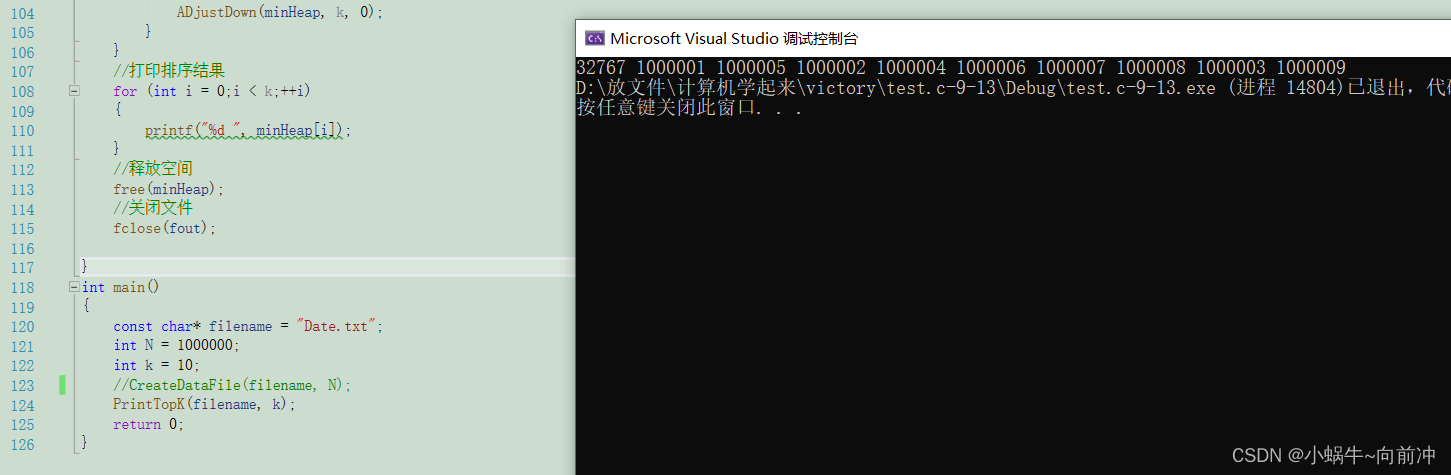
?在这里博主遇到了一个BUG想了很久，想和大家分享一下；

报了个断错误，我调试到90行代码时报错，我想这里这么会错误，断错误一般是传了个空参数

，我一想我就往上看，看一眼(我没错啊，我这么会错呢），就这样倒腾了半天。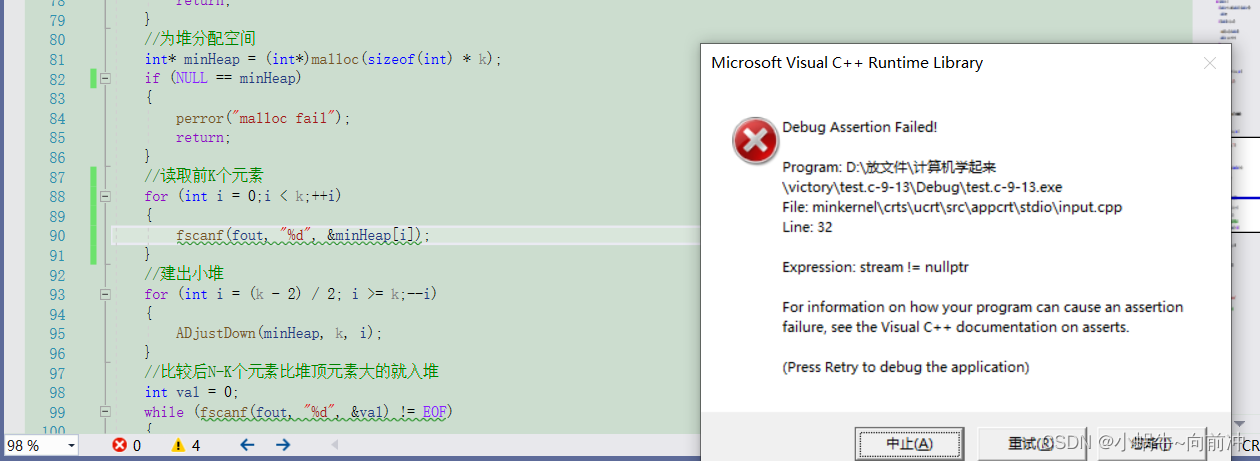

?突然发现，自己将fout置空了。

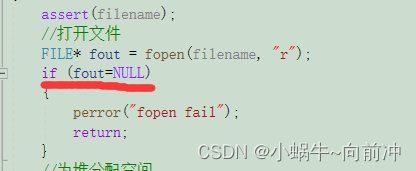
?这样的问题大家都有遇到到吧！那我们有上面方式避免吗？

其实有的，我们可以这样写。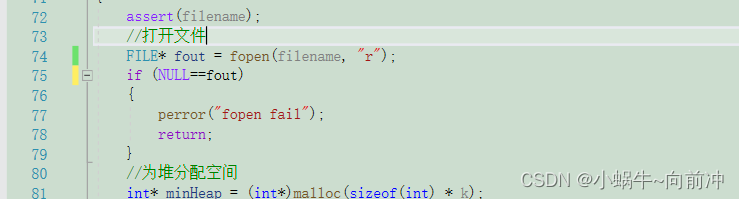

?如果我们仍然把等于(==)写成了赋值(=)会这么样呢？

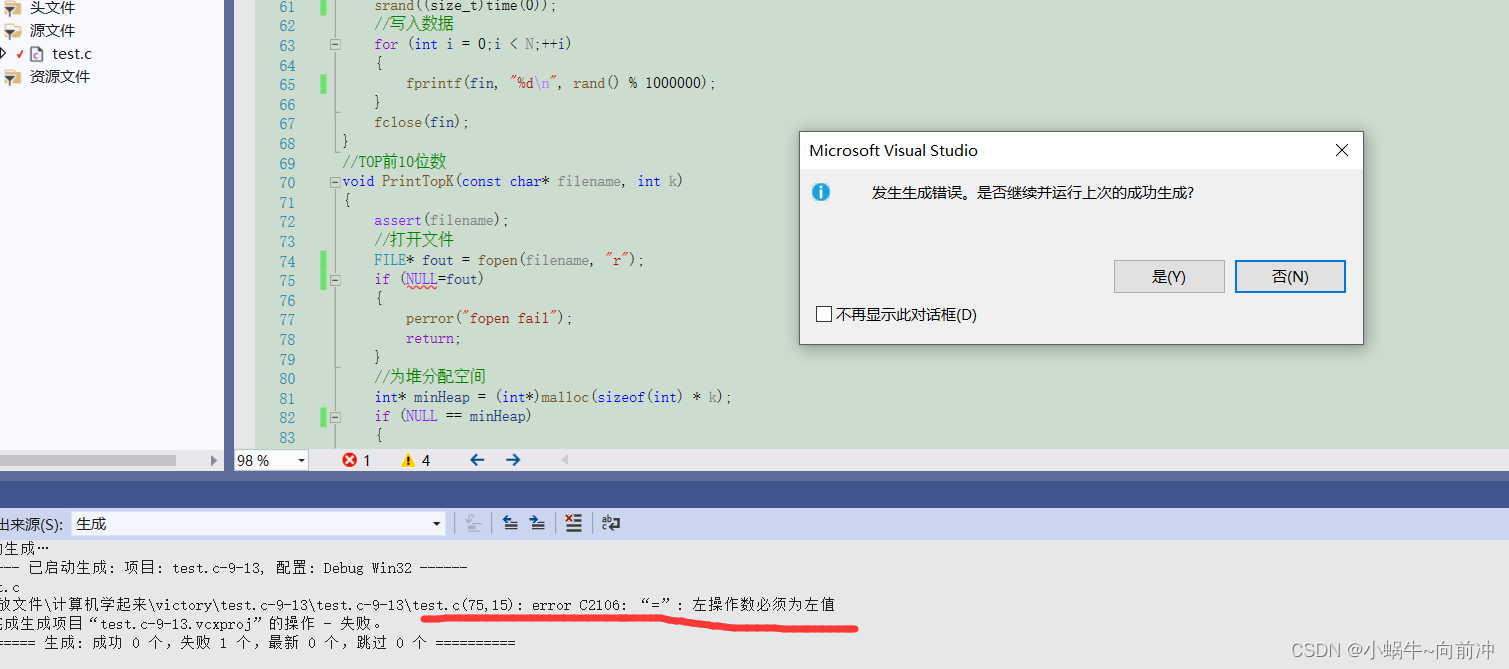
这样编译就不会通过，这样我就能及时是发现问题并解决。