二叉树递归套路序
判断一颗二叉树是否是完全二叉树
分如下四种情况:
1、首先以x为头的数它的左边和右边子树都是满的,且高度一样,则X为头的二叉树既是完全二叉树也是
满二叉树。
2、如果左树是完全二叉树,且右树是满二叉树那么左树高度比右树高度大1个,那么则是完全二叉树,
这种情况如下图所示:
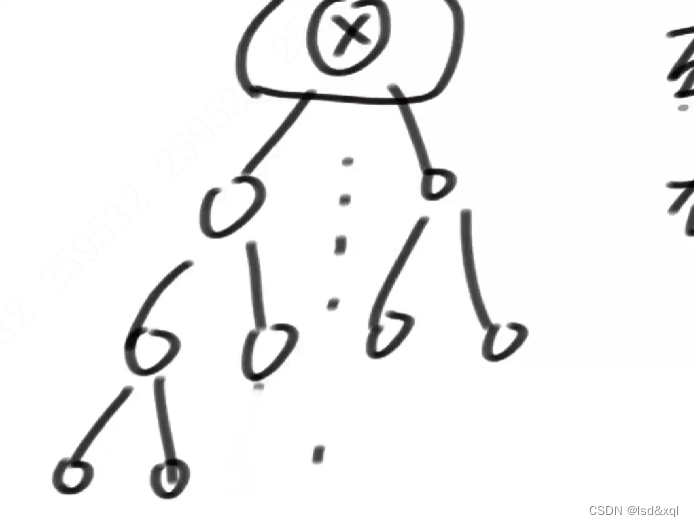
3、左树是满的并且右树是满的,我左树高度比右树高度大1个,那么也是一颗完全二叉树,这种情况如下图所示:
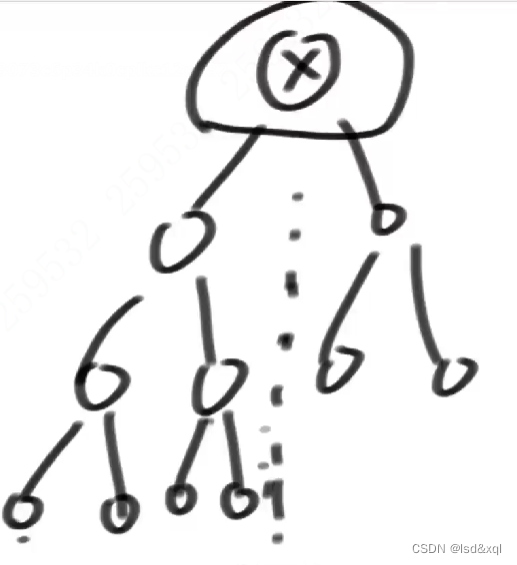
4、左树是满二叉树,右树是完全二叉树,如果两树高度相等,则是完全二叉树:
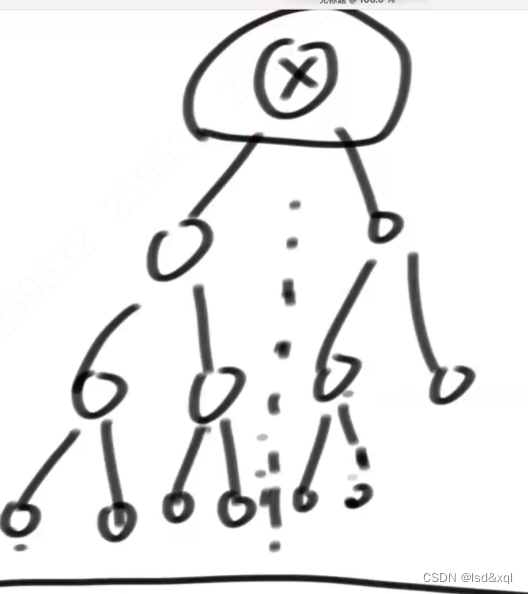
需要获取的信息体:
我需要拿到的信息是
左树是否满右树是否满,
左树是否是完全,右树是否是完全,
左树高度和右树高度
代码如下:
public static class Info {
//是否满二叉树
public boolean isFull;
//是否完全二叉树
public boolean isCBT;
public int height;
public Info(boolean isFull, boolean isCBT, int height) {
this.isFull = isFull;
this.isCBT = isCBT;
this.height = height;
}
}
public static boolean isCBT2(Node head) {
return process(head).isCBT;
}
public static Info process(Node x) {
if (x == null) {
return new Info(true, true, 0);
}
Info leftInfo = process(x.left);
Info rightInfo = process(x.right);
//左树满和右树满
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
boolean isFull = leftInfo.isFull && rightInfo.isFull
&& leftInfo.height == rightInfo.height;
boolean isCBT = false;
//可能性1
if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height) {
isCBT = true;
}
//可能性2
if (leftInfo.isCBT && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
isCBT = true;
}
//可能性3
if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height + 1){
isCBT = true;
}
//可能性4
if (leftInfo.isFull && rightInfo.isCBT && leftInfo.height == rightInfo.height) {
isCBT = true;
}
return new Info(isFull, isCBT, height);
}
给定一颗二叉树的头节点head,和另外两个节点a和b,返回a和b的最低公共祖先
两个节点同时往上跑,是在哪个节点上最初汇聚的,汇聚的点就是公共祖先节点。
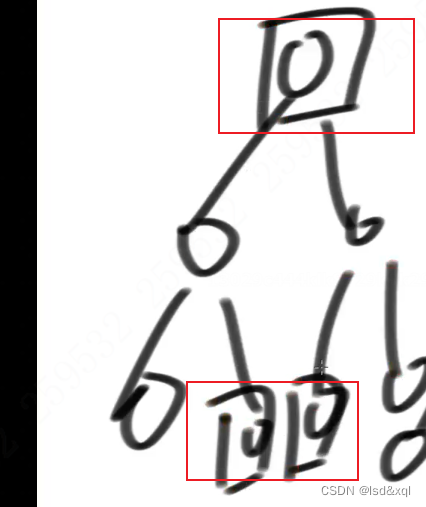
这种情况最低公共祖先在a:
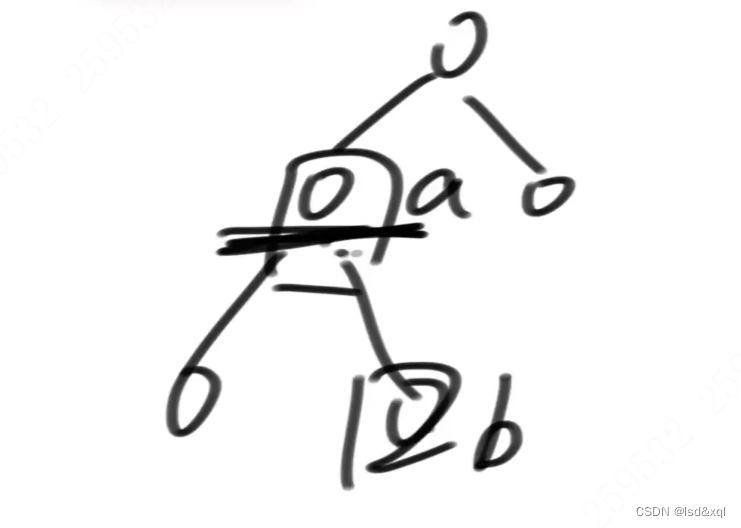
解法一:
生成一个map记录任何一个节点的父是谁,然后将a的节点向上找的各个节点全放在一个
set里面,然后b在往上找,直到b往上找的元素出现在set里面,那么这个元素就是最低公共祖先
节点。
二叉树递归套路解法:
x这颗树上a和b汇聚在哪,如果x这棵树上a和b没有汇聚,那么则返回null,
如果a和b有汇聚节点,则将这个节点返回。
判断以x为头的节点是否发现a,并且也要判断是否发现了b。
总结出:
汇聚点和X无关(X不是最低汇聚点)
(1)左树上面有答案
(2)右树上面有答案
(3)a,b没有找全
汇聚点和X有关
(1)左树发现了a,b任意个,右树发现了a,b任意一个
(2)X本身是a节点,左树或者右树发现了b
(3)X本身是b节点,左树或者右树发现了a
需要的信息:
1、树上是否发现a
2、树上是否发现b
3、树上是否发生汇聚
public static Node lowestAncestor2(Node head, Node a, Node b) {
return process(head,a,b).ans;
}
public static class Info {
public boolean findA;
public boolean findB;
public Node ans;
public Info(boolean findA, boolean findB, Node ans) {
this.findA = findA;
this.findB = findB;
this.ans = ans;
}
}
public static Info process(Node x, Node a, Node b) {
if (x == null) {
return new Info(false, false, null);
}
Info leftInfo = process(x.left, a, b);
Info rightInfo = process(x.right, a, b);
//自己再搜集三个信息
boolean findA = (x == a) || leftInfo.findA || rightInfo.findA;
boolean findB = (x == b) || leftInfo.findB || rightInfo.findB;
Node ans = null;
//左树上找到答案了,那么则直接将当前的答案赋值
if (leftInfo.ans != null) {
ans = leftInfo.ans;
} else if (rightInfo.ans != null) {
ans = rightInfo.ans;
} else {
//既找到了A又找到了B那么答案就是我自己
if (findA && findB) {
ans = x;
}
}
return new Info(findA, findB, ans);
}
派对的最大快乐值
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每个员工都有一个或多个直接下级。
这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则:
1.如果某个员工来了,那么这个员工的所有直接下级都不能来【直接上下级不要在一起】
2.派对的整体快乐值是所有到场员工快乐值的累加
3.你的目标是让派对的整体快乐值尽量大给定一棵多叉树的头节点boss,请返回派对的最大快乐值。
如下给17和20发请柬,最大happy值为37
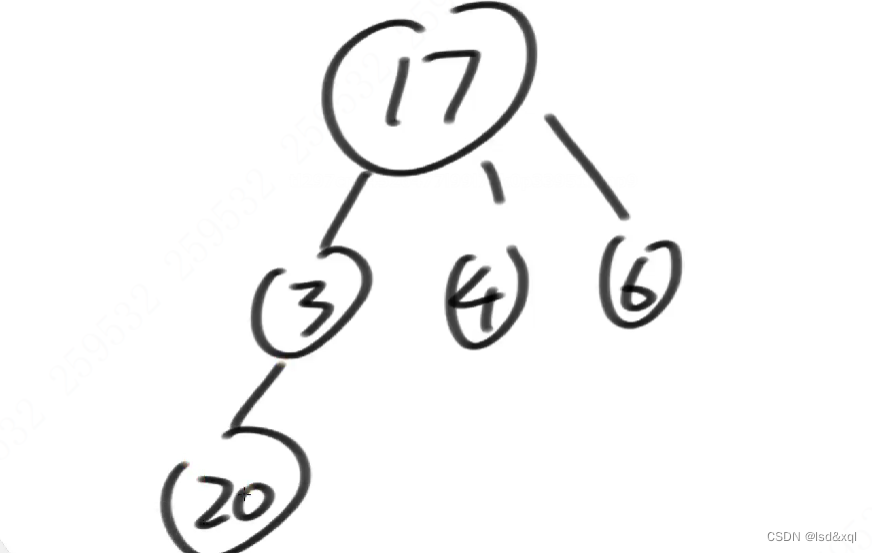
列可能性:
以X为头的多岔树
1、X来
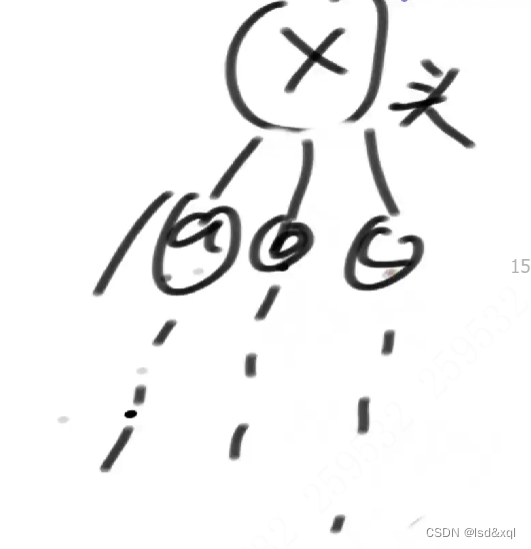
(1)X自己的快乐值加上a不来情况下最大收益加上b不来情况下的最大收益,加上c不来情况下的最大收益。
2、X不来
(1)0+a来或不来的情况下最大+b来或不来的情况下最大+c来或不来的情况下最大
public static class Employee {
public int happy;
public List<Employee> nexts;
public Employee(int h) {
happy = h;
nexts = new ArrayList<>();
}
}
public static int maxHappy2(Employee head) {
Info allInfo = process(head);
return Math.max(allInfo.no, allInfo.yes);
}
public static class Info {
//x不来
public int no;
//x来
public int yes;
public Info(int no, int yes) {
this.no = no;
this.yes = yes;
}
}
public static Info process(Employee x) {
if (x == null) {
return new Info(0, 0);
}
int no = 0;
//来提前获取一个happy
int yes = x.happy;
for (Employee next : x.nexts) {
Info nextInfo = process(next);
yes += nextInfo.no;
//我后代可以来或者可以不来
no += Math.max(nextInfo.no, nextInfo.yes);
}
return new Info(no,yes);
}
贪心算法
介绍:
(1)最自然智慧的算法
(2)用一种局部最功利的标准,总是做出在当前看来最好的选择
(3)难点在于证明局部最功利的标准可以得到全局最优解
(4)对于贪心算法的学习主要以增加阅历和经验为主
题目:
给定一个由字符串组成的数组strs,必须把所有的字符串拼接起来,返回所有可能的拼接结果中
,字典序最小的结果
首先得出贪心的思路是:
有a,b两个字符串,如果a concat b 小于b concat a,那么可以得出把a放前面,否则把b放前面。
首先证明:
我们的排序是有传递性的【为了证明这种策略下得到的结果是唯一的】:
1、不如说有三个整形遍历,a,b,c,如果a<b 并且b<c 那么一定能够得到a<c【这就是传递性】
换言之我们这里就是要推出:
a拼接上b小于等于b拼接上a
b拼接上c小于等于c拼接上b
从而推出
a拼接上c小于等于c拼接上a,这样才能证明其传递性
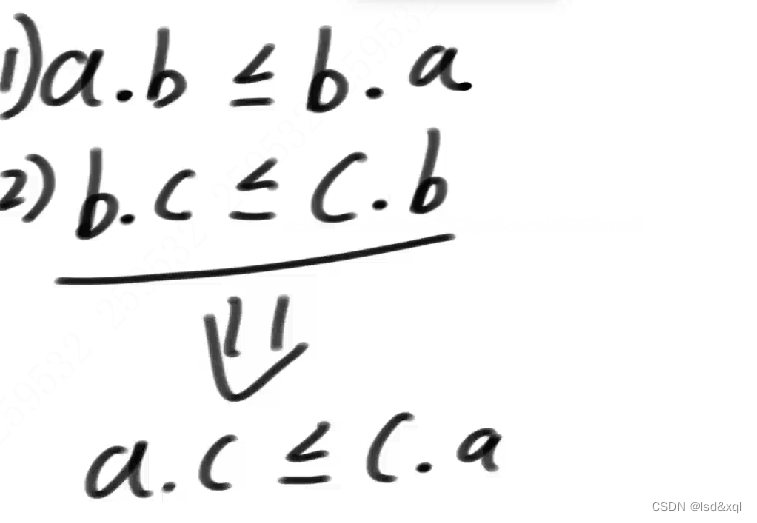
我们把拼接的过程抽象成一个k进制:
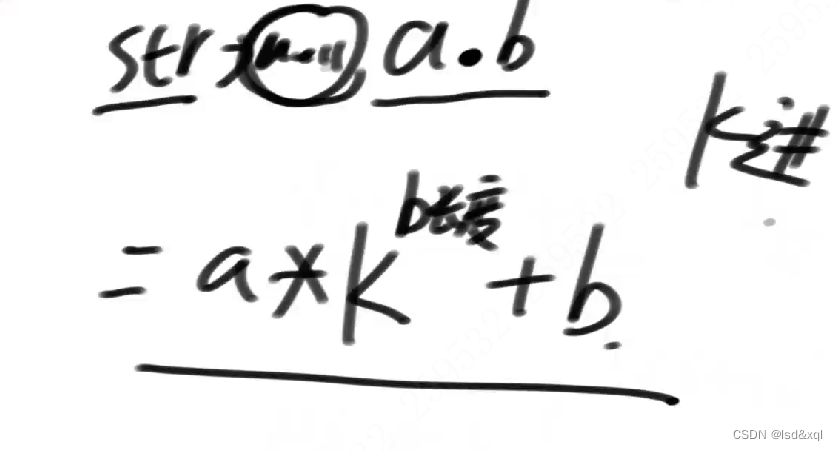
再把k的x次方抽象为一个m(x)方法:
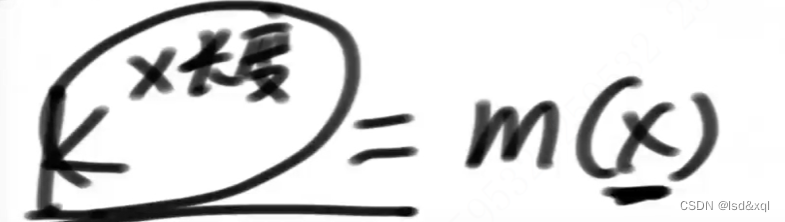
得到如下式子:
a.b <= b.a -> am(b)+b<=bm(a)+a
b.c <= c.b -> bm?+c<= cm(b)+b
将第一个式子乘以一个c,第二个式子乘以一个a
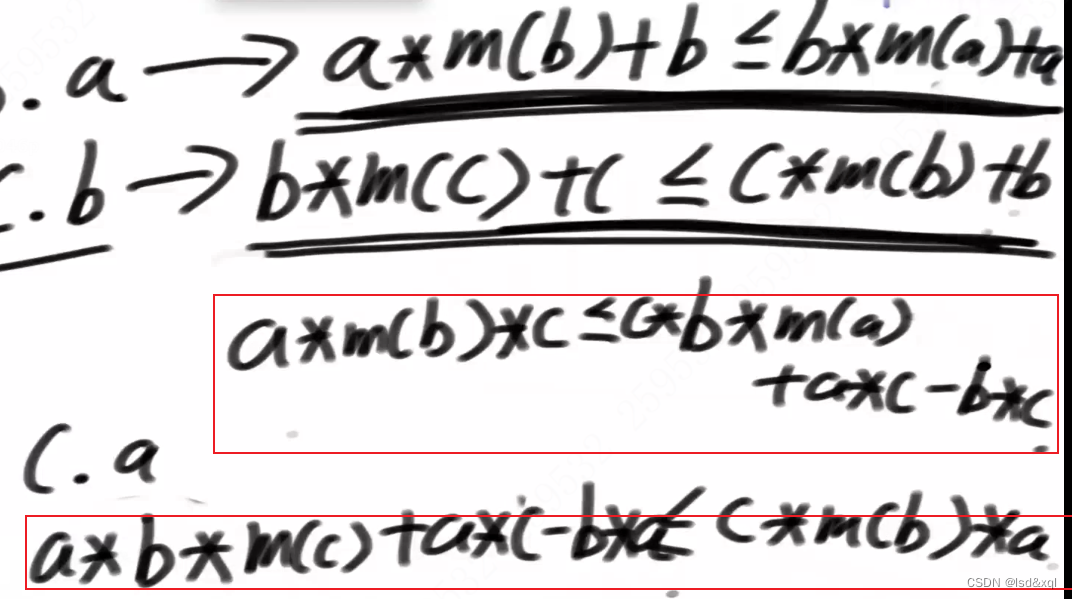
由于以上式子am(b)c是一样的,则就可以将两个式子给连起来了:
**cbm(a)+ac-bc>= abm?+ac-ba**
化简:
cbm(a)-bc>= abm?-ba
得到如下式子:
cm(a)-c>= am?-a
a.c<=c.a
至此传递性证明完毕。
2、证明整体字典序最小
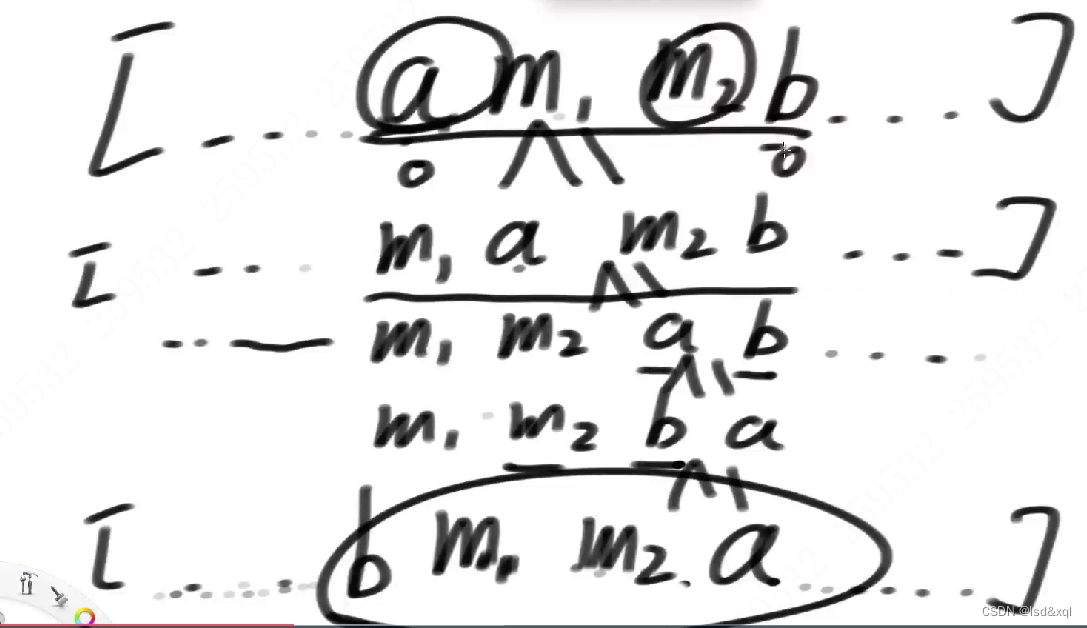
假设a是某一个在前的字符串,b是某一个在后的字符串,并且按照我的策略已经排完了。

如下图:
a和b之间有字符串数组m1和m2,如何证明a,m1,m2,b比
b,m1,m2,a大呢?

a.m1<=m1.a<= a.m2
再将a跟b交换了,
最后再交换成b m1 m2 a 的字符串,发现是一个递增的过程,所以交换a和b只会字典序上升
不会字典序下降。
日常写法中可以通过一个暴力解加贪心去解决这一类问题。
暴力解:
public static String lowestString1(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
TreeSet<String> ans = process(strs);
return ans.size()==0? "": ans.first();
}
//strs中所有字符串的全排列,返回所有可能的结果
public static TreeSet<String> process(String[] strs) {
TreeSet<String> ans = new TreeSet<>();
if (strs.length == 0) {
ans.add("");
return ans;
}
for (int i = 0; i < strs.length; i++) {
//每一个位置都可以作为第一个字符串
String first = strs[i];
//移除当前作为第一个位置的字符串
String[] nexts = removeIndexString(strs, i);
//求出后续串的排序
TreeSet<String> next = process(nexts);
//每一种结果拼接
for (String cur : next) {
ans.add(first + cur);
}
}
return ans;
}
//{"abc","cks","bct"}
// removeIndexString(arr , 1) -> {"abc", "bct"}
public static String[] removeIndexString(String[] strs, int index) {
String[] ans = new String[strs.length - 1];
int ansIndex = 0;
for (int i = 0; i < strs.length; i++) {
if (i != index) {
ans[ansIndex++] = strs[i];
}
}
return ans;
}
贪心解:
public static class MyComparator implements Comparator<String> {
@Override
public int compare(String a, String b) {
return (a + b).compareTo(b + a);
}
}
public static String lowestString2(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
Arrays.sort(strs, new MyComparator());
String res = "";
for (int i = 0; i < strs.length; i++) {
res += strs[i];
}
return res;
}