排序
内部排序:是指在排序期间 元素全部放在内存中的排序。
内部排序算法的性能取决于算法的时间复杂度和空间复杂度。
1. 插入排序
1.1 直接插入排序
-
图解
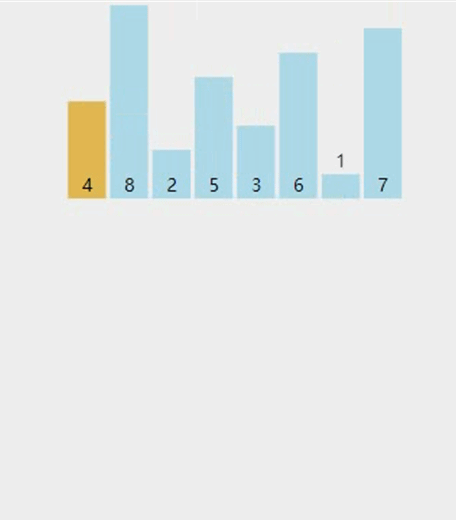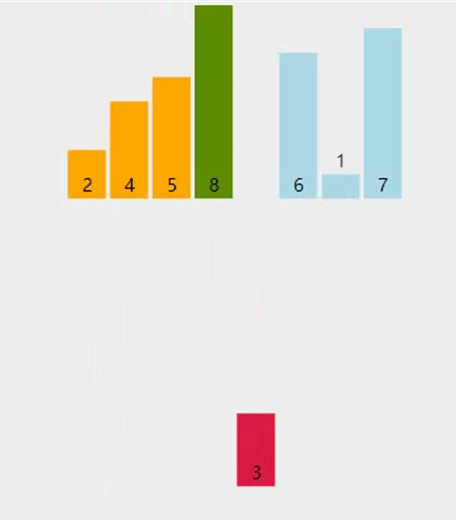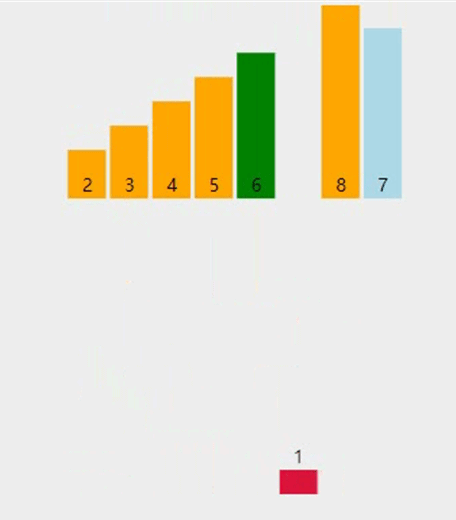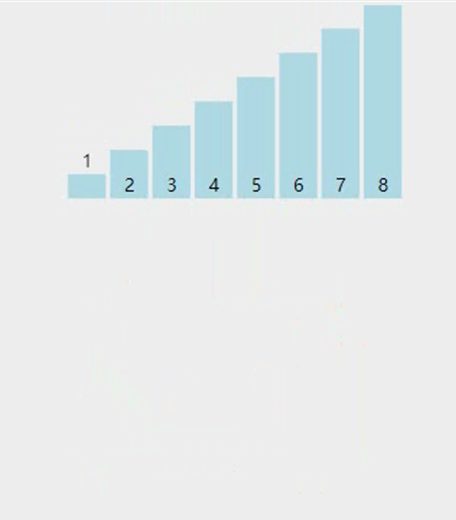
-
基本思想
1. 查找
a[i]元素在第1 ~ i-1中的位置k
2. 将k ~ i-1位置上的所有元素向后移动一个位置
3. 将a[i]复制到a[k]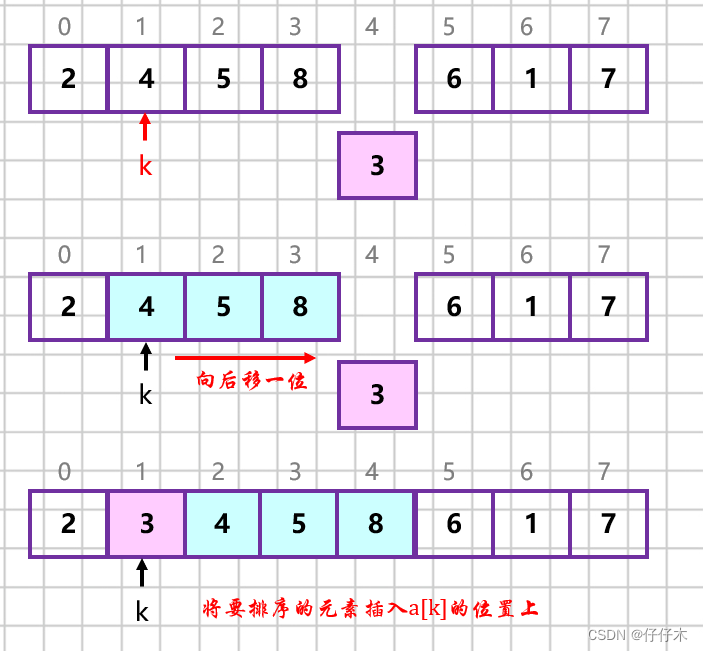
-
代码
方法一:
数组的下标从0开始,如上图。
#include "stdio.h" typedef int ElemType; void Insert(ElemType a[],int n){ ElemType temp; int j; for (int i = 1; i < n; ++i) { //假设a[0]是有序的数组,从a[1]开始进行插入排序 if (a[i]<a[i-1]){ temp=a[i]; for (j = i-1; j >= 0&&a[j]>temp ; --j) //将k ~ i-1位置上的所有元素向后移动一个位置 a[j+1]=a[j]; a[j+1]=temp; } } } int main(){ int n; ElemType a[n]; printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 0; i < n; ++i) { scanf("%d",&a[i]); } Insert(a,n); printf("排序后为:"); for (int i = 0; i < n; ++i) { printf("%d\t",a[i]); } }方法二:
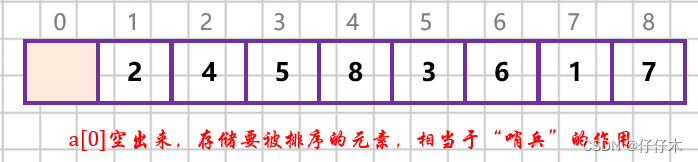
#include "stdio.h" typedef int ElemType; void InsertSort(ElemType a[],int n){ int i,j; for (i = 2; i <=n; i++) { if (a[i]<a[i-1]){ a[0]=a[i]; for (j = i-1; a[0]<a[j]; --j) a[j+1]=a[j]; a[j+1]=a[0]; } } } int main(){ int n; ElemType a[n]; printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 1; i <= n; ++i) { scanf("%d",&a[i]); } InsertSort(a,n); printf("排序后为:"); for (int i = 1; i <= n; ++i) { printf("%d\t",a[i]); } } -
算法性能
空间效率: 仅使用了常数个辅助单元,复杂度为: O ( 1 ) O(1) O(1)
?
时间效率: 平均时间复杂度: O ( n 2 ) O(n^2) O(n2)
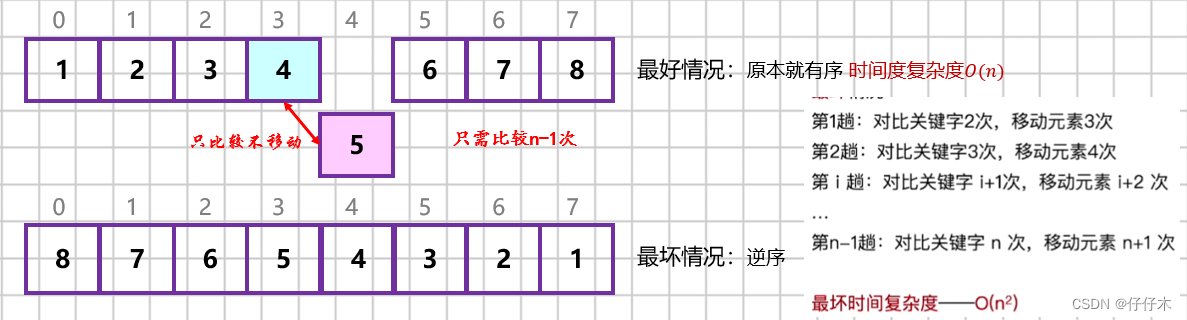
?
稳定性: 由于每次插入元素时总是从后向前先比较在移动,所以不会出现相同元素相对位置发生变化的情况,即直接插入排序是一个稳定的排序方法。
?
适用性: 适用于顺序存储和链式存储的线性表。为链式存储时,可以从前往后查找指定元素的位置。
1.2 折半插入排序
-
图解
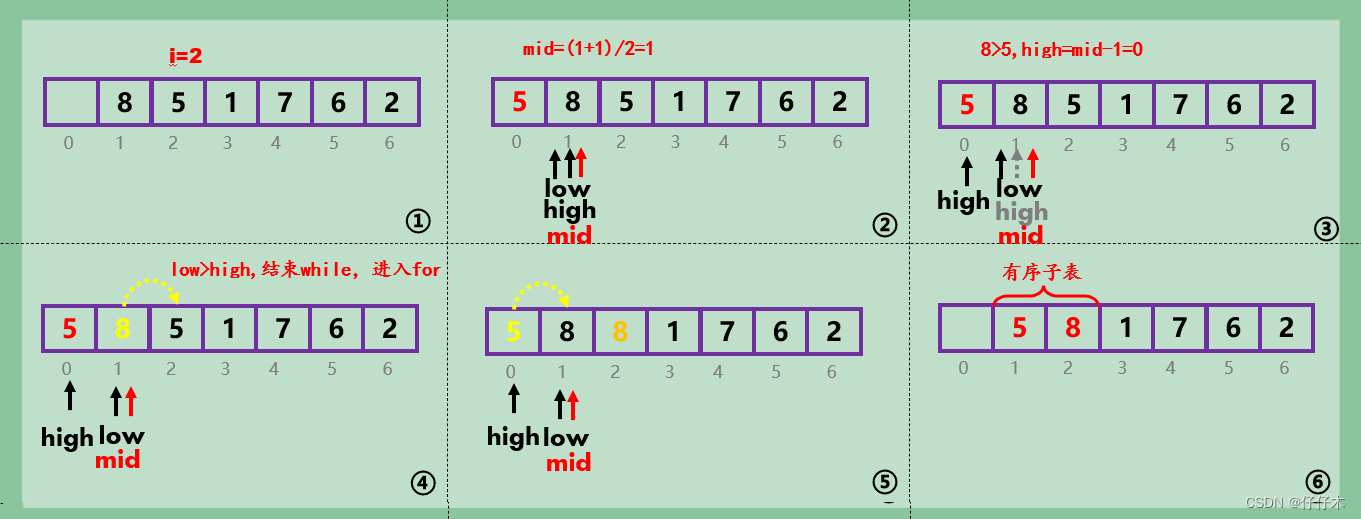
第一趟:
第二趟:
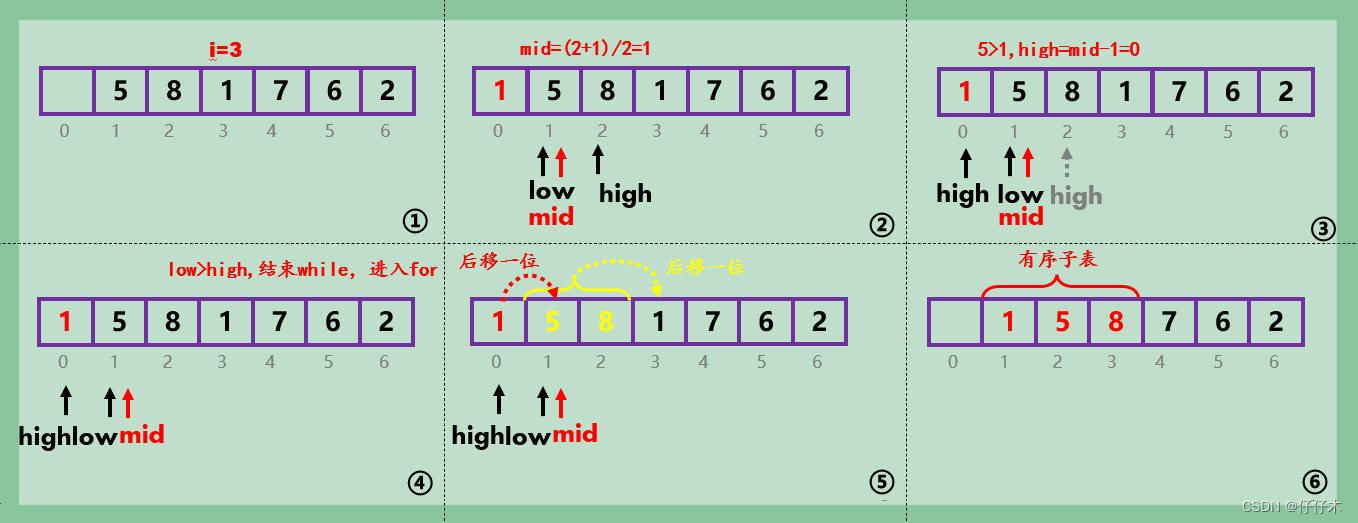
第三趟:
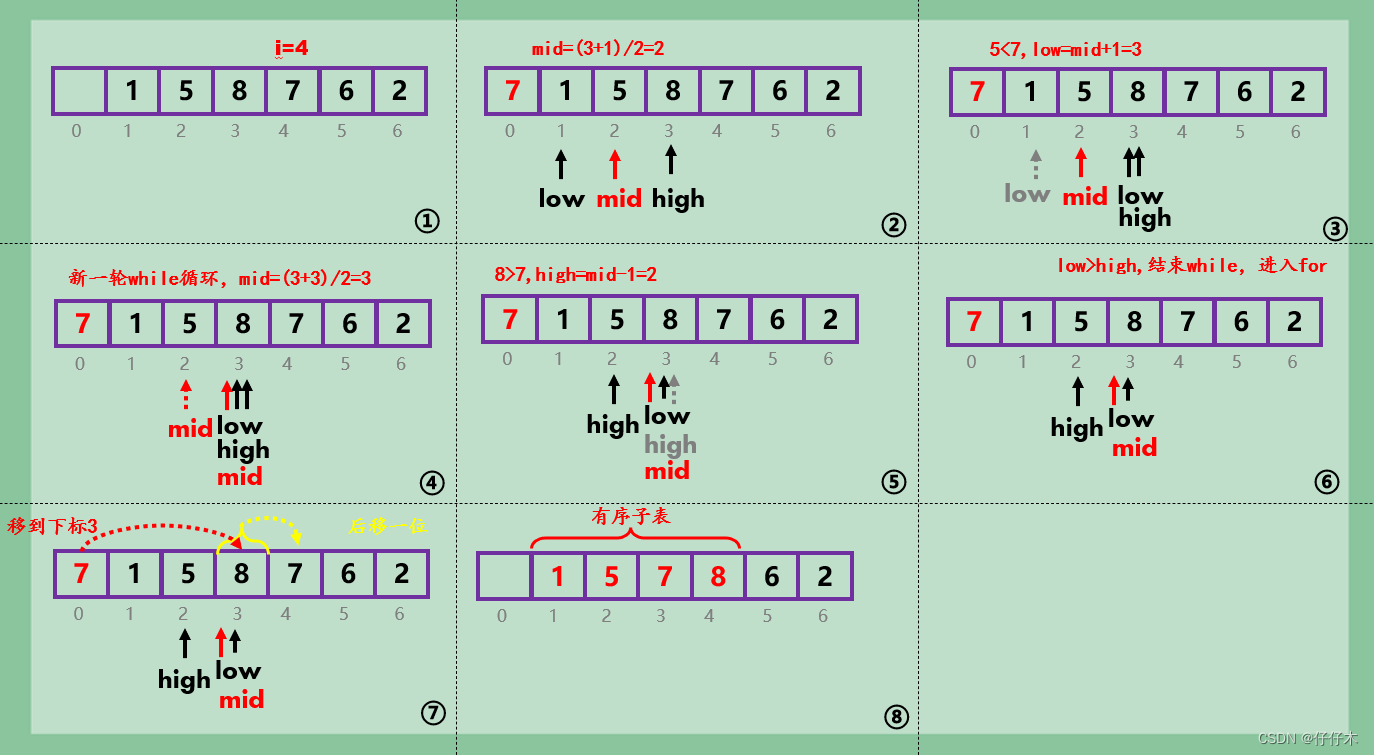
第四趟:略
第五趟:略 -
基本思想
- 与直接插入排序相比较,折半插入排序引入了mid,low,high,减少比较次数。
- 取将有序子表中间值,若a[mid]>a[0] (待排序元素),low=mid+1,反则,high=mid-1;
- 找到比a[0]大的元素,均向后移一位,将a[0]元素插入待排序子表,形成新的子表。
-
代码
#include "stdio.h" typedef int ElemType; void InsertSort(ElemType a[],int n){ int low,hight,mid; for (int i = 2; i <= n; ++i) { a[0]=a[i]; low=1;hight=i-1; while (low<=hight){ mid=(low+hight)/2; if (a[mid]>a[0])hight=mid-1; else low=mid+1; } for (int j = i-1; j >= hight+1 ; --j) a[j+1]=a[j]; a[hight+1]=a[0]; } } int main(){ int n; ElemType a[n]; printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 1; i <= n; ++i) { scanf("%d",&a[i]); } printf("排序后为:"); InsertSort(a,n); for (int i = 1; i <= n; ++i) { printf("%d\t",a[i]); } } -
性能
空间复杂度: O ( 1 ) O(1) O(1)
时间复杂度: O ( n 2 ) O(n^2) O(n2)
稳定性:稳定
适用性:仅适用于顺序表
1.3 希尔排序
-
图解(动图)
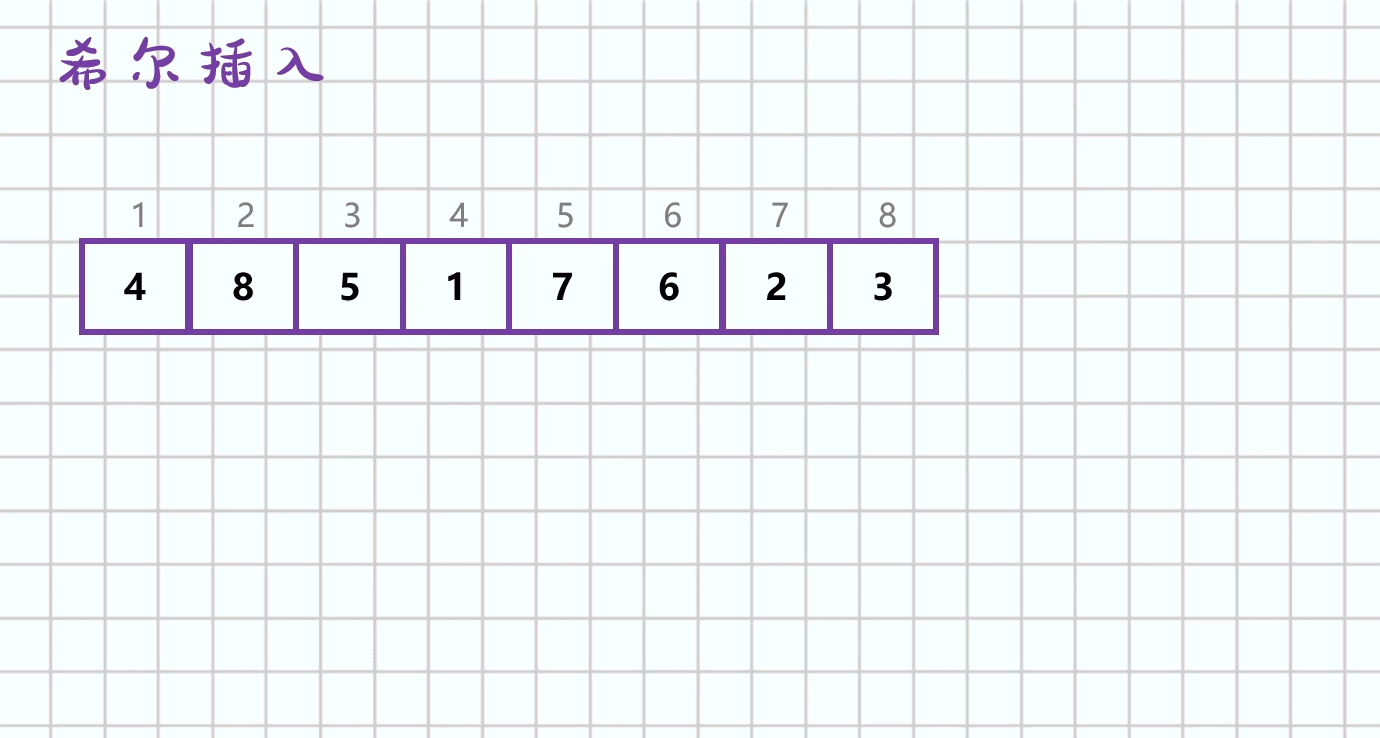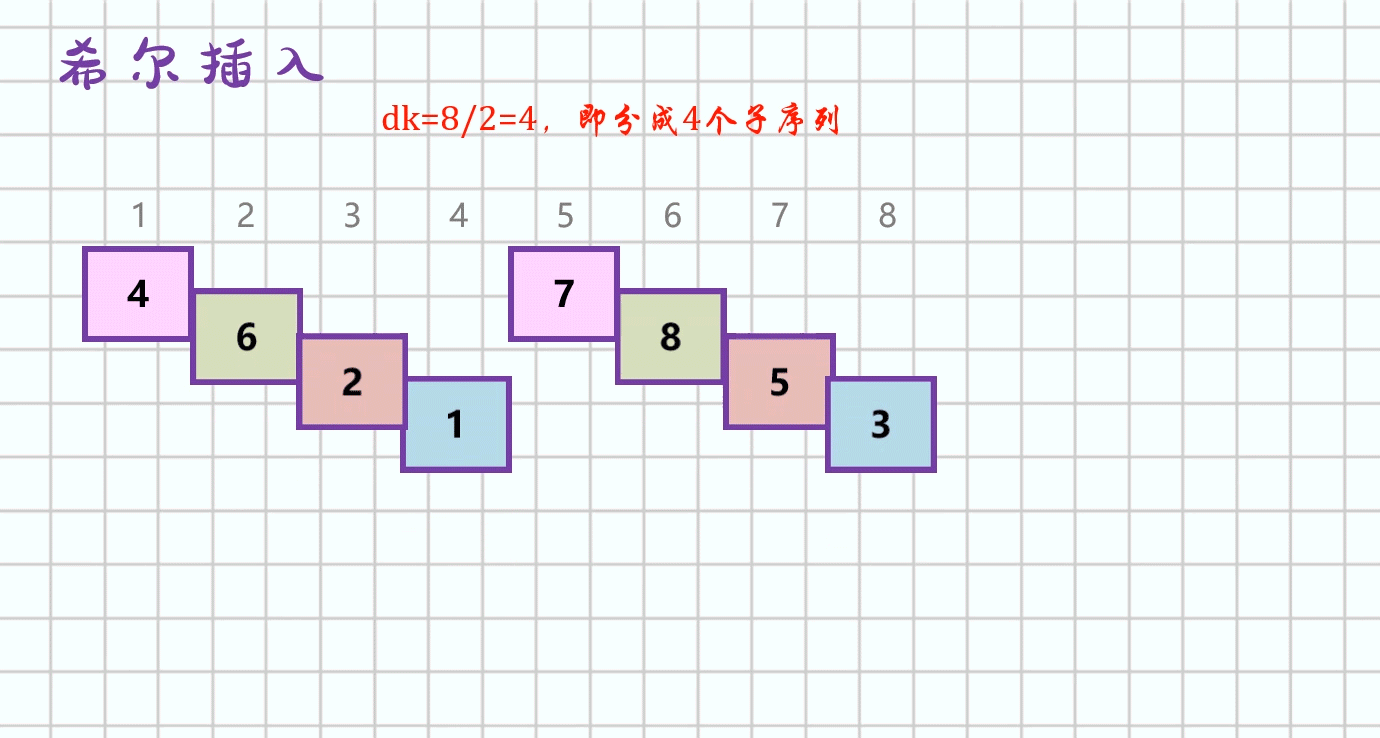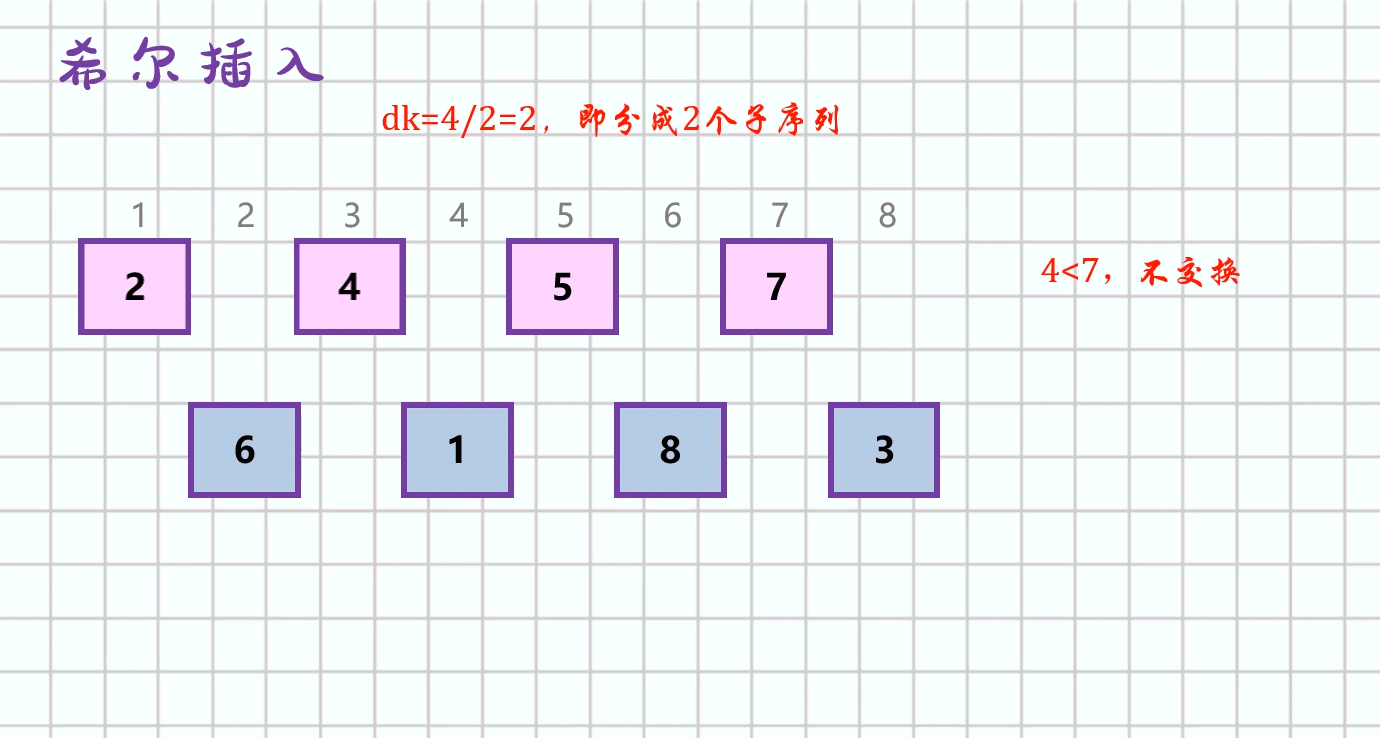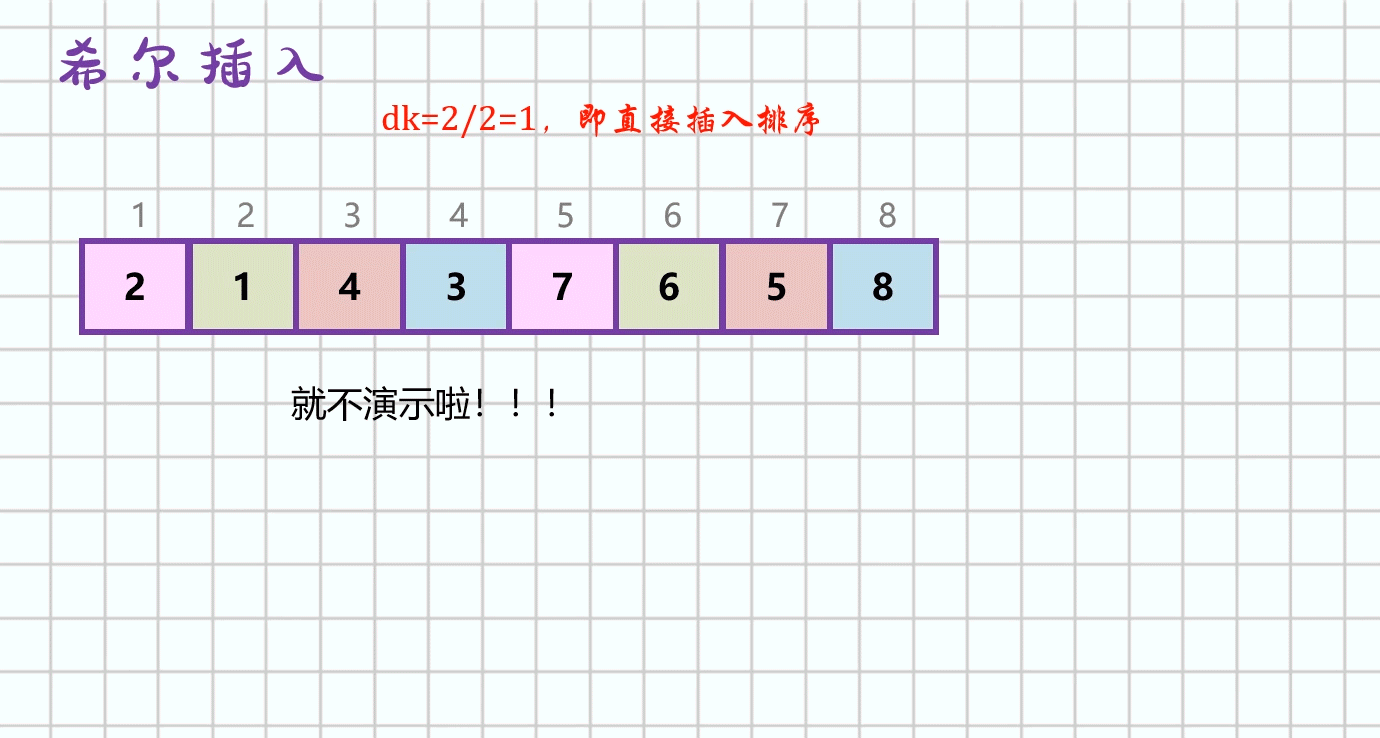
-
基本思想
先将待排序表分割成若千形如
L[i,i+d,i+2d,...,i+kd]的“特殊”子表,即把相隔某个“增量”的记录组成一个子表,对各个子表分别进行直接插入排序,当整个表中的元素已呈“基本有序”时,再对全体记录进行一次直接插入排序。 -
代码
#include "stdio.h" typedef int ElemType; void ShellSort(ElemType a[],int n){ int j; for (int dk = n/2; dk >= 1; dk=dk/2) { //判断每次分成几个序列,只要>=1就排序 for (int i = dk+1; i <= n; ++i) { //dk+1:取到小分队的第二个元素(从第一个元素开始)进行直接插入排序 if (a[i]<a[i-dk]){ a[0]=a[i]; for (j = i-dk; j > 0&&a[0]<a[j]; j-=dk) a[j+dk]=a[j]; a[j+dk]=a[0]; } } } } int main(){ int n; ElemType a[n]; printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 1; i <= n; ++i) { scanf("%d",&a[i]); } printf("排序后为:"); ShellSort(a,n); for (int i = 1; i <= n; ++i) { printf("%d\t",a[i]); } } -
性能
空间效率: 仅使用了常数辅助单位,因而空间复杂度为 O ( 1 ) O(1) O(1)
?
时间效率: 由于希尔排序的时间复杂度依赖于增量序列的函数,这涉及数学上尚未解决的难题,所以其时间复杂度分析比较困难。当n在某个特定范围时,希尔排序的时间复杂度约为 O ( n 1.3 ) O(n^{1.3}) O(n1.3),在最环情况下希尔排序的时间复杂度为 O ( n 2 ) O(n^2) O(n2)
?
稳定性: 当相同关键字的记录被划分到不同的子表时文可能会改变它们之间的相对次序,因此希尔排序是一种不稳定的排序方法。
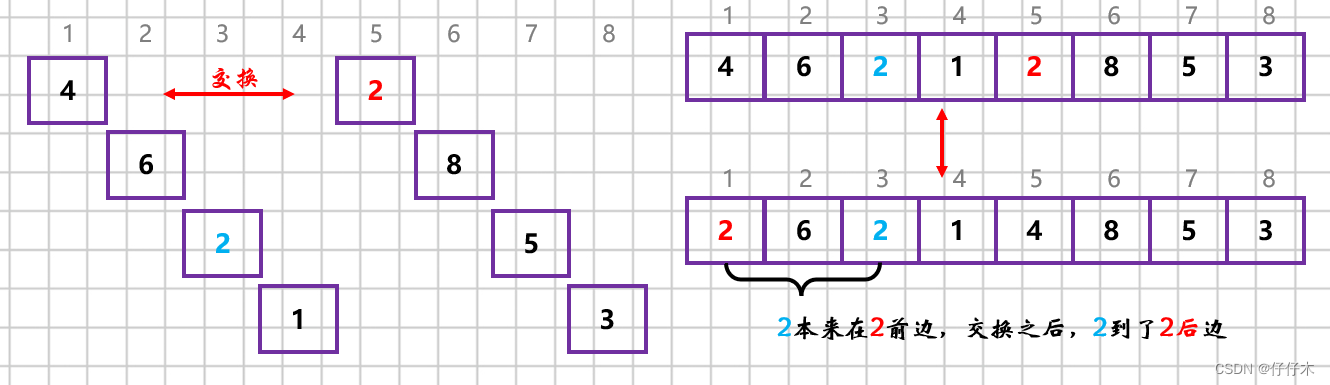
适用性: 希尔排序算法仅适用于线性表为
顺序存储的情况。
2. 交换排序
2.1 冒泡排序
-
图解
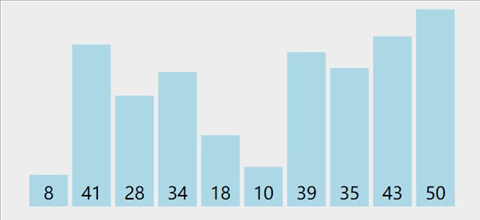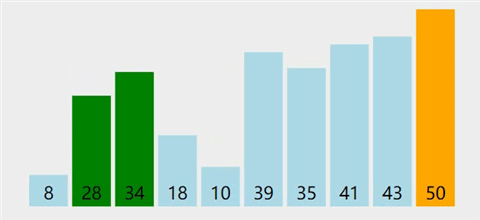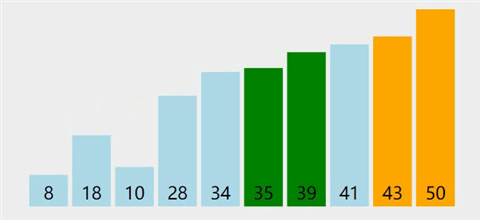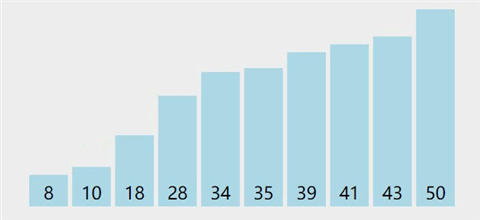
-
基本思想
从后往前(或从前往后)两两比较相邻元素的值,若为逆序(即A[i-1]>A[i]),则交换它们,直到序列比较完。我们称它为第一趟冒泡,结果是将最小的元素交换到待排序列的第一个位置(或将最大的元素交换到待排序列的最后一个位置),关键字最小的元素如气泡一般逐渐往上“漂浮”直至“水面”(或关键字最大的元素如石头一般下沉至水底)。下一趟冒泡时,前一趟确定的最小元素不再参与比较,每趟冒泡的结果是把序列中的最小元素(或最大元素)放到了序列的最终位置……这样最多做n-1趟冒泡就能把所有元素排好序。
-
代码
方法一:将最大元素交换到待排序列的最后一个位置
#include "stdio.h" typedef int ElemType; void BubbleSort(ElemType a[],int n){ bool flag; for (int i = 0; i < n-1; ++i) { flag= false; for (int j = 0; j < n-i-1; ++j) { if (a[j]>a[j+1]){ int temp=a[j]; a[j]=a[j+1]; a[j+1]=temp; flag=true; } } if (!flag) return; } } int main(){ int n; ElemType a[n]; printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 0; i < n; ++i) { scanf("%d",&a[i]); } printf("排序后为:"); BubbleSort(a,n); for (int i = 0; i < n; ++i) { printf("%d\t",a[i]); } }运行截图:

方法二:将最小元素交换到待排序列的第一个位置
#include "stdio.h" typedef int ElemType; void BubbleSort(ElemType a[],int n){ bool flag; for (int i = 0; i < n-1; ++i) { flag= false; for (int j = n-1; j >i; --j) { if (a[j-1]>a[j]){ int temp=a[j]; a[j]=a[j-1]; a[j-1]=temp; flag=true; } } if (!flag) return; } } int main(){ int n; ElemType a[n]; printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 0; i < n; ++i) { scanf("%d",&a[i]); } printf("排序后为:"); BubbleSort(a,n); for (int i = 0; i < n; ++i) { printf("%d\t",a[i]); } }运行截图:

-
性能
空间效率: 仅使用了常数辅助单位,因而空间复杂度为 O ( 1 ) O(1) O(1)
?
时间效率: 最坏情况: O ( n 2 ) O(n^2) O(n2);平均时间复杂度: O ( n 2 ) O(n^2) O(n2);
?
稳定性: 稳定
?
适用性: 适用于线性表为顺序存储和链式存储。
2.2 快速排序
-
图解(动图以后再补)
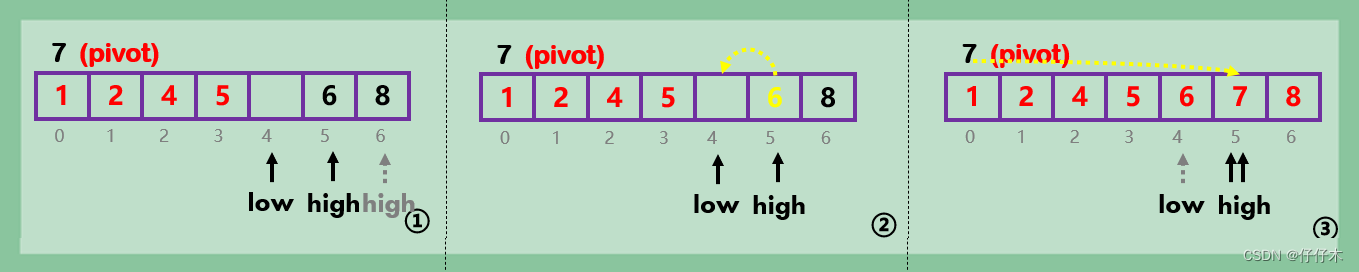
第一趟的排序:
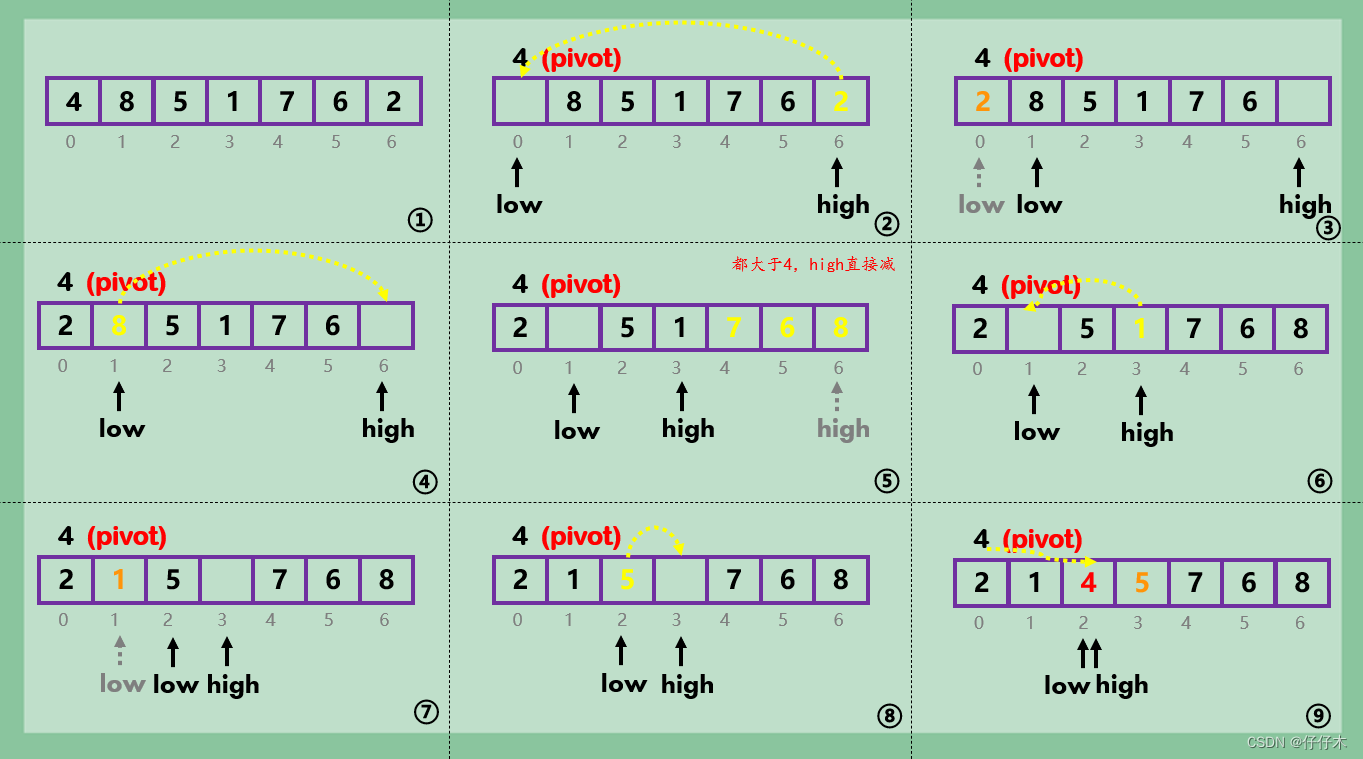
第二趟:

第三趟:
-
基本思想
快速排序的基本思想是基于分治法的:
- 在数组a[0…n-1]中选取pivot:a[0] 作为枢轴(或基准,通常取首元素)
- 通过对比排序,将pivot元素放置在k位置上,a[0…k-1]<pivot<a[k+1…n-1],完成第一趟排序。
- 然后分别递归,将a[0…k-1]、a[k+1…n-1]子表按照1、2步骤排序。直至所有元素排序完成。
-
代码
#include "stdio.h" typedef int ElemType; int Partition(ElemType a[],int low,int high){ ElemType pivot=a[low]; while(low<high){ while (low<high&&a[high]>=pivot)--high; a[low]=a[high]; while (low<high&&a[low]<=pivot) ++low; a[high]=a[low]; } a[low]=pivot; return low; } void QuickSort(ElemType a[],int low,int high){ bool flag; if (low<high){ int pivotpos=Partition(a,low,high); QuickSort(a,low,pivotpos-1); QuickSort(a,pivotpos+1,high); } } int main(){ int n; ElemType a[n]; printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 0; i < n; ++i) { scanf("%d",&a[i]); } printf("排序后为:"); QuickSort(a,0,n-1); for (int i = 0; i < n; ++i) { printf("%d ",a[i]); } } -
性能
时间复杂度和空间复杂度

稳定性:不稳定
3. 选择排序
3.1 简单选择排序
-
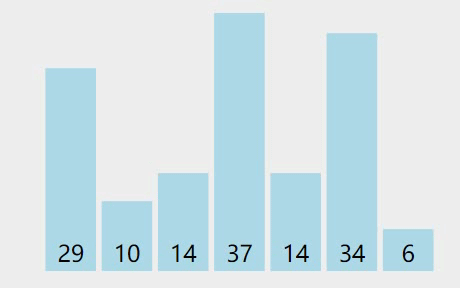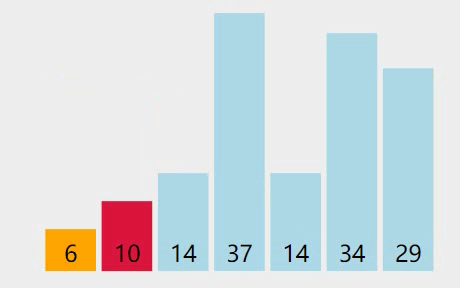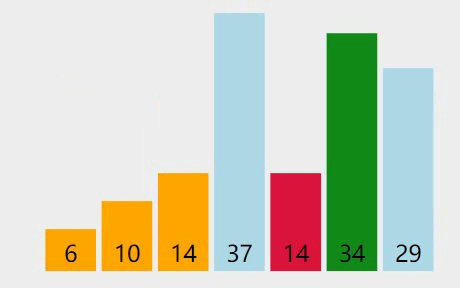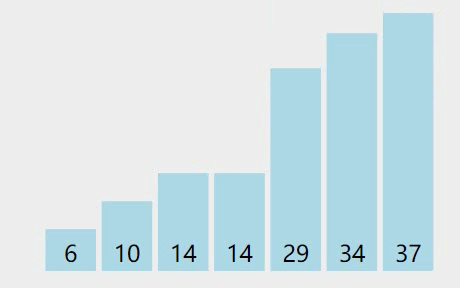
图解
-
基本思想
- 在a[0…n-1]中,将a[0]设为最小元素,设min=0
- 在a[1…n-1]中找到小于a[0]的最小的元素a[k],令min=k;
- 若min=0,则a[0]最小,不用交换;若min!=0,则a[0]和a[k]进行交换,第一趟排序完成。
- 在a[1…n-1]中继续进行排序。
-
代码
#include "stdio.h" typedef int ElemType; void SelectSort(ElemType a[],int n){ for (int i = 0; i < n-1; ++i) { int min=i; for (int j = i+1; j < n; ++j) if (a[j]<a[min]) min=j; if (min!=i){ int temp=a[min]; a[min]=a[i]; a[i]=temp; } } } int main(){ int n; ElemType a[n]; printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 0; i < n; ++i) { scanf("%d",&a[i]); } SelectSort(a,n); printf("排序后为:"); for (int i = 0; i < n; ++i) { printf("%d ",a[i]); } } -
性能
空间复杂度: O ( 1 ) O(1) O(1)
时间复杂度: O ( n 2 ) O(n^2) O(n2)
稳定性: 不稳定使用性:顺序表和链表都适用。
3.2 堆排序
4. 归并排序和基数排序
4.1 归并排序
-
图解
2路归并排序
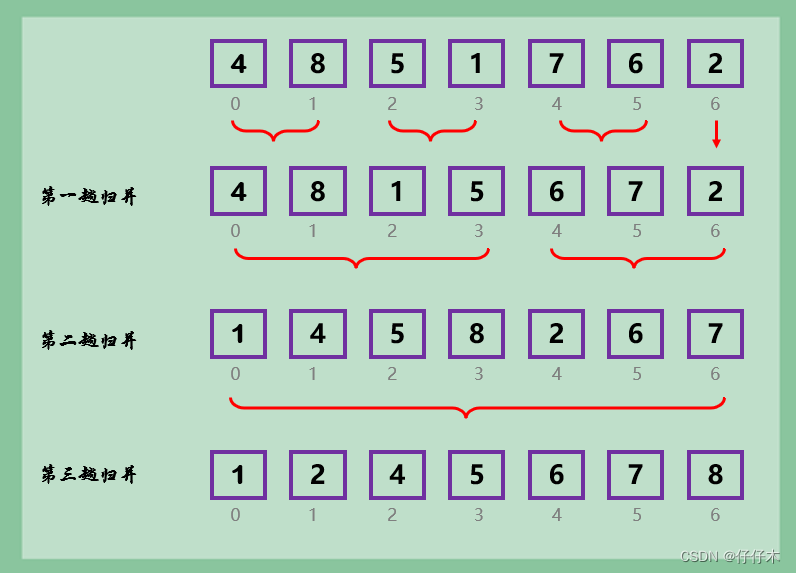
-
基本思想
- 将待排序列分成长度为1的子表,然后两两归并,形成有序子表
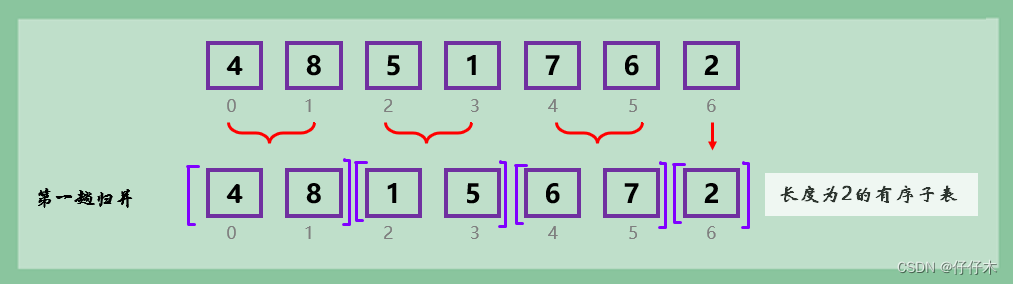
- 然后将子表再次进行归并,直到子表的长度=待排序表的长度。
- 将待排序列分成长度为1的子表,然后两两归并,形成有序子表
-
代码
#include "stdio.h" #include "stdlib.h" typedef int ElemType; ElemType *b; void Merge(ElemType a[],int low,int mid,int high){ int i,j,k; for (int k = low; k <= high; ++k) { b[k]=a[k]; } for (i=low,j=mid+1,k=i; i<=mid&&j<=high; k++) { if (b[i]<=b[j]) a[k]=b[i++]; else a[k]=b[j++]; } while (i<=mid) a[k++]=b[i++]; while (j<=high) a[k++]=b[j++]; } void MergeSort(ElemType a[],int low,int high){ if(low<high){ int mid=(low+high)/2; MergeSort(a,low,mid); MergeSort(a,mid+1,high); Merge(a,low,mid,high); } } int main(){ int n; ElemType a[n]; b=(ElemType*) malloc((n+1)*sizeof (ElemType)); printf("一共有多少个数需要排序:"); scanf("%d",&n); printf("请输入%d个数:",n); for (int i = 0; i < n; ++i) { scanf("%d",&a[i]); } MergeSort(a,0,n-1); printf("排序后为:"); for (int i = 0; i < n; ++i) { printf("%d ",a[i]); } } -
性能
空间效率: O ( n ) O(n) O(n) ???? 创建了一个数组b
时间效率: O ( n l o g k n ) O(nlog_kn) O(nlogk?n)??k指k路归并排序。
稳定性:稳定
4.2 基数排序
-
图解
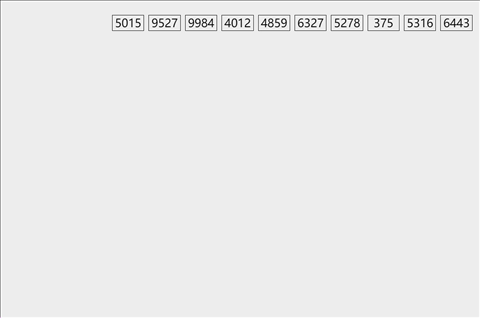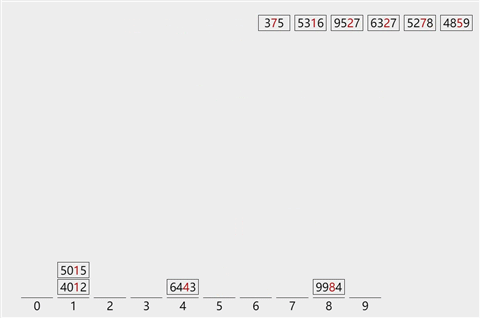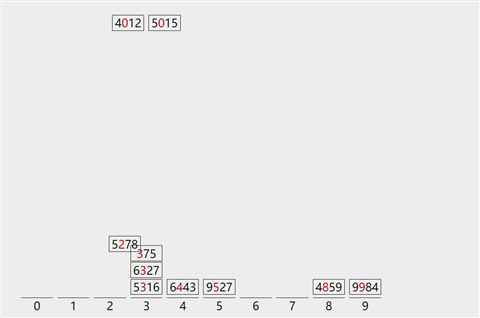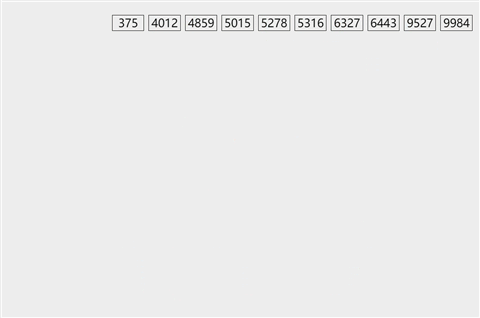
-
基本思想
将各个位数(个位、十位、百位…)进行对比。
为实现多关键字排序,通常有两种方法:第一种是最高位优先(MSD)法,按关键字位权重递减依次逐层划分成若干更小的子序列,最后将所有子序列依次连接成一个有序序列。第二种是最低位优先(LSD)法,按关键字权重递增依次进行排序,最后形成一个有序序列。 -
性能
-
空间复杂度

-
时间复杂度

-
稳定性:稳定
-
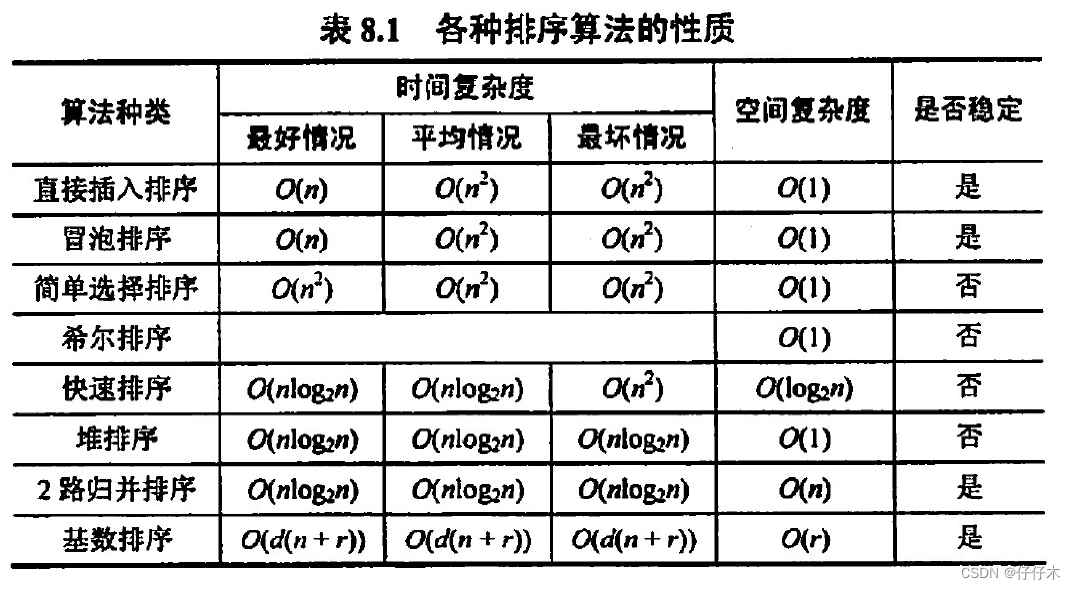
5. 内部排序算法比较及应用
5.1 整体比较
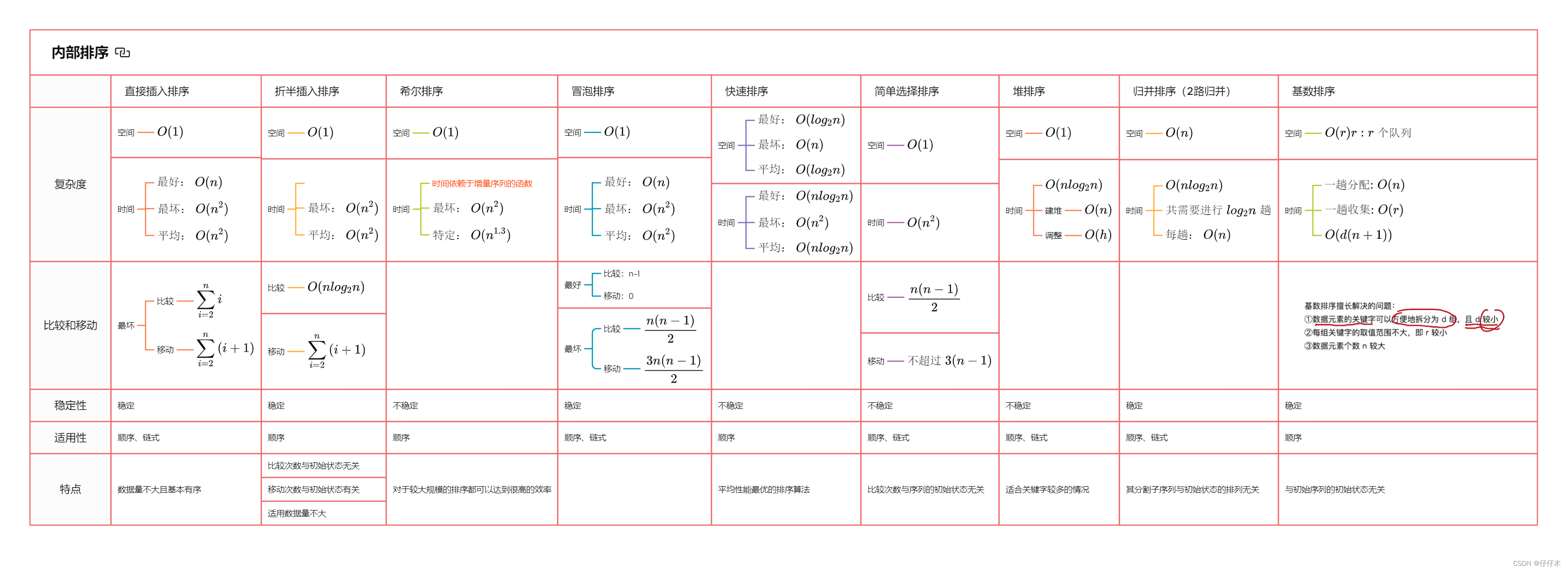
5.2 时间、空间和稳定性
参考资料
《王道:23数据结构考研复习资料》