- 序论:最近在刷到【代码随想录】的博客,看了一下它对题的讲述,讲的很棒,爱刷题的可以看看他对算法和题的叙述,不止在csdn,在微信公众号我好像也看到过,还蛮不错的。
1. 简单叙述一下回溯算法:
首先得说明一下,回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,它实际上就是一个暴力算法,一般加上剪枝的操作进行优化。
我们可以把回溯算法抽象的理解为树型结构,回溯是离不开递归的,我们可以用深度优先搜索(DFS)的算法进行理解(告诉自己撞了南墙要回头,哈哈~),然而我们知道递归是要有终止条件的,所以可以抽象的理解为是一棵高度有限的树。
回溯算法的模板:

(终止条件也就是满足可以存放结果的条件;回溯就是到叶子结点了,像dfs一样(撞了南墙要回头走0.0))?
写题最好是先把树形图先画出来,然后往里面套,需要的话再加上剪枝进行优化。
组合问题
(1).77.组合
题目:

思路:
以一个例子先画树形图理解:(这里画个示例1:n=4,k=2为代表):
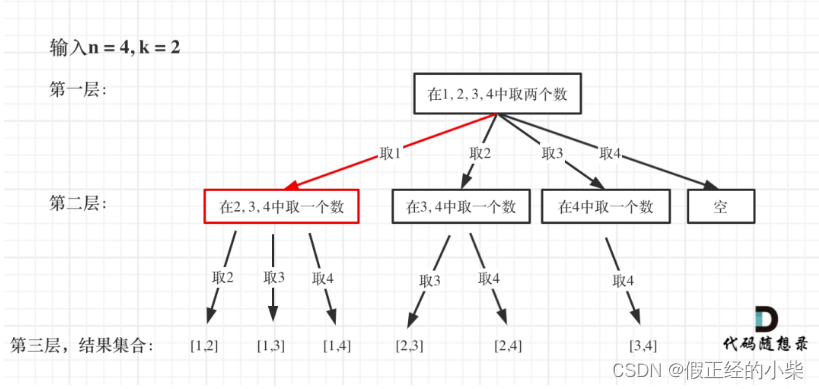
?画完图再进行套模板:我们需要一个容器处理结点vector<int> m//(用来存放元素,然后组成组合),需要另一个容器存放符合要求的组合vector<vector<int>> s//(用来存放组合)
接下来看代码:
#include<bits/stdc++.h>
using namespace std;
class Solution {
private:
vector<int> m;
vector<vector<int>> s;
void huisuo(int startIndex,int n,int k){
if(m.size()==k){
s.push_back(m);
return;
}
for(int i=startIndex;i<=n;++i){
m.push_back(i);
huisuo(i+1,n,k); //这里注意组合要不一样,这里需要以i+1作为参数传递
m.pop_back();
}
}
public:
vector<vector<int>> combine(int n, int k) {
huisuo(1,n,k);
return s;
}
//输出对应的组合
void print(){
for(int i=0;i<s.size();++i){
for(int j=0;j<2;++j){
if(j==0)
cout<<"["<<s[i][j]<<",";
else
cout<<s[i][j]<<"]"<<endl;
}
}
}
};
int main(){
Solution p;
int n, k;
cin>>n>>k;
p.combine(n,k);
p.print();
return 0;
}-----代码可直接拿去测试-----
我们知道不断的递归会导致栈溢出,那么这题是否可以进行优化呢?我们又知道回溯是可以用剪枝进行优化的,那么我们怎么从哪进行剪枝呢?
这个n=4,k=2的例子我们很难看出,换n=4,k=4的例子然后画图:
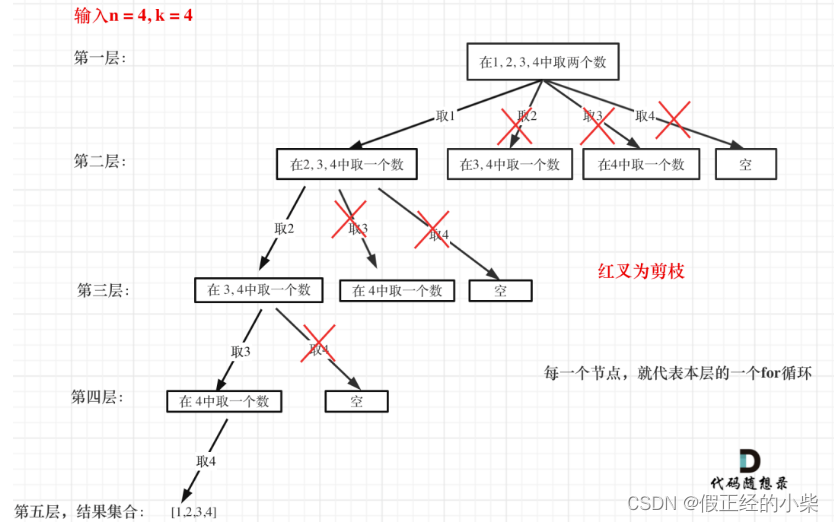
我们知道组合中每个元素都是要不同的,那么当我们知道从startIndex开始到n不够组成组合时,是不是可以进行剪枝呢?那如果够,那我们是不是可以求出至多的那个位置,就是当什么位置上就不能组成组合的前一个,把它当作循环的终止条件元素(相当n)。
如何求这个至多不够形成组合的元素位置呢?
剩多少元素形成新组合的表示形式:k-m.size()
那n-(k-m.size())+1不就表示至多的那个位置。下标是从1开始的,所以需要+1,带上起始位置。
这里剪枝优化就是把上面未优化源码的循环语句改为:
for(int i=startIndex;i<n-(k-m.size())+1;++i)即可;这里就不把全部代码再抄写一遍了。(比较懒,哈哈哈)
(2).39.组合总和
题目:

思路:
按上述思路一样,先以一个示例画出其树形图,然后再模板套(以上面示例1为例吧):
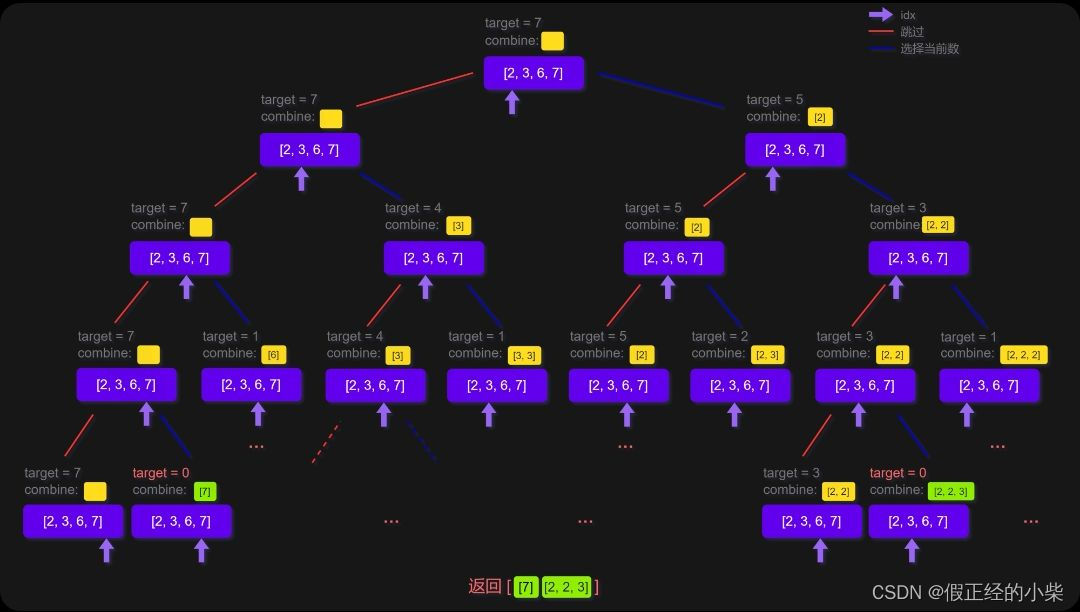
然后再思考怎么处理节点,怎么存放节点?
这里我们可以像上述题一样一个容器处理结点vector<int> m//(用来存放元素,然后组成组合),需要另一个容器存放符合要求的组合vector<vector<int>> s//(用来存放组合)以target是否为0为终止条件。
代码如下:
#include<bits/stdc++.h>
using namespace std;
class Solution {
private:
vector<int> m;
vector<vector<int>> s;
void huisuo(vector<int>& candidates, int target,int startIndex){
if(target==0){
s.push_back(m);
return;
}
for(int i=startIndex;i<candidates.size();++i){
if(target-candidates[i]<0)//这里搞个小剪枝,但这不是最好的剪枝方法哈,为了能测简单的测试点不栈溢出
continue;
m.push_back(candidates[i]);
huisuo(candidates,target-candidates[i],i); //这里注意组合要不一样,这里需要以i+1作为参数传递
m.pop_back();
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
huisuo(candidates,target,0);
return s;
}
//输出对应的组合
void print(){
for(int i=0;i<s.size();++i){
for(int j=0;j<s[i].size();++j){
if(j==0&&j==s[i].size()-1)
cout<<"["<<s[i][j]<<"]"<<endl;
else if(j==0)
cout<<"["<<s[i][j]<<",";
else if(j==s[i].size()-1)
cout<<s[i][j]<<"]"<<endl;
else
cout<<s[i][j]<<",";
}
}
}
};
int main(){
Solution p;
vector<int> nums;
int n;
cin>>n;
for(int i=0;i<n;++i){
int x = 0;
cin>>x;
nums.push_back(x);
}
int target;
cin>>target;
p.combinationSum(nums,target);
p.print();
return 0;
}-----代码可直接拿去测试-----
咱看这代码数据大了就运行不了,那我们怎样巧妙的进行剪枝呢?
我们可以先对candidates对象内元素进行排序,然后当target小于0的时候就终止(这样可以减少很多不必要的递归,也可以减少循环里的集合元素)
改动部分代码如下:
class Solution {
private:
vector<int> m;
vector<vector<int>> s;
void huisuo(vector<int>& candidates, int target,int startIndex){
if(target==0){
s.push_back(m);
return;
}
for(int i=startIndex;i<candidates.size();++i){
if(target-candidates[i]<0)//这里搞个小剪枝,但这不是最好的剪枝方法哈,为了能测简单的测试点不栈溢出
break;
m.push_back(candidates[i]);
huisuo(candidates,target-candidates[i],i); //这里注意组合要不一样,这里需要以i+1作为参数传递
m.pop_back();
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
huisuo(candidates,target,0);
return s;
}
}其实组合问题方法都一样,先画图后思考如何处理结点,然后套模板,最后可以想想如何剪枝进行优化。
后面几道与组合有关的图就不一一讲述了直接给题看代码。(经过了剪枝的)
(3)40.组合总和 ||
题目:

?
class Solution {
private:
vector<vector<int>> s;
vector<int> m;
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
huisuo(candidates,target,s,m,0);
return s;
}
void huisuo(vector<int>& candidates, int target,vector<vector<int>> &s,vector<int> m,int startIndex){
if(target==0){
s.push_back(m);
return;
}
for(int i = startIndex;i<candidates.size();++i){
if(target-candidates[i]<0)
break; if(i>startIndex&&candidates[i]==candidates[i-1])
continue;
m.push_back(candidates[i]);
huisuo(candidates,target-candidates[i],s,m,i+1);
m.pop_back();
}
}
};(4)216.组合总和 |||
题目:

?
class Solution {
private:
vector<vector<int>> s;
vector<int> m;
vector<int> nums;
public:
Solution(){
for(int i=1;i<10;++i)
nums.push_back(i);
}
vector<vector<int>> combinationSum3(int k, int n) {
huisuo(k,n,0);
return s;
}
void huisuo(int k,int n,int startIndex){
if(m.size()==k&&n==0){
s.push_back(m);
return;
}
for(int i=startIndex;i<9;++i){
if(n-nums[i]<0||m.size()==k)
break;
m.push_back(nums[i]);
huisuo(k,n-nums[i],i+1);
m.pop_back();
}
}
};(5)377.组合总和 IV
题目:

?回溯解法:
class Solution {
private:
int count;
void huisuo(vector<int>& nums, int target){
if(target==0){
++count;
return;
}
for(int i=0;i<nums.size();++i){
target -= nums[i];
if(target<0)
break;
huisuo(nums,target);
target += nums[i];
}
}
public:
Solution():count(0){}
int combinationSum4(vector<int>& nums, int target) {
sort(nums.begin(),nums.end());
huisuo(nums,target);
return count;
}
};前面就说了回溯算法解题其实就是一种暴力的枚举,这题即使剪枝了,当target比较大,nums内元素比较小时时间复杂度会很大,而且也很容易导致栈溢出。这时候如果你想提高效率,就可以考虑用其他算法进行解题。
我们试着把这题看成一道走楼梯问题,target表示楼层,nums内的元素可以表示每次爬的楼梯层数,返回的组合数可以等价爬到target楼层最多有几种爬法。看到“最多有几种爬法”这几个关键字,我们可以试着用动态规划。以dp数组表示i的组合总数。
动态规划:
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<int> dp(target+1);
dp[0] = 1;
for(int i=1;i<=target;++i){
for(auto x:nums){
if(x<=i&& dp[i - x] < INT_MAX - dp[i])
dp[i] += dp[i-x];
}
}
return dp[target];
}
};看完下回看见组合问题那不就轻轻松松吗?
点个小赞鼓励一下吧~
?