归并排序实现
归并排序大概思路:
归并时间复杂度:O(n*logn);
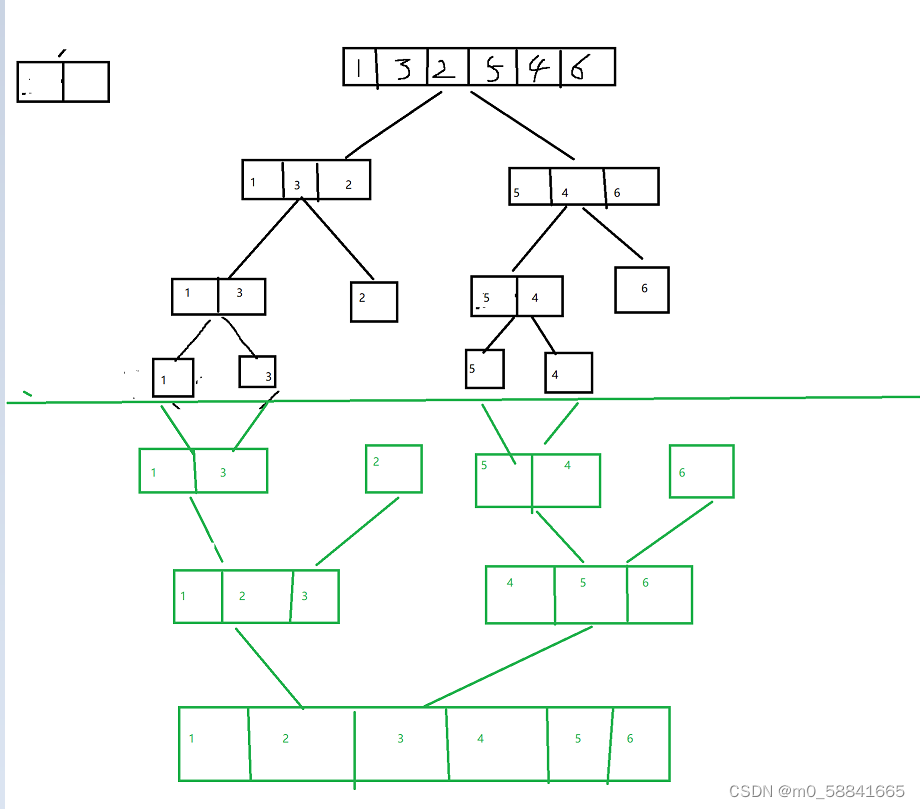
就是把一组数组从中间分成两组;记位左组,和右组;然后再把左右组继续分成新的左组右组,直到左组右组有序(左组和组内分别为都只有一个元素),然后将这两个有序的左右组有序的合成一个数组,就是图片中绿色部分的过程;接下来来结合代码更好的理解下吧 。代码如下:
递归版:
import java.util.Arrays;
public class t {
public static void main(String[] args) {
int[] arr = {1,3,2,5,4,6};
guib(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
public static void guib(int[] arr,int l,int r){ //把数组分成左组和右组
if(l ==r){
return;
}
int m = l+(r-l)/2;
guib(arr,l,m);
guib(arr,m+1,r);
mage(arr,l,r,m);
}
public static void mage(int[] arr,int l,int r,int m){ // 将左右组进行排序
int[] hep = new int[r-l+1];
int p1 = l;
int p2 = m+1;
int i = 0;
while (p1<=m && p2<=r){
if(arr[p1]<=arr[p2]){
hep[i] = arr[p1];
i++;
p1++;
}else {
hep[i] = arr[p2];
i++;
p2++;
}
}
while(p1<=m){
hep[i] = arr[p1];
i++;
p1++;
}
while(p2<=r){
hep[i] = arr[p2];
i++;
p2++;
}
for(int j = 0;j< hep.length;j++){ //将排完的数在放回到原数组
arr[l+j] = hep[j];
}
}
}
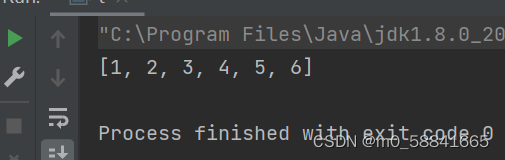
运行结果:
非递归版:
import java.util.Arrays;
public class t {
public static void main(String[] args) {
int[] arr = {1,3,2,5,4,6};
int i = 1;
int l = 0;
int r = 0;
while(i<arr.length){
l = 0;
while (l<arr.length){
int m = l+i-1;
if(m>arr.length-1){
break;
}
r = Math.min(arr.length-1,m+i);
mage(arr,l,r,m);
l =r+1;
}
i = i*2;
}
System.out.println(Arrays.toString(arr));
}
public static void mage(int[] arr,int l,int r,int m){ // 将左右组进行排序
int[] hep = new int[r-l+1];
int p1 = l;
int p2 = m+1;
int i = 0;
while (p1<=m && p2<=r){
if(arr[p1]<=arr[p2]){
hep[i] = arr[p1];
i++;
p1++;
}else {
hep[i] = arr[p2];
i++;
p2++;
}
}
while(p1<=m){
hep[i] = arr[p1];
i++;
p1++;
}
while(p2<=r){
hep[i] = arr[p2];
i++;
p2++;
}
for(int j = 0;j< hep.length;j++){ //将排完的数在放回到原数组
arr[l+j] = hep[j];
}
}
}
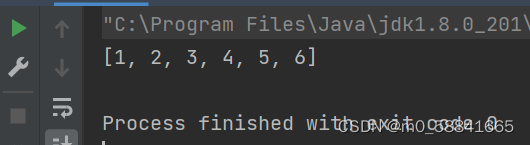
运行结果:
改写归并完成算法题
一.第一种
1.小和问题:假设给定一个数组:arr ;请算出数组中左边小的数加起来的和是多少;
例如:arr = {1,3,2,4};左边比1小的数没有;
左边比3小的数:1;
左边比2小的数:1;
左边比4小的数: 1,2,3;
最后求出它们的和:1+1+1+2+3 =8;
解题代码:
import java.util.Arrays;
public class t {
public static int k;
public static void main(String[] args) {
int[] arr = {1,3,2,4};
int i = 1;
int l = 0;
int r = 0;
pai(arr,0,arr.length-1);
System.out.println(k);
}
public static void pai(int[] arr,int l,int r){
if(l ==r){
return;
}
int m = l+(r-l)/2;
pai(arr,l,m);
pai(arr,m+1,r);
mage(arr,l,r,m);
}
public static void mage(int[] arr,int l,int r,int m){ // 将左右组进行排序
int[] hep = new int[r-l+1];
int p1 = l;
int p2 = m+1;
int i = 0;
while (p1<=m && p2<=r){
if(arr[p1]<arr[p2]){
k = (r-p2+1)*arr[p1]+k;// 这里是用来记录和的
hep[i] = arr[p1];
i++;
p1++;
}else {
hep[i] = arr[p2];
i++;
p2++;
}
}
while(p1<=m){
hep[i] = arr[p1];
i++;
p1++;
}
while(p2<=r){
hep[i] = arr[p2];
i++;
p2++;
}
for(int j = 0;j< hep.length;j++){ //将排完的数在放回到原数组
arr[l+j] = hep[j];
}
}
}
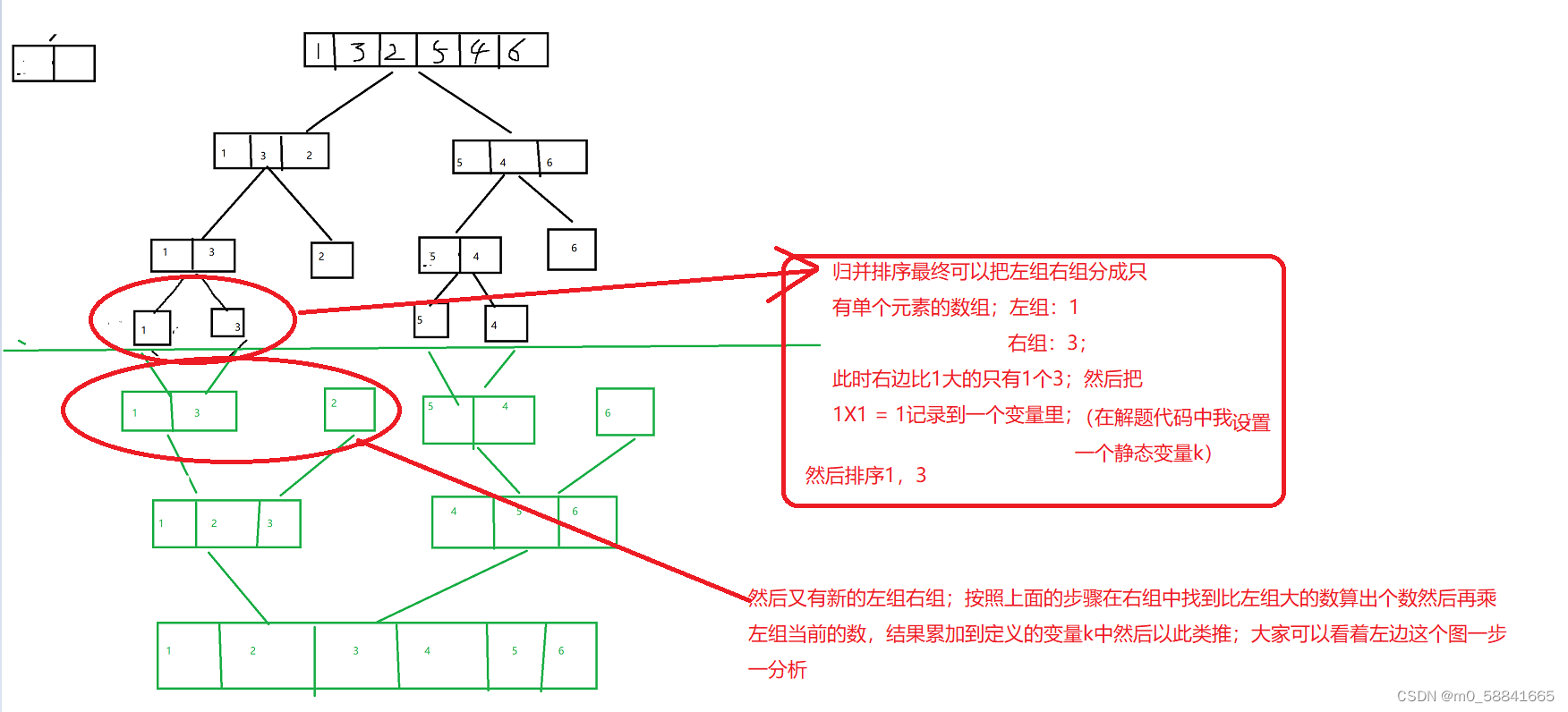
解题思路:题目说的是把数组左边小的数加起来,我们可以转换成找出右边大的数有几个然后用个数乘当前的数字;
例如:arr = {1,3,2,4} ;
右边比1大的数有3个:
右边比3大的数有1个;
右边比2大的数有1个;
右边比4大的数有0个;
所以最后的和就是:1X3+3X1+2X1+4X0 = 8;
这时候就可以用归并排序的改写就能完成了:归并可以把数组分成左组和右组:
举一反三题目一变形
2.同样的我们很容易可以看出第一题的核心就是找出右边大的数;同样我们也可以编程找出右边小的数:
代码如下:
import java.util.Arrays;
public class t {
public static int k;
public static void main(String[] args) {
int[] arr = {3,2,1,2,4,0};
int i = 1;
int l = 0;
int r = 0;
pai(arr,0,arr.length-1);
System.out.println(k);
}
public static void pai(int[] arr,int l,int r){
if(l ==r){
return;
}
int m = l+(r-l)/2;
pai(arr,l,m);
pai(arr,m+1,r);
mage(arr,l,r,m);
}
public static void mage(int[] arr,int l,int r,int m){ // 将左右组进行排序
int[] hep = new int[r-l+1];
int p1 = l;
int p2 = m+1;
int i = 0;
p1 = m;
p2 = r;
while (p1>=l && p2>=m+1){
if(arr[p1]>arr[p2]){
k = k+(p2-m);
p1--;
}else {
p2--;
}
}
p1 = l;
p2 = m+1;
while (p1<=m && p2<=r){
if(arr[p1]<arr[p2]){
//k = (r-p2+1)*arr[p1]+k;
hep[i] = arr[p1];
i++;
p1++;
}else {
hep[i] = arr[p2];
i++;
p2++;
}
}
while(p1<=m){
hep[i] = arr[p1];
i++;
p1++;
}
while(p2<=r){
hep[i] = arr[p2];
i++;
p2++;
}
for(int j = 0;j< hep.length;j++){ //将排完的数在放回到原数组
arr[l+j] = hep[j];
}
}
}
这里k计算的是个数;
题目二
找出数组右边乘2还小的数的个数,例如arr = {1,4,1,2}
在1的右边没有比1小的数
在4的右边有比1小的数1和2,但是1乘2任然小于4;这个1就符合要找的数而2乘2不小于4,所以就不符合要找的数,
解题代码:
import java.util.Arrays;
public class t {
public static int k;
public static int e;
public static int q;
public static void main(String[] args) {
int[] arr = {2,5,9,4};
int i = 1;
int l = 0;
int r = 0;
pai(arr,0,arr.length-1);
System.out.println(q);
}
public static void pai(int[] arr,int l,int r){
if(l ==r){
return;
}
int m = l+(r-l)/2;
pai(arr,l,m);
pai(arr,m+1,r);
mage(arr,l,r,m);
}
public static void mage(int[] arr,int l,int r,int m){ // 将左右组进行排序
int[] hep = new int[r-l+1];
int p1 = l;
int p2 = m+1;
int i = 0;
p1 = m;
p2 = r;
while(p1>=l&&p2>=m+1){
if(arr[p1]<=arr[p2]){
p2--;
}else {
if(arr[p1]>arr[p2]*2){
q = (p2-m)+q;
p1--;
continue;
}
p2--;
}
}
p1 = l;
p2 = m+1;
while (p1<=m && p2<=r){
if(arr[p1]<=arr[p2]){
hep[i] = arr[p1];
i++;
p1++;
}else {
hep[i] = arr[p2];
i++;
p2++;
}
}
while(p1<=m){
hep[i] = arr[p1];
i++;
p1++;
}
while(p2<=r){
hep[i] = arr[p2];
i++;
p2++;
}
for(int j = 0;j< hep.length;j++){ //将排完的数在放回到原数组
arr[l+j] = hep[j];
}
}
}
不难发现在归并排序中我们可以修改一些代码去解决一些算法题;而这种题的特征往往和关键字“左”或者“ 右”有关,因此我们以后做到数组题,题目里有左右关键词可以考虑下归并