209. 长度最小的子数组
一、题目
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
- 1 <= target <= 109
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 105
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/minimum-size-subarray-sum
著作权归领扣网络所有。
二、思路及代码
方法一:前缀和+二分查找(官方题解加上自己一些理解)
下面以nums = [2,3,1,2,4,3]为例子。
(1)先创建一个数组sums,负责记录前缀和,其中sums[i]=sums[i-1]+nums[i-1],如例子中sums = [0,2,5,6,8,12,15]。
(2)遍历sums:在过程中,设置一个target = sums[i-1]+s,然后与sums[i]、sums[i+1]等比较,直到sums[某一个值]大于等于target为止,其目的等价于从对应的nums里第(i-1)这个位置开始遍历求后面数的和,直到大于s为止(这里可以仔细思考思考)。实现这一步是通过lower_bound(sums.begin(), sums.end(), target),功能是在sums数组里找到比target大的值里的最小值。
(3)当不断出现更短长度的时候,及时更新ans。
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int ans = INT_MAX;
if(nums.size() == 0){
return 0;
}
vector<int> sums(nums.size() + 1, 0);
//求出前i-1项和的数组
for(int i = 1; i < sums.size(); i++){
sums[i] = sums[i-1] + nums[i-1];
}
//进行检索
for(int i = 1; i < sums.size(); i++){
int target = s + sums[i-1];//从第i-1位加s,为了和sums后面的元素进行比较,比较过程如下
auto bound = lower_bound(sums.begin(), sums.end(), target);//找到sums中大于target的值里的最小值(注意target是在sums[i-1]基础上加上目标值的,所以可以直接在sums中比较)
if(bound != sums.end()){
//更新ans
ans = min(ans, static_cast<int>((bound - sums.begin()) - (i - 1)));
}
}
return ans==INT_MAX ? 0 : ans;
}
};
方法二:滑动窗口法
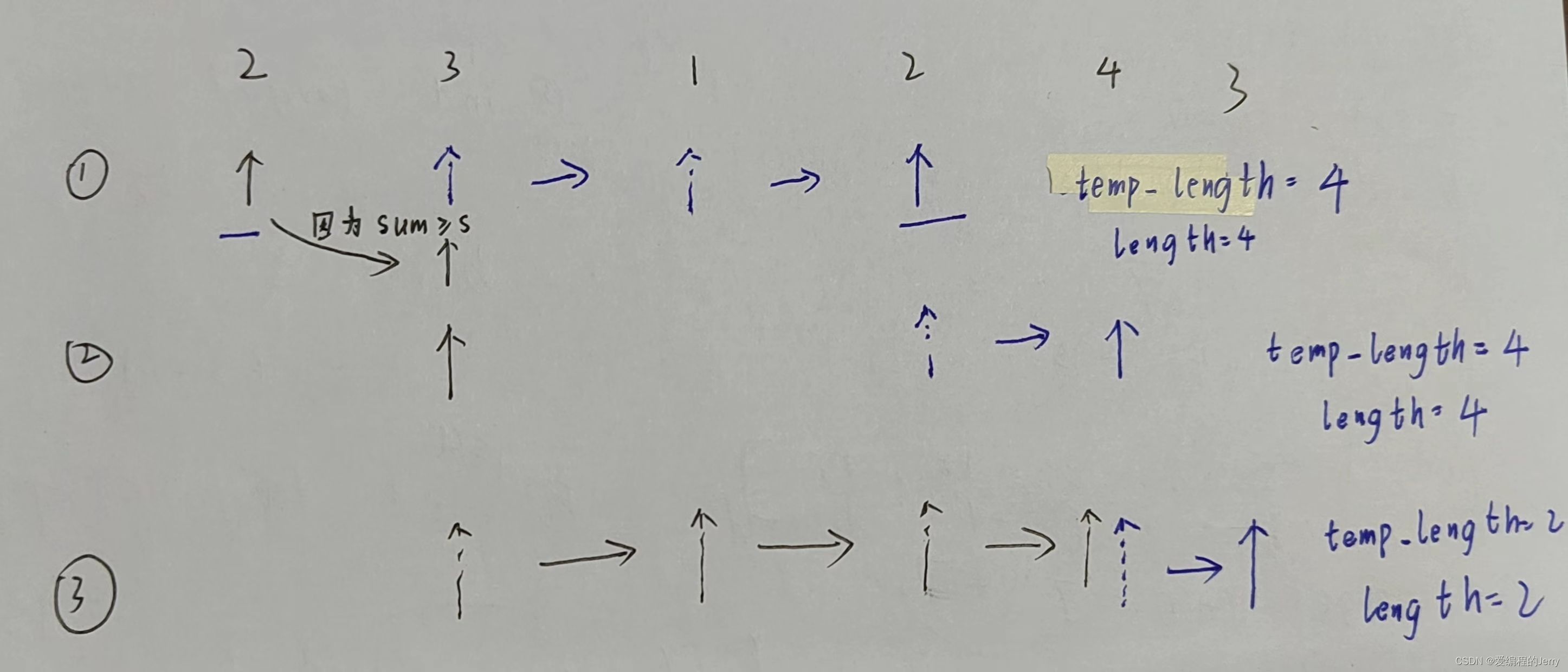
(1)设定左右指针,右指针不断向右遍历,同时求从left到right数组元素的和sum。
(2)当这个和大于等于s时,记录下这时候left到right的长度(temp_length),同时left要向右移动,使得sum继续小于s;而right也一直向右移动。
(3)在循环的过程中,要不断更新长度最小值(length)的值,因为最后返回的是这个length。
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int left = 0;
int sum = 0;
int length = INT_MAX;
int temp_length = 0;
for(int right = 0; right < nums.size(); right++){
sum += nums[right];
while(sum >= s){
temp_length = right - left + 1;//记录temp_length
length = temp_length < length ? temp_length : length;//更新length
sum -= nums[left++];//左边的指针往前移
}
}
return length == INT_MAX ? 0 : length;
}
};