[数据结构与算法]Leetcode1608. 特殊数组的特征值

1.题目描述

给你一个非负整数数组 nums 。如果存在一个数 x ，使得 nums 中恰好有 x 个元素 大于或者等于 x ，那么就称 nums 是一个 特殊数组 ，而 x 是该数组的 特征值 。

注意： x 不必 是 nums 的中的元素。

如果数组 nums 是一个 特殊数组 ，请返回它的特征值 x 。否则，返回 -1 。可以证明的是，如果 nums 是特殊数组，那么其特征值 x 是 唯一的

输入：nums = [3,5]
输出：2
解释：有 2 个元素（3 和 5）大于或等于 2 。

输入：nums = [0,0]
输出：-1
解释：没有满足题目要求的特殊数组，故而也不存在特征值 x 。
如果 x = 0，应该有 0 个元素 >= x，但实际有 2 个。
如果 x = 1，应该有 1 个元素 >= x，但实际有 0 个。
如果 x = 2，应该有 2 个元素 >= x，但实际有 0 个。
x 不能取更大的值，因为 nums 中只有两个元素。

输入：nums = [0,4,3,0,4]
输出：3
解释：有 3 个元素大于或等于 3 。

输入：nums = [3,6,7,7,0]
输出：-1

提示：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 1000

2.思路分析

2.1 模拟

根据题目描述，$x$的取值范围应该是$[1,nums.length]$，那么为了便于判断比对，我们首先需要将nums进行升序排序。然后，根据下图的例子，我们可以得出如下结论：

• 当$x$等于 $nums.length$ 时，需要满足$nums[0]>=nums.length$；
• 当$x$等于 $[1,nums.length?1]$ 时，需要满足$nums[i]>=(res=nums.length?i)$ 并且 $nums[i?1]<res$；
  

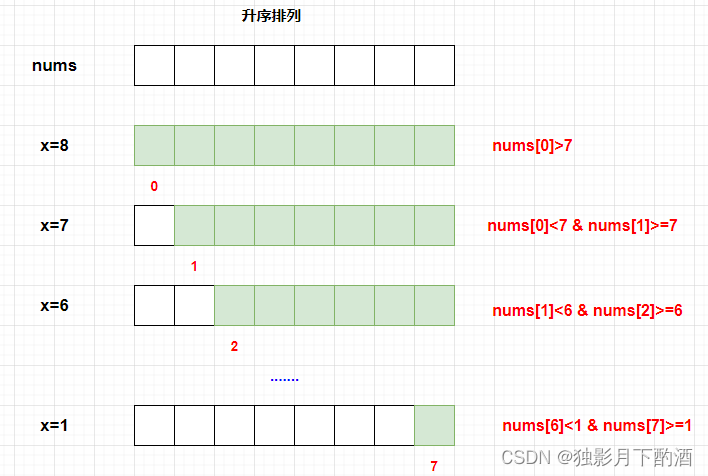
由于特征值x是唯一的，所以，只要有x满足了上面的判断条件，就将x值返回即可。如果没有符合的x，则返回-1；

2.2 二分查找

在 [1, nums.length]之间二分查找，注意：不是找 nums 内元素，只是找从 1 到 nums.length 的数是否满足

• 记当前数为 target
• 如果 target 等于 nums内大于或等于 target 的数量，即满足，则返回 target
• 如果 target 大于 nums 内大于或等于 target 的数量，就是 nums 内没有这么多大于 target 的元素，则收缩右边界
  如果 target 小于 nums 内大于或等于 target 的数量，就是 nums 内太多大于 target 的元素，则收缩左边界

3.代码实现

3.1 模拟

class Solution:
    def specialArray(self, nums: List[int]) -> int:
        # 排序
        nums.sort()
        if nums[0] >= len(nums):
            return len(nums)
        for i in range(1, len(nums)):
            if nums[i] >= len(nums) - i and nums[i - 1] < len(nums) - i:
                return len(nums) - i
        return -1

复杂度分析:

• 时间复杂度：O(nlogn)，其中 n 为数组的长度。
• 空间复杂度：O(logn)，即为排序需要的栈空间。

3.2 二分查找

class Solution:
    def specialArray(self, nums: List[int]) -> int:
        n = len(nums)
        nums.sort()
        left, right = -1, n + 1
        while left <= right:
            mid = (left + right) >> 1
            if (t := n - bisect.bisect_left(nums, mid)) == mid:
                return mid
            elif t < mid:
                right = mid - 1
            else:
                left = mid + 1
        return -1
"""
bisect.bisect_left(a,x,lo=0,hi=len(a),*,key=None)，在有序数组a中[lo,hi]区间内查找x插入的位置，返回的是索引值。如果a中有跟x相同的元素，则x插入的位置是左边，key指定了一个单参数的方法，该方法的返回值作为与k比较的基准。
"""

复杂度分析:

• 时间复杂度：O(nlogn)，其中 n 为数组的长度。
• 空间复杂度：O(logn)，即为排序需要的栈空间。