INDEX
§1 各排序算法的对比
| 稳定性 | 时间复杂度 | 空间复杂度 | ||
|---|---|---|---|---|
| 选择 | ×(交换时可能跨元素交换) | O ( n 2 ) O(n^2 ) O(n2) | O ( 1 ) O(1) O(1) | |
| 冒泡 | √(相等时不交换) | O ( n 2 ) O(n^2 ) O(n2) | O ( 1 ) O(1) O(1) | |
| 插入 | √(相等时不交换) | O ( n 2 ) O(n^2 ) O(n2) | O ( 1 ) O(1) O(1) | |
| 归并 | √(优先归并左侧) | O ( n ? log ? n ) O(n * \log{n}) O(n?logn) | O ( n ) O(n) O(n) | 需要使用稳定性时使用 |
| 快速 | ×(交换时可能跨元素交换) | O ( n ? log ? n ) O(n * \log{n}) O(n?logn) | O ( log ? n ) O(\log{n}) O(logn) | 优先选择,常数项最低 |
| 堆 | ×(交换时可能跨元素交换) | O ( n ? log ? n ) O(n * \log{n}) O(n?logn) | O ( 1 ) O(1) O(1) | 空间限制极大时使用 |
| 计数 | √ | |||
| 基数 | √ |
稳定性
- 所有算法排序后都能符合排序规则
- 但不具有稳定性的排序算不能保证同值元素原始的相对顺序
如 [ … 2(first),…2(sec)…] 排序后变为 […2(sec),2(first)…] - 稳定性对于类型元素没有影响,因为两个 1 没有任何区别,但当元素为对象时可能存在影响
当对对象元素按不同维度进行多次排序时,稳定算法可以继承之前排序的测序,而不稳定的可能将上一轮的顺序洗掉
比如对电商商品进行多维度排序时,需要稳定算法
局限
- 不认为有算法 能做到时间复杂度 < O ( n ? log ? n ) O(n * \log{n}) O(n?logn)
- 不认为有算法能做到时间复杂度 = O ( n ? log ? n ) O(n * \log{n}) O(n?logn),且空间复杂度 < O ( n ) O(n) O(n),且保证稳定性
- 归并可以实现空间复杂度 O ( 1 ) O(1) O(1),使用内部缓存,但实现困难,不如直接用堆
- 归并可以实现空间复杂度 O ( 1 ) O(1) O(1),原地归并,但实现困难,时间复杂度上升为 O ( n ? log ? n ) O(n * \log{n}) O(n?logn),不如直接用插入
- 快速可以实现稳定性,01 stable sort,但实现困难,空间复杂度上升为 O ( n ) O(n) O(n),不如直接用归并
改进或调整(综合排序)
- 一般使用综合排序的思路
即一个算法中基于不同的考虑,按某维度进行划分,分别使用两种算法 - 出于不同时间复杂度优势的考虑
- 按样本量划分,< x 时用
O
(
n
2
)
O(n^2 )
O(n2)算法,反之用
O
(
n
?
log
?
n
)
O(n * \log{n})
O(n?logn) 算法
这是因为算法复杂度是基于 n 很大的总结归纳,但样本较小时受常数项影响可能实际运行时间不符合预期,样本量阈值可以实测后确定 - 大样本时,小时间复杂度算法具有调度优势
- 小样本时,大时间复杂度算法可能有小常数项优势
- 按样本量划分,< x 时用
O
(
n
2
)
O(n^2 )
O(n2)算法,反之用
O
(
n
?
log
?
n
)
O(n * \log{n})
O(n?logn) 算法
- 出于稳定性的考虑
- 按数据类型划分
- 基本类型使用快速排序
- 对象使用归并
§2 基于比较的排序
§2.1 选择排序
执行 n 轮
每轮(i)扫一次剩余数组,记录极值的位置 n,然后交互 i,n 位置的元素
复杂度:
O
(
n
2
)
O(n^2 )
O(n2),
O
(
1
)
O(1)
O(1)
§2.2 冒泡排序
执行 n 轮
每轮扫一次剩余数组,相邻元素按序交互顺序(若正序排列,i > i+1 的元素,交互)
复杂度:
O
(
n
2
)
O(n^2 )
O(n2),
O
(
1
)
O(1)
O(1)
§2.3 插入排序
执行 n 轮
每轮(i)保证前 i 个元素都有序(前 1 个元素有序,然后前 2 个元素有序,然后前 3 个元素有序)
从第 i 个元素往前比,反序就交换
复杂度:
O
(
n
2
)
O(n^2 )
O(n2),
O
(
1
)
O(1)
O(1)
§2.4 归并排序
数组拆分两边,
对左侧排序,对右侧排序,注意前面两个排序也是归并排序,然后归并
归并过程如下:
- 准备辅助数组,与被排序数组等长
- 两个指针指向两个数组 0
- 谁小,将谁写入辅助数组,并移动指针
- 一方写尽后,直接将另一方写进辅助数组
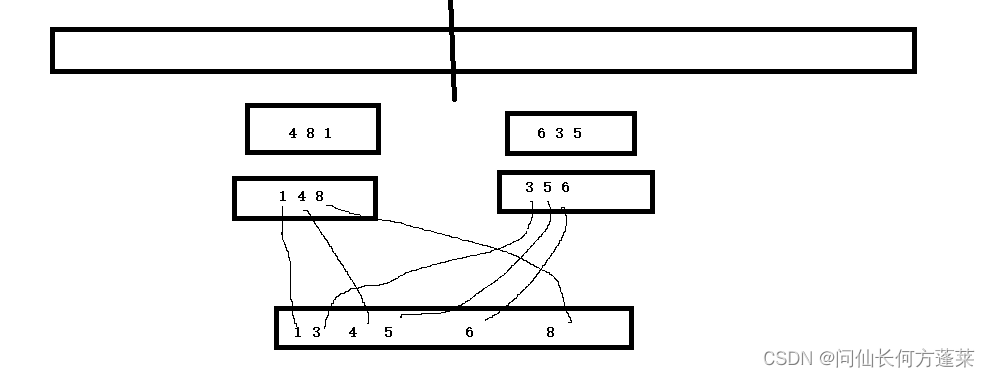
归并的作用:
- 使局部有序
- 因为局部有序,可以通过索引计算统计大于或小于元素的个数
复杂度:
O
(
n
?
log
?
n
)
O(n * \log{n})
O(n?logn),
O
(
n
)
O(n)
O(n)
套用 master :
T
(
n
)
=
2
?
(
n
/
2
)
+
O
(
n
)
T(n) = 2 * (n / 2) + O(n)
T(n)=2?(n/2)+O(n)
§2.5 快速排序
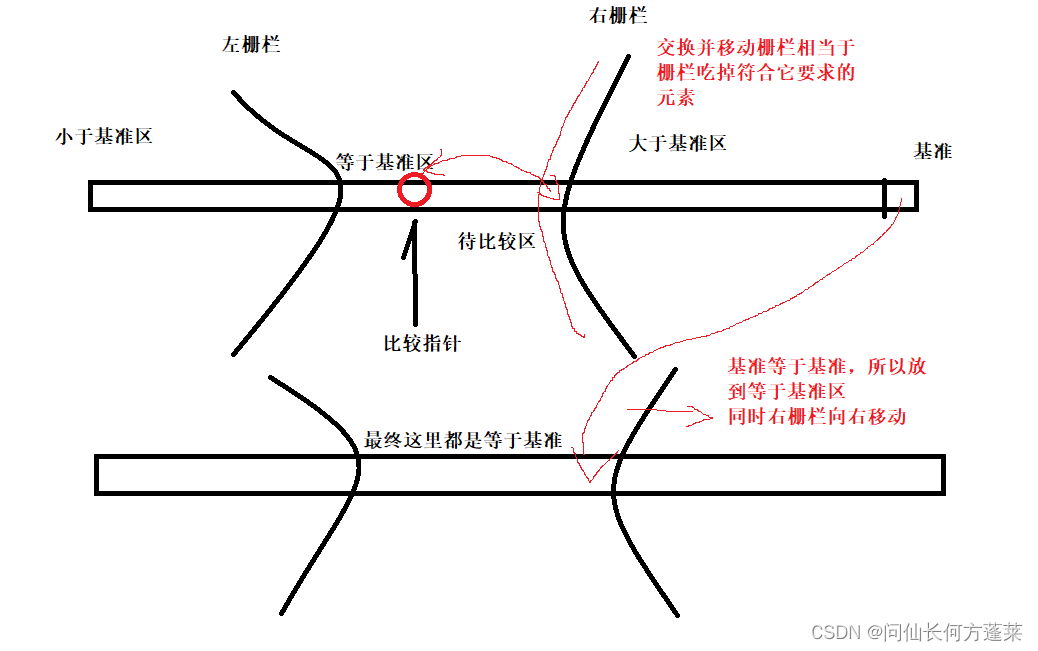
整个过程如下
- partition,即随意选一个数做基准,此数与最右侧交互
- 首尾设置栅栏,一开始在数组外,设置指针指向第一个元素
- 元素与基准比较:
- 小于,和首栅栏的下一个数交互,首栅栏右扩,指针右移
- 大约,和尾栅栏的前一个数交互,尾栅栏左扩,指针不动(因为此时指针指向的是刚刚交换过来的数)
- 等于,什么都不做,指针右移
- 直到指针遇到右栅栏,或左右栅栏接触
- 比较一轮后,尾元素与右栅栏第一个元素交换,右栅栏右扩
- 分别对左右栅栏中的元素重复上述过程
复杂度:
O
(
n
?
log
?
n
)
O(n * \log{n})
O(n?logn),
O
(
log
?
n
)
O(\log{n})
O(logn)
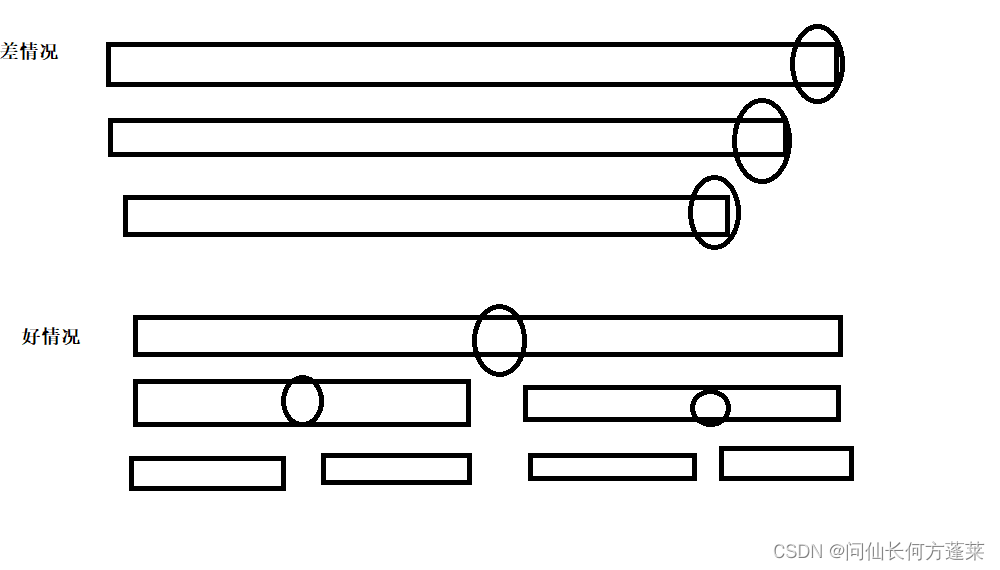
因为是随机取数,存在概率
若直接取最右元素,则可能存在最差情况,此时复杂度为
O
(
n
2
)
O(n^2)
O(n2),
O
(
n
)
O(n)
O(n)
快速排序算法每一层递归时,只有几个指针,所以单层是
O
(
1
)
O(1)
O(1)
- 当最差情况时,基准值的实际排序位置偏右,相当于有几个位置就是几层,因此是 O ( n ) O(n) O(n)
- 当最好情况时,基准值的实际排序位置趋于居中,相当于类似二叉树的展开,因此是
O
(
log
?
n
)
O(\log{n})
O(logn)
§2.6 堆排序
堆排序是使用堆的特性进行排序
整个过程如下,以大顶堆为例
- 将数组整理成堆
若数组没有完全提供,则:
令 heapsize = 0,指针 p 指向数组 0 号元素
指针右移,对指针元素进行 heap insert,heapsize++,重复操作直到整个数组变为堆 - 交互数组 0 和 最大索引元素(即,交互堆顶和堆最后一个元素),因此此时数组 0 即堆顶最大
- heapsize - -
- 对堆顶进行 heapify
- 重复 2 - 4,直到 heapsize == 0
复杂度: O ( n ? log ? n ) O(n * \log{n}) O(n?logn), O ( 1 ) O(1) O(1)
§3 基于数据状况的排序(统计排序)
§3.1 计数排序
统计公司所有年龄的员工的个数,如 [20,50,10,60,30,60…]
准备年龄表,索引表示年龄,值表示统计个数即可
但若是其他统计,统计表可能很大,所以不适用,比如 基数排序
§3.2 基数排序
基于桶
以 10 进制举例 [11,32,36,28,59,100,67]
- 准备 10 个队列,作为桶,每个桶是一个队列
- 依次解析每个数的个位,将它们放到对应桶里
- 按照桶从左到右,桶中元素先进先出的原则整理数组
得到 [100,11,32,36,67,28,59] - 依次解析每个数的十位,将它们放到对应桶里,然后出桶
得到 [100,11,28,32,36,59,67] - 依次解析每个数的百位,将它们放到对应桶里,然后出桶
得到 [11,28,32,36,59,67,100]
常规对数值的排序先参考最高位,因为最高位权重最大,然后参考权重的下一位,以此类推
但这是基于分段排序的,即在对权重稍低的位进行排序时,只能在其权重稍高的位一致的基础上进行,否则相当于打乱了上一轮排序
而基数排序则是将这个过程反过来,通过一轮进桶出桶保证低位的有序性
这使得在下一轮权重稍高的位排序时,同一个桶的元素一定是按权重稍低的位的顺序排布的
这使得即使再整体范围,下一轮排序也不会消除上一轮排序的作用
复杂度: O ( n ? log ? w e i g h t n ) O(n * \log_{weight}{n}) O(n?logweight?n), O ( n ) O(n) O(n)
基于词序表
可以将桶改为词序表
以 10 进制举例 [11,32,36,28,59,100,67]
- 准备一个数组作为 词频表,长度 = 每一位上权重
[1,1,1,0,0,0,1,1,1,1] - 依次解析每个数的个位,将它们统计进 词频表
[1,2,3,3,3,3,4,5,6,7] - 词频表 改为 词序表 a,a[i] = a[i] + a[i-1]
- 按 词序表 规则整理元素,将个位为 i 的元素,放到词序表对应索引的值 -1 的索引上
如上例,元素 36 对应 a[6] = 4,应该放到 index = 4-1 的位置上 - 重复上述过程直到完成最高位
复杂度:
O
(
n
?
log
?
w
e
i
g
h
t
n
)
O(n * \log_{weight}{n})
O(n?logweight?n),
O
(
n
)
O(n)
O(n)
词序表空间复杂度为
O
(
log
?
n
)
O(\log{n})
O(logn),但整理数组时需要一个与原数组等大小的区域,所以是
O
(
n
)
O(n)
O(n)