????????该算法采用重复遍历数组并依次比较相邻元素的方法来排序。由于在冒泡算法进行排序的过程中,最大数/最小数会慢慢“浮”到数组的末尾,所以算法由此命名。
????????冒泡排序的平均时间复杂度是O(),最好情况下的时间复杂度是O(n),最坏情况下的时间复杂度是O(
)。空间复杂度是O(1)。冒泡排序算法是一个稳定的排序算法。
????????冒泡排序的过程同样可以用图说明。我们的目标还是把无序数组以从小到大的顺序排列。
????????首先,我们从第一个数开始遍历,将第一个数与它后面的元素进行对比,发现后面的元素比它小。

?这时,我们需交换这两个元素的值,

?接下来遍历到的是第二个元素。此时第二个元素的值已经变为5。把它和它后方的元素6对比,发现5和6的排列顺序已经是正确的(前面的数小于后面的数),这时候不用交换这两个元素的值,直接继续遍历。

?遍历到第三个元素时,发现它比后面的元素更大,这时,继续交换这两个元素的值。

?在类似的一系列操作后,数组中的最大值被交换到了数组中的最后一个(第8个)位置上。

?我们可以确定末尾元素的值是正确的,所以接下来我们只需要对第1~7个位置上的元素再进行遍历。

?在对第1~7个位置上的元素进行遍历之后,我们可以确定排在第7位的数。同理,在对第1~6个位置上的元素、第1~5个位置上的元素等进行遍历后,我们可以确定数组中排在第6位、第5位的数等。冒泡排序的剩下过程如图
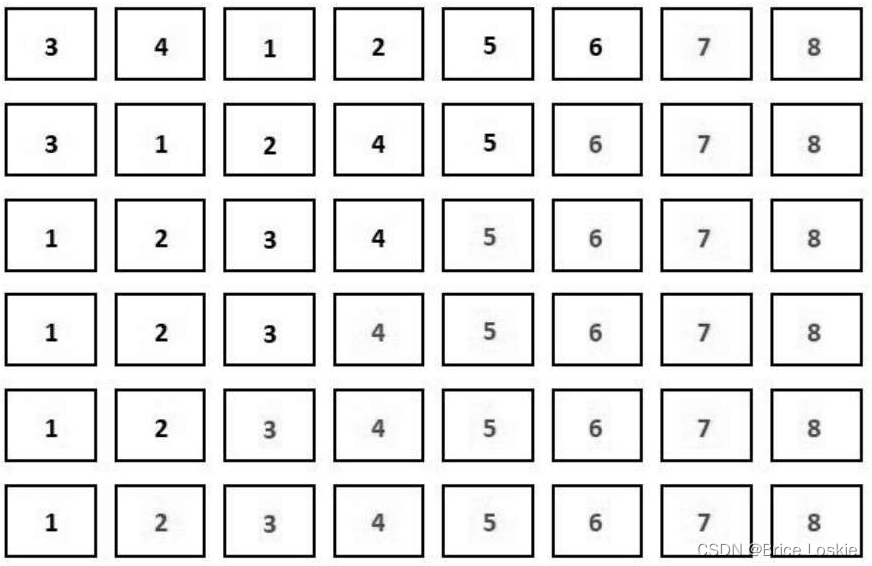
?但是,我们发现,在排好第5个数之后,整个数组的排序就已经完成了,在接下来的遍历中不会再产生元素的交换。这时,我们可以直接结束遍历。
了解了冒泡排序的流程之后,我们再来看看冒泡排序的代码。
nums = [5,3,6,4,1,2,8,7]
for i in range(len(nums),0,-1):
flag =0
for j in range(i-1):
if nums[j]>nums[j+1]:
nums[j],nums[j+1]=nums[j+1],nums[j]
flag=1
pass
pass
if not flag:
break
pass
pass
print(nums)