一、算法原理
选择排序属于不稳定排序法,是一种常用的排序算法,其时间复杂度为O(n^2)。
所谓的不稳定排序算法是指在一组数据中存在多个相同的数据,但是在排序之后,相同数据的前后位置会发生改变。例如有数据{5, 5., 2},使用选择排序法,排序结果为{2, 5., 5},即两个相同数据5的前后位置发生了改变。
选择排序算法原理就是首先固定一个位置i,用该位置上的元素data与后面的元素data_j依次比较大小。以从小到大排序为例,如果data > data_j,则交换这两个数据,直到位置i之后的所有元素都小于该位置上的元素结束。之后执行i++即可完成该数组的排序。
Demo:假设有数据如下表所示:数组名记为data

Step 1:固定下标i为1,取出其位置上的元素data[1],与之后的每一个位置上的元素进行比较,当比较到位置3的时候,该位置上的元素data[3]<data[1],此时交换data[1]和data[3],得到如下数组。

然后从data[4]开始继续和data[1]比较,重复前述工作,最终完成与data[1]的比较,并得到如下的数组:

Step 2:固定下标为2,从data[3]开始比较与data[2]的大小,遇到反序的元素则交换。最终得到如下数组:

Step 3:固定下标为3,从data[4]开始比较与data[3]的大小,遇到反序的元素则交换。最终得到如下数组:

Step 4:固定下标为4,从data[5]开始比较与data[4]的大小,遇到反序的元素则交换。最终得到如下数组:

Step 5:固定下标为5,从data[6]开始比较与data[5]的大小,遇到反序的元素则交换。最终得到如下数组:

二、算法
1. 固定某个位置i的排序算法:
Step 1: 取出元素data[i];
Step 2:j = i+1,比较data[i]和data[j],如果反序则交换data[i]和data[j]的值,转Step 3;
Step 3:j = j+1,如果j等于数组的长度n,则结束,否则转Step 2.
2.选择排序算法:
固定的位置i从1开始直到i=n-1,依次执行上述固定位置的排序算法即可。
从算法流程可以看出,选择排序算法的时间复杂度是O(n^2)。
3.选择排序算法流程图:
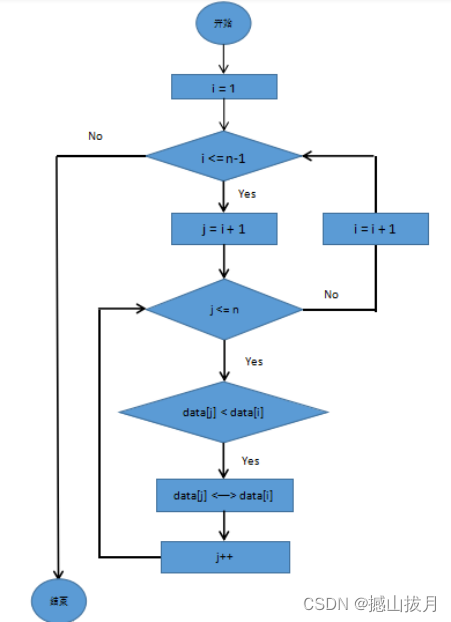
三、算法之C程序
1.选择排序算法之C语言版
/*
功能:使用选择排序法对数组data进行排序
输入参数:
data,已知数据散乱的数组
n,元素的个数
输出参数:
Data,排好序的数组
返回值:无
*/
void SelectionSort( int data[], int n )
{
int i, j, t, k;
for( i = 1; i <= n-1; i++ )
{
//输出每一轮排序前的状态
for( k = 1; k <= n; k++ )
{
printf( "%5d", data[k] );
}
printf( "\n" );
//排序
for( j = i+1; j <= n; j++ )
{
if( data[j] < data[i] )
{
t = data[i];
data[i] = data[j];
data[j] = t;
}
}
}
}
2.完整的代码(仅供参考)
#include"stdio.h"
#define MaxLength 100
void InputData( int &count, int arrt[] );
void SelectionSort( int data[], int n );
int main()
{
int count = 0, i, j;
int data[MaxLength];
InputData( count, data );
SelectionSort( data, count );
for( i = 1; i <= count; i++ )
{
printf( "%5d", data[i] );
}
return 0;
}
/*
功能:使用选择排序法对数组data进行排序,为了显示每一趟排序,增加了输出
输入参数:
data[],已知数据散乱的数组
n,元素的个数
输出参数:
data[],排好序的数组
返回值:无
*/
void SelectionSort( int data[], int n )
{
int i, j, t;
for( i = 1; i <= n-1; i++ )
{
//输出每一趟排序前的数组
for( k = 1; k <= n; k++ )
{
printf( "%5d", data[k] );
}
printf( "\n" );
//排序
for( j = i+1; j <= n; j++ )
{
if( data[j] < data[i] )
{
t = data[i];
data[i] = data[j];
data[j] = t;
}
}
}
}
//从键盘读入一组整数存储到数组arr中,元素个数存储到count中
void InputData( int &count, int arrt[] )
{
int i = 0, data;
while( 1 )
{
printf( "input an integer(end of 65535)" );
scanf( "%d", &data );
if( data == 65535 )
{
break;
}
else
{
arrt[++i] = data;
}
}
count = i;
}
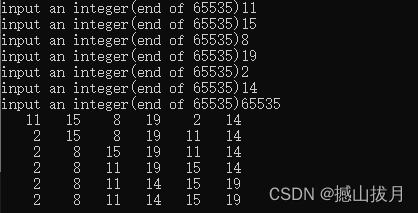
3.测试用例
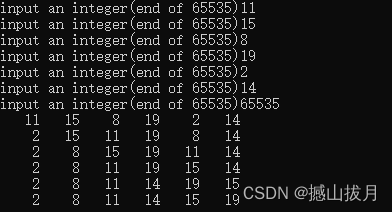
四、算法改进
上述算法中,两层循环里的操作是数据交换。事实上,对于每个固定的i,其实是从data[i]到data[n]中寻找最小值,在寻找最小值的过程中可能会发生多次数据交换,这其实降低了算法的执行效率。解决这个问题的其中一个方法是只把data[i]和最小值交换一次,具体实现方法就是把data[i]存放到data[0],然后每次遇到小于data[0]的元素就将其存放到data[0]中,同时记录其位置下标loc,最后把data[0]中元素存入data[i],把data[i]存入data[loc]即可。此法可以有效提高排序的效率。
具体算法实现如下:
void SelectionSort( int data[], int n )
{
int i, j, t, k, loc;
for( i = 1; i <= n-1; i++ )
{
data[0] = data[i];
loc = 0;
//输出每一轮排序前的状态
for( k = 1; k <= n; k++ )
{
printf( "%5d", data[k] );
}
printf( "\n" );
//排序
for( j = i+1; j <= n; j++ )
{
if( data[j] < data[0] )
{
data[0] = data[j];
loc = j;
}
}
if( loc > i )
{
data[loc] = data[i];
data[i] = data[0];
}
}
}
测试二