目录
一、算法
1.1 基本特征
有穷性、确定性、可行性。
1.2 基本要素
对数据队形的运算和操作:算术运算(加减乘除),逻辑运算(与或非),关系运算(大于、小于、等于),数据传输(输入、输出、赋值)。
算法的控制结构:各操作间的执行顺序,描述算法的工具(传统流程图、N-S结构化流程图、算法描述语言),三种基本结构(顺序、选择、循环)的组合。
算法设计的基本方法:递推法、递归、穷举搜索法、贪婪法、分治法、动态规划法、迭代法。
1.3 算法的复杂度
时间复杂度:执行算法所需的计算工作量,即执行所需的基本运算次数。
快速判断算法复杂度方法:确定问题规模n;循环减半过程为logn;k层关于n的循环为n^k。
空间复杂度:执行算法所需的内存空间。
注意:算法的时间复杂度和空间复杂度是相互独立的。
二、数据结构的基本概念
2.1 数据逻辑的定义
数据结构(Data Structure):相互存在一种或多种特定关系的数据元素的集合。
数据(Data):对客观事物的符号表示,是数据元素的集合。
数据元素(Data Element):数据的基本单位。有时一个数据元素可由若干数据项组成。
数据项(Data item):数据的最小单位。
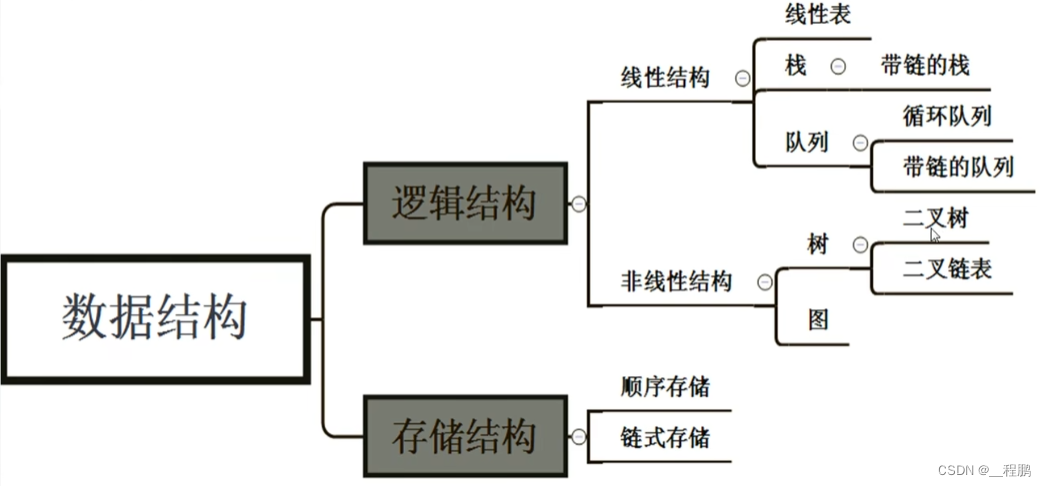
2.2 数据的逻辑结构
概念:反映数据元素之间的关系的数据元素集合的表示。
一个数据结构包含两方面信息:数据元素的信息,各数据之间的前后件关系。
如,线性结构: 有且只有一个根节点(无前件),每个节点最多只有一个前件、一个后件。
?????? 非线性结构:?? 不满足以上条件的结构,如树形结构、网状结构。
![]() ???
??? 
2.3 数据的存储结构
概念:再计算机存储空间中的存放形式。
如,顺序结构(数组)、链式存储结构(链表)。
![]() ??
?? 
三、线性表及顺序存储结构
线性表:是一个线性结构,是一个包含n≥0个结点的有限序列。
???????????? ? 既可以顺序存储,又可以链式存储。
顺序表:采用线性存储结构的线性表。
四、栈和队列
4.1 栈的定义和操作
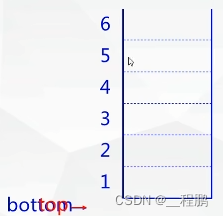
栈(Stack)的定义:限定在一端进行插入和删除的线性表。称插入和删除的一端为栈顶,另一端为栈底。栈称为“先进后出”(FILO)表或“后进先出”(LIFO)表。
栈的操作:入栈运算、出栈运算、读栈顶元素。
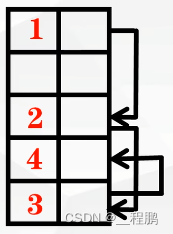
入栈运算:在栈顶位置插入一个新元素。即先栈顶指针加1,再将元素插入到栈顶指针指向位置。
出栈运算:取出栈顶元素并赋给一个指定的变量。即先栈顶元素赋给指定变量,再栈顶指针减1。
读栈顶元素:将栈顶元素赋给一个指定的变量。
注意: 栈空间已满,不能进行入栈操作了,称为“上溢”错误。
? ? ? ? ? ? 栈空间没有元素,不能进行出栈操作了,称为“下溢”错误。
? ? ? ? ? ?栈顶指针变化,栈底指针不变。
 ????
???? 
4.2 队列的定义和操作
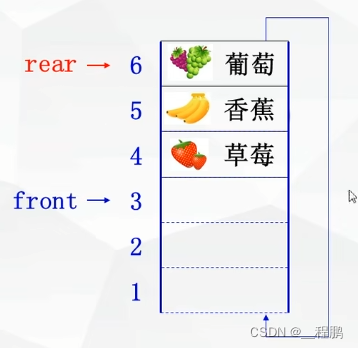
队列(Queue)的定义:限定在一个删除,在另一端插入的顺序表。允许删除的一端叫做队头(Front),允许插入的一端叫做队尾(Rear)。
队列称为“先进先出”线性表(FIFO)或“后进后出”(LILO)线性表。
队列操作:入队操作、出队操作。
入队操作:往队列队尾插入一个元素。
出队操作:往队列队头删除一个元素。
注意:栈顶指针和栈底指针都会变化。

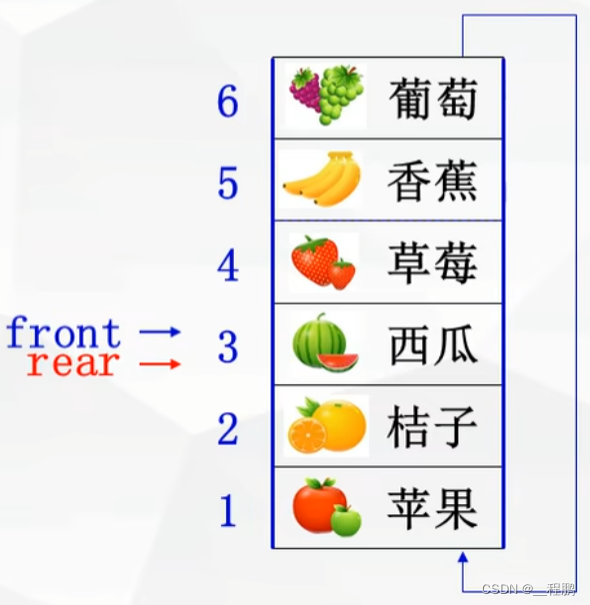
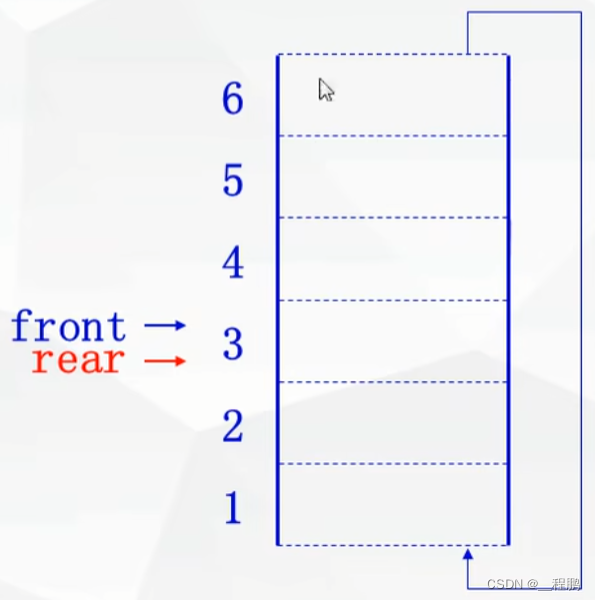
循环队列的定义:将队列存储空间的最后一个位置绕道第一个位置,形成逻辑上的环状空间。队尾指针Rear指向队列中的队尾元素,队头指针Front指向排头元素的前一个位置。
入队运算:在循环队列的队尾加入一个元素。
退队运算:在循环队列的队头位置推出一个元素并赋给指定变量。
计算循环队列内元素个数的公式:

举例:
 ??
??  ??
?? ?
?
五、线性链表
5.1 链表
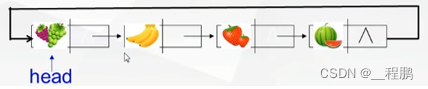
概念:在定义的链表中,只含有一个指针域来存放下一个元素地址的链表称为单链表或线性链表。
每个结点由两部分组成:??? 一部分是用于存放数据元素值,称为数据域;
???????????????????????????????????????????一部分是用于存放指针,称为指针域。

线性表顺序存储结构和链式存储结构操作对比
查找操作:查找过程从开始结点出发,顺着链表逐个将结点的值和给定x做比较。因此就对于该操作,线性链表比顺序表慢很多
插入操作:线性链表比顺序表方便。

删除操作:线性链表比顺序表方便。

5.2 双向链表

5.3 循环链表
六、树与二叉树
6.1树的定义
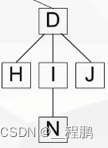
树的定义:由n(n≥0)个结点组成的有限集合。有且仅有一个称为根的元素;其余元素是互不相交的子树;n=0为空树。

- ①如A是B、C、D的父结点; B、C、D是A的子结点。
- ②根结点(无前件):A; 叶子结点(无后件):K、L、M、N。
- ③B结点的度(拥有后件的个数):2; 树的度(所有结点最大的度):3。
- ④树的深度(层数,根也算一层):4。
⑤子树: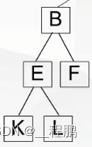 、
、![]() 、
、 均是
均是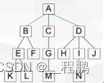 的子树
的子树
6.2 二叉树的定义和性质
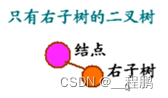
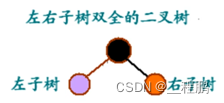
二叉树的定义:由n(n≥0)个结点的有限集合过后成,此集合或者为空集,或者由一个根结点及两棵互不相交的左右子树组成,并且左右子树都是二叉树。
 、
、 、
、 、
、 、
、
满二叉树:除最后一层外,每一层上的所有结点都有两个子结点。
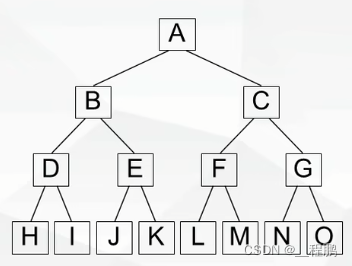
完全二叉树:除最后一层外,每一层上的结点数均达到最大值,在最后一层上只缺少右边若干结点。
 ?
?
二叉树的基本性质:
①在二叉树的第k层上至多有![]() 个结点(k≥1);
个结点(k≥1);
②深度为m的二叉树最多有![]() 个结点;
个结点;
③度=0的结点(叶子结点)总比度=2的结点多1个。
如下图,度=0的结点:H、E、L、M、N共5个;
????? ?????? 度=2的结点:A、B、C、F共4个;
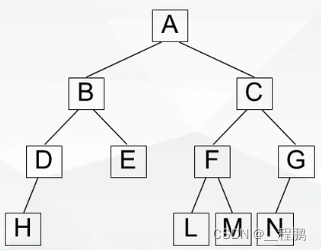
④有n个结点的二叉树深度至少为![]() ;
;
如上图,结点数为11,则二叉树深度为![]()
????? ?????? 向下取舍,得到![]()
6.3 二叉树的遍历
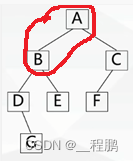
前序遍历(根左右):首先访问根结点,然后遍历左子树,最后遍历右子树。
如下图,遍历次序为:A、B、D、G、E、C、F
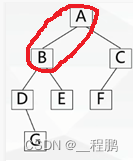



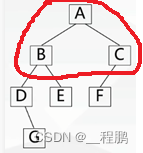
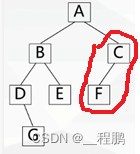
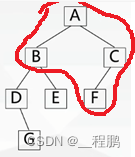
中序遍历(左根右):首先遍历左子树,然后访问根结点,最后遍历右子树。
如下图,历次序为:D、G、B、E、A、F、C
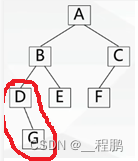
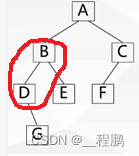
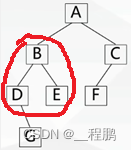

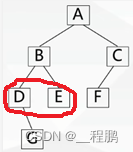
后序遍历(左右根):首先遍历左子树,然后遍历右子树,最后访问根结点。
???????????? 如下图,遍历次序为:G、D、E、B、F、C、A





七、查找技术
7.1 顺序查找
一般指在线性表中按顺序查找指定的元素。基本方法如下:
从线性表的第一个元素开始,依次将线性表中的元素与被查元素进行比较,若相等则查找成功,否则查找失败。
注意:顺序查找适用于无序表(未进行排序)或链式线性表。对长度为n的线性表,平均要进行n/2次比较,最多要进行n次比较,效率低下。
7.2 二分法查找
一般指在线性表中按二分法查找指定的元素。基本方法如下:
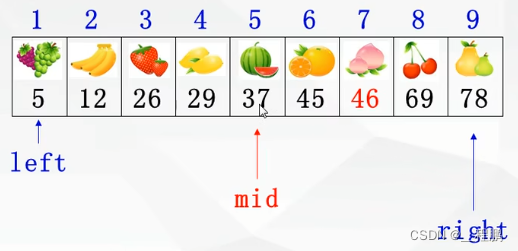 ?
? ?
?
注意:二分法查找适用于顺序存储的有序表。对长度为n的线性表,最多进行![]() 次比较。
次比较。
八、排序技术
8.1 插入排序
排序方法:每次将一个待排序的元素插入到前面已经排好序的序列中,使序列依然有序,直到待排序元素全部插入完为止。
8.2 选择排序
排序方法:从序列中找出最小(或最大)的元素,与未排序序列的第一个元素交换,直到全部元素排完。
例如:序列为66,13,51,76,81,26,57,69,23,以第1个元素为划分基准。
第1步:最小是13,交换得13,66,51,76,81,26,57,69,23
第2步:最小是23,交换得13,23,51,76,81,26,57,69,66
第3步:最小是26,交换得13,23,26,76,81,51,57,69,66
第4步:最小是51,交换得13,23,26,51,81,76,57,69,66
第5步:最小是57,交换得13,23,26,51,57,76,81,69,66
第6步:最小是66,交换得13,23,26,51,57,66,81,69,76
第7步:最小是69,交换得13,23,26,51,57,66,69,81,76
第8步:最小是76,交换得13,23,26,51,57,66,69,76,81
8.3 冒泡排序
排序方法:两两比较待排序元素的大小,发现两个元素的次序相反时即进行交换,直到没有反序元素为止。
8.3 快速排序
例如:序列为66,13,51,76,81,26,57,69,23,以第1个元素为划分基准。
第1步:66>23,交换得23,13,51,76,81,26,57,69,66
第2步:13<66,51<66,76>66,交换得23,13,51,66,81,26,57,69,76
第3步:66<69,66>57,交换得23,13,51,57,81,26,66,69,76
第4步:81>66,交换得23,13,51,57,66,26,81,69,76
第5步:66>26,交换得23,13,51,57,26,66,81,69,76
元素66到了中间正确的位置,两边的两组序列再使用该方法分别进行排序,直到完成排序任务。
8.5 其他排序
