[数据结构与算法]Hash，位图，布隆过滤器

哈希概念

顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素
时，必须要经过关键码的多次比较。顺序查找时间复杂度为O(N)，平衡树中为树的高度，即O($lo{g}_{2}N$)，搜索的效率取决于搜索过程中元素的比较次数 。而我们知道数组即顺序表的随机访问是非常快的，如果我们存放的元素能和数组下标建立关系，那么查询效率可以达到理想极致的0(1).

理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。如果构造一种存储结构，通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立
一一映射的关系，那么在查找时通过该函数可以很快找到该元素

当向该结构中

• 插入元素

  ? 根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放

• 搜索元素

  ? 对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置
  取元素比较，如果元素相等，则搜索成功

该方式即为哈希(散列)方法，哈希方法中使用的转换函数称为哈希(散列)函数，构造出来的结构称为哈希表(Hash Table)(或者称散列表)

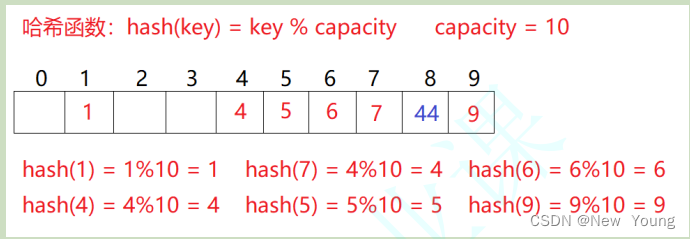
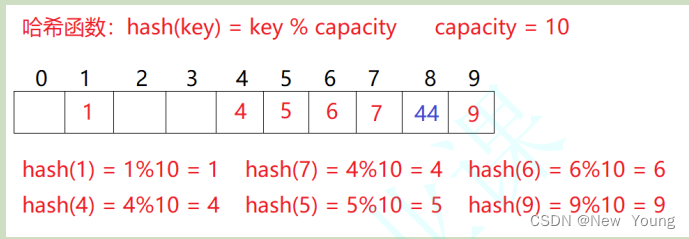
例如：数据集合{1，7，6，4，5，9}；
哈希函数(hashFunc)设置为：hash(key) = key % sz; sz为开辟空间的大小.

用该方法进行搜索不必进行多次关键码的比较，因此搜索的速度比较快
问题：按照上述哈希方式，向集合中插入元素44，会出现什么问题 ？

会出现下标为4的位置已经有元素存储了，那么44该怎么存储呢?-----这种现象称为哈希冲突

哈希冲突

对于不同的关键子，通过同一个哈希函数，映射到同一位置的现象称为为哈希冲突/哈希碰撞。把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。

哈希函数

1. 哈希函数设计的越精妙，产生哈希冲突的可能性就越低，但是无法避免哈希冲突
2. 引起哈希冲突的一个原因可能是：哈希函数设计不够合理。
   哈希函数设计原则：

1. 哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值域必须在0到m-1之间
2. 哈希函数计算出来的地址能均匀分布在整个空间中
3. 哈希函数应该比较简单

除留余数法–(非常常用)

1. 设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，
   按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址
2. 由于%的特性，除留余数法在哈希分割文件，布隆过滤器等都有使用

直接定址法–(常用)

取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B
优点：简单、均匀
缺点：需要事先知道关键字的分布情况
使用场景：适合查找比较小且连续的情况

平方取中法–(了解)

假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况

折叠法–(了解)

折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况

随机数法–(了解)

选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中random为随机数函数。通常应用于关键字长度不等时采用此法

数学分析法–(了解 ）

**设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各位上出现的频率不一定相同，可能在某些位上分布比较均匀，每种符号出现的机会均等，在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小，选择其中各种符号分布均匀的若干位作为散列地址。**例如：

假设要存储某家公司员工登记表，如果用手机号作为关键字，那么极有可能前7位都是 相同的，那么我们可以选择后面的四位作为散列地址，如果这样的抽取工作还容易出现 冲突，还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移
位、前两数与后两数叠加(如1234改成12+34=46)等方法。数字分析法通常适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布较均匀的情况

哈希冲突解决

解决哈希冲突两种常见的方法是：闭散列和开散列

实际中更多的是使用开散列 解决哈希冲突。

闭散列

闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置 ？

线性探测与二次探测

线性探测

线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止

插入
通过哈希函数获取待插入元素在哈希表中的位置.如果该位置中没有元素则直接插入新元素，如果该位置中有元素发生哈希冲突，使用线性探测找到下一个空位置，插入新元素 .

如插入44

删除：

采用闭散列处理哈希冲突时，不能随便物理删除哈希表中已有的元素，若直接删除元素会影响其他元素的搜索。比如删除元素4，如果直接删除掉，44查找起来可能会受影响。因此线性探测采用状态法标记的伪删除法来删除一个元素。

enum   Status
{
EMPTY,
DELETE,	 
EXIT
};

二次探测
线性探测的缺陷是产生冲突的数据堆积在一块，这与其找下一个空位置有关系，因为找空位
置的方式就是挨着往后逐个去找，因此二次探测为了避免该问题，找下一个空位置的方法
为：$H_i$ = ($H_0$ + $i^2$ )% m, 或者：$H_i$ = ($H_0$ - $i^2$ )% m。其中：i =
1,2,3…， $H_0$是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置，m是表的大小。
对于2.1中如果要插入44，产生冲突，使用解决后的情况为：

研究表明：当表的长度为质数且表装载因子a不超过0.5时，新的表项一定能够插入，而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置，就不会存在表满的问题。在
搜索时可以不考虑表装满的情况，但在插入时必须确保表的装载因子a不超过0.5，如果超出必须考虑增容。

闭散列最大的缺陷就是空间利用率比较低，这也是哈希的缺陷

闭散列代码

关键码函数

很明显当关键码是整形时，通过哈希映射非常简单，但是对于字符串类呢?

我们可以通过某个函数来获得字符串对应的整形，毕竟字符是一种asicc码。

template<class K>
struct DefaultHashFun
{
	size_t operator()(const K&k)
	{
		return k;
	}
};
//特化
template<>
struct DefaultHashFun <string>
{
	size_t operator()(const string& str)
	{
		size_t Hashi = 0;
		for (auto e : str)
		{
			Hashi = Hashi * 131 + e;
		}
		return Hashi;
	}
};

扩容

当数组接近满时，闭散列的插入发生冲突的概率会逐渐变大，因此我们一把通过负载因子来控制数组的扩容。

负载因子=有效的元素个数/散列表的长度

if (_table.size()==0 || (double)_n / (double)_table.size() >0.7)
		{
		//扩容
			int newsize = _table.size() == 0 ? 10 : 2 * _table.size();

			HashTable newHT;
			newHT._table.resize(newsize);
			for (auto & e : _table)
			{
				if (e._status == EXIT)
				{
					newHT.Insert(e._kv);
				}	
			}
			newHT._table.swap(_table);
		}

插入

bool Insert(const pair<K, V>& kv)
	{
		if (_table.size()==0 || (double)_n / (double)_table.size() >0.7)
		{
		//扩容
			int newsize = _table.size() == 0 ? 10 : 2 * _table.size();

			HashTable newHT;
			newHT._table.resize(newsize);
			for (auto & e : _table)
			{
				if (e._status == EXIT)
				{
					newHT.Insert(e._kv);
				}	
			}
			newHT._table.swap(_table);
		}

		int Hashi = DHF()(kv.first) % _table.size();
		int i = 1;
		while (_table[Hashi]._status == EXIT)
		{
			Hashi = Hashi + i * i;//二次探测
			++i;
			Hashi%= _table.size();
		}
		_table[Hashi]._kv = kv;
		_table[Hashi]._status = EXIT;
		++_n;
		return true;
	}

删除

bool Erase(const K& k)
	{
		auto ret = Find(k);
		if (ret)
		{
			ret._status = DELETE;
			--_n;
			return true;
		}
		else
		{
			return false;
		}
	}

find

data* Find(const K&k)
	{
		if (_table.size() == 0)
		{
			return nullptr;
		}
		int Hashi = DHF()(k) % _table.size();
		int i = 1;
		//有负载因子存在，不会死循环
		while (_table[Hashi]._status!= EMPTY)
		{
			if (_table[Hashi]._status != DELETE && _table[Hashi]._kv.first == k)
			{
				return &_table[Hashi];
			}
			Hashi = Hashi + i*i;//二次探测
			++i;
			Hashi %= _table.size();
		}
		return nullptr;
	}

全部代码

enum   Status
{

	EMPTY,
	DELETE,
	EXIT
};
template<class K, class V>
struct  HashData
{
	
	pair<K,V> _kv= pair<K, V>();
	Status _status = EMPTY;
};
template<class K>
struct DefaultHashFun
{
	size_t operator()(const K&k)
	{
		return k;
	}
};
//特化
template<>
struct DefaultHashFun <string>
{
	size_t operator()(const string& str)
	{
		size_t Hashi = 0;
		for (auto e : str)
		{
			Hashi = Hashi * 131 + e;
		}
		return Hashi;
	}
};

template<class K,class V,class DefaultHashFun>
class HashTable
{
	
public:
	typedef   HashData<K, V> data;
	typedef   DefaultHashFun DHF;
	bool Insert(const pair<K, V>& kv)
	{
		if (_table.size()==0 || (double)_n / (double)_table.size() >0.7)
		{
		//扩容
			int newsize = _table.size() == 0 ? 10 : 2 * _table.size();

			HashTable newHT;
			newHT._table.resize(newsize);
			for (auto & e : _table)
			{
				if (e._status == EXIT)
				{
					newHT.Insert(e._kv);
				}	
			}
			newHT._table.swap(_table);
		}

		int Hashi = DHF()(kv.first) % _table.size();
		int i = 1;
		while (_table[Hashi]._status == EXIT)
		{
			Hashi = Hashi + i * i;//二次探测
			++i;
			Hashi%= _table.size();
		}
		_table[Hashi]._kv = kv;
		_table[Hashi]._status = EXIT;
		++_n;
		return true;
	}
	data* Find(const K&k)
	{
		if (_table.size() == 0)
		{
			return nullptr;
		}
		int Hashi = DHF()(k) % _table.size();
		int i = 1;
		//有负载因子存在，不会死循环
		while (_table[Hashi]._status!= EMPTY)
		{
			if (_table[Hashi]._status != DELETE && _table[Hashi]._kv.first == k)
			{
				return &_table[Hashi];
			}
			Hashi = Hashi + i*i;//二次探测
			++i;
			Hashi %= _table.size();
		}
		return nullptr;
	}

	bool Erase(const K& k)
	{
		auto ret = Find(k);
		if (ret)
		{
			ret._status = DELETE;
			--_n;
			return true;
		}
		else
		{
			return false;
		}
	}
private:
	vector<data> _table;
	size_t _n=0;//有效数据的个数
};

开散列

1.开散列是：指针数组加链表的结合，空间利用率非常高，而且很好控制

2. 开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中
3. 开散列中每个桶中放的都是发生哈希冲突的元素

开散列中每个桶中放的都是发生哈希冲突的元素

代码

Insert

1.桶的个数是一定的，随着元素的不断插入，每个桶中元素的个数不断增多，极端情况下，可能会导致一个桶中链表节点非常多，会影响的哈希表的性能，因此在一定条件下需要对哈希表进行增容，那该条件怎么确认呢？开散列最好的情况是：每个哈希桶中刚好挂一个节点，再继续插入元素时，每一次都会发生哈希冲突，因此，在元素个数刚好等于桶的个数时，可以给哈希表增容。

2. 当扩容时，我们需要重新哈希，可以选择一个一个重新插入，也可以选择直接使用利用原始数组中的旧数据，重新哈希即可

pair <iterator ,bool>Insert(const T&data)
		{
			//移动节点
			auto pos = Find(KFT()(data));
			if (pos!=end())
				return make_pair(pos, false);
			size_t sz = _table.size();
		
			if (_n ==sz)
			{
				size_t newsize =sz == 0 ? 10 : 2 * sz;
				Self HT;
				HT._table.resize(newsize, 0);
				for (size_t i = 0; i < sz; ++i)
				{
					Node* cur = _table[i];
					while (cur)
					{
						int Hashi = HF()(KFT()(cur->_data)) % newsize;
						cur->_next = HT._table[Hashi];
						HT._table[Hashi] = cur;
						cur = cur->_next;
					}
					_table[i] = nullptr;//防止浅拷贝,局部变量释放时的的野指针问题
				}
				HT._table.swap(_table);
			}
			int Hashi = HF()(KFT()(data)) % _table.size();
			Node* newNode = new Node(data);
			newNode->_next = _table[Hashi];
			_table[Hashi] = newNode;
			++_n;
			return make_pair(iterator(newNode, this), true);
		}

Find

iterator Find(const K& key)
		{
			if (_table.size() == 0)
			{
				return iterator(nullptr, this);
			}
			int sz = _table.size();
			int Hashi = HF()(key) % sz;
			Node* cur = _table[Hashi];
			while (cur && KFT()(cur->_data) != key)
			{
				cur = cur->_next;
			}
			return iterator(cur, this);
		}

Erase

bool Erase(const K& key)
		{
			assert(_table.size());

			int Hashi = HF()(key) % _table.size();
			Node* pre = nullptr;
			Node* cur = _table[Hashi];
			while (cur)
			{
				if (KFT()(cur->_data) == key)
				{
					if (pre == nullptr)
					{
						_table[Hashi] = cur->_next;
					}
					else
					{
						pre->_next = cur->_next;

					}
					delete cur;
					--_n;
					return true;
				}
				else
				{
					pre = cur;
					cur = cur->_next;
				}
			}
			return false;
		}

迭代器

当前桶访问完时，我们要计算下一个桶，而节点的地址我们知道了，可以直接确定当前桶的位置，为了确定下一个非空桶，我们需要一个指向哈希表的指针

同时为了访问方便，我们还需要将迭代器在哈希表中内置为友元类

template<class K, class Ref, class Ptr, class T, class KeyOfType, class HashFunc = DefaultHashFunc<K> >
	class  HT_Iterator
	{

	public:
		typedef HashNode<T>  Node;
		typedef KeyOfType KFT;
		typedef HashFunc HF;
		typedef my_hash::HT_Iterator<K, Ref, Ptr, T, KFT, HF> Self;
		typedef my_hash::HashTable<K, T, KFT, HF> HT;
		HT_Iterator() = default;
		HT_Iterator(Node* node = nullptr, const HT* ht = nullptr)
			:_node(node), _ht(ht)
		{
			;
		}
		HT_Iterator(const Self& self)
		{
			_node = self._node;
			_ht = self._ht;
		}
		Self& operator++()
		{

			Node* pre = _node;
			_node = _node->_next;
			if (_node == nullptr)
			{
				size_t Hashi = HF()(KFT()(pre->_data)) % _ht->_table.size();
				while (_node == nullptr && ++Hashi < _ht->_table.size())
				{
					_node = _ht->_table[Hashi];
				}
				if (Hashi == _ht->_table.size())
				{
					_node = nullptr;
				}
			}
			return *this;
		}
		Ref operator*()
		{
			return _node->_data;
		}
		Ptr operator->()
		{
			return &_node->_data;
		}

		bool operator==(const Self& self)
		{
			return _node == self._node;
		}
		bool operator!=(const Self& self)
		{
			return _node != self._node;
		}

		Node* _node;
		const HT* _ht;

	};

全部代码

namespace my_hash
{

	template<class K>
	struct DefaultHashFunc
	{
		size_t operator()(const K& k)
		{
			return k;
		}
	};
	//特化
	template<>
	struct DefaultHashFunc <string>
	{
		size_t operator()(const string& str)
		{
			size_t Hashi = 0;
			for (auto e : str)
			{
				Hashi = Hashi * 131 + e;
			}
			return Hashi;
		}
	};

	template<class T>
	struct HashNode
	{
		HashNode(const T& data = T())
			:_data(data)
		{
		}
		T _data;
		HashNode* _next = nullptr;

	};

	template<class K, class T, class KeyOfType, class HashFunc = DefaultHashFunc<K>>
	class HashTable;//声明，方便迭代器中定义Hash表的指针

	template<class K, class Ref, class Ptr, class T, class KeyOfType, class HashFunc = DefaultHashFunc<K> >
	class  HT_Iterator
	{

	public:
		typedef HashNode<T>  Node;
		typedef KeyOfType KFT;
		typedef HashFunc HF;
		typedef my_hash::HT_Iterator<K, Ref, Ptr, T, KFT, HF> Self;
		typedef my_hash::HashTable<K, T, KFT, HF> HT;
		HT_Iterator() = default;
		HT_Iterator(Node* node = nullptr, const HT* ht = nullptr)
			:_node(node), _ht(ht)
		{
			;
		}
		HT_Iterator(const Self& self)
		{
			_node = self._node;
			_ht = self._ht;
		}
		Self& operator++()
		{

			Node* pre = _node;
			_node = _node->_next;
			if (_node == nullptr)
			{
				size_t Hashi = HF()(KFT()(pre->_data)) % _ht->_table.size();
				while (_node == nullptr && ++Hashi < _ht->_table.size())
				{
					_node = _ht->_table[Hashi];
				}
				if (Hashi == _ht->_table.size())
				{
					_node = nullptr;
				}
			}
			return *this;
		}
		Ref operator*()
		{
			return _node->_data;
		}
		Ptr operator->()
		{
			return &_node->_data;
		}

		bool operator==(const Self& self)
		{
			return _node == self._node;
		}
		bool operator!=(const Self& self)
		{
			return _node != self._node;
		}

		Node* _node;
		const HT* _ht;

	};

	template<class K, class T, class KeyOfType, class HashFunc>
	class HashTable
	{
		typedef HashNode<T>  Node;
		typedef HashFunc HF;
		typedef KeyOfType KFT;
		typedef HashTable<K, T, KFT, HF> Self;
		template<class K, class Ref, class Ptr, class T, class KeyOfType, class HashFunc >
		friend class  HT_Iterator;
	public:
		typedef  my_hash::HT_Iterator<K, T&, T*, T, KFT, HF> iterator;
		typedef  my_hash::HT_Iterator<K, const T&, const T*, T, KFT, HF> const_iterator;
		iterator begin()
		{
			size_t i = 0;
			for (; i < _table.size(); ++i)
			{
				if (_table[i])//第一个非空通
				{
					return iterator(_table[i], this);
				}
			}
			return end();
		}
		iterator end()
		{
			return iterator(nullptr, this);
		}
		const_iterator  begin()const
		{
			size_t i = 0;
			for (; i < _table.size(); ++i)
			{
				if (_table[i])//第一个非空通
				{
					return const_iterator(_table[i], this);
				}
			}
			return end();

		}
		const_iterator end()const
		{
			return const_iterator(nullptr, this);
		}
	public:
		HashTable() = default;
		HashTable(const Self& HT)
			//需要深拷贝
		{
			int sz = HT._table.size();
			for (int i = 0; i < sz; ++i)
			{
				Node* cur = HT._table[i];
				while (cur)
				{
					Insert(cur->_kv);
					cur = cur->_next;
				}
			}
			_n = HT._n;
		}
		Self& operator=(Self HT)
		{
			HT._table.swap(_table);
			_n = HT._n;

			return *this;
		}
		~HashTable()
		{
			for (size_t i = 0; i < _table.size(); ++i)
			{
				Node* cur = _table[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_table[i] = nullptr;
			}
		}

		//插入
		pair <iterator ,bool>Insert(const T&data)
		{
			//移动节点
			auto pos = Find(KFT()(data));
			if (pos!=end())
				return make_pair(pos, false);
			size_t sz = _table.size();
		
			if (_n ==sz)
			{
				size_t newsize =sz == 0 ? 10 : 2 * sz;
				Self HT;
				HT._table.resize(newsize, 0);
				for (size_t i = 0; i < sz; ++i)
				{
					Node* cur = _table[i];
					while (cur)
					{
						int Hashi = HF()(KFT()(cur->_data)) % newsize;
						cur->_next = HT._table[Hashi];
						HT._table[Hashi] = cur;
						cur = cur->_next;
					}
					_table[i] = nullptr;//防止浅拷贝,局部变量释放时的的野指针问题
				}
				HT._table.swap(_table);
			}
			int Hashi = HF()(KFT()(data)) % _table.size();
			Node* newNode = new Node(data);
			newNode->_next = _table[Hashi];
			_table[Hashi] = newNode;
			++_n;
			return make_pair(iterator(newNode, this), true);
		}
		iterator Find(const K& key)
		{
			if (_table.size() == 0)
			{
				return iterator(nullptr, this);
			}
			int sz = _table.size();
			int Hashi = HF()(key) % sz;
			Node* cur = _table[Hashi];
			while (cur && KFT()(cur->_data) != key)
			{
				cur = cur->_next;
			}
			return iterator(cur, this);
		}
		bool Erase(const K& key)
		{
			assert(_table.size());

			int Hashi = HF()(key) % _table.size();
			Node* pre = nullptr;
			Node* cur = _table[Hashi];
			while (cur)
			{
				if (KFT()(cur->_data) == key)
				{
					if (pre == nullptr)
					{
						_table[Hashi] = cur->_next;
					}
					else
					{
						pre->_next = cur->_next;

					}
					delete cur;
					--_n;
					return true;
				}
				else
				{
					pre = cur;
					cur = cur->_next;
				}
			}
			return false;
		}
	private:
		vector<Node*> _table;
		size_t _n = 0;
	};
}

闭散列与开散列比较

应用链地址法处理溢出，需要增设链接指针，似乎增加了存储开销。事实上：由于开地址法必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子a <=0.7，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间 。

unordered_set的封装

namespace my_set
{
	template<class K>
	struct KeyOfType
	{
		const K& operator()(const K& key)
		{
			return key;

		}
	};
	template<class K>
	class unorder_set
	{
		typedef  my_set::KeyOfType<K> KFT;
		typedef K T;
		typedef my_hash::DefaultHashFunc<K> HF;
	public:
		typedef typename my_hash::HashTable<K, T, KFT, HF>::const_iterator   iterator;
		typedef typename my_hash::HashTable<K, T, KFT, HF>::const_iterator   const_iterator;

		~unorder_set()
		{
			HT.~HashTable();
		}
		iterator begin()const
		{
			return HT.begin();

		}
		iterator end()const
		{
			return HT.end();
		}
		pair<iterator, bool>  Insert(const K& key)
		{
			auto p = HT.Insert(key);
			// HT不可能实现一个const版的insert，因此要间接实现
			return 	make_pair(iterator(p.first._node, p.first._ht), p.second);
		}
		bool Erase(const K& key)
		{
			return 	HT.Erase(key);
		}
		T* Find(const K& key)
		{
			return HT.Find(key);
		}



	private:
		my_hash::HashTable<K, T, KFT, HF> HT;
	};
	void SetT()
	{
		unorder_set<int> set;
		set.Insert(2);
		set.Insert(3);
		set.Insert(4);
		set.Insert(5);
		set.Insert(6);
		set.Insert(7);
		set.Insert(8);
		set.Insert(9);
		set.Insert(12);
		set.Insert(13);
		set.Insert(14);


		unorder_set<int>::iterator it = set.begin();
		unorder_set<int>::iterator it2(it);


		while (it != set.end())
		{
			cout << *it << endl;
			++it;
		}

	}
}

unordered_map的封装

#pragma once
#include "Hash.h"

namespace my_map
{
	template<class K, class V>
	struct KeyOfType
	{
		const K& operator()(const pair<const K, V>& kv)
		{
			return kv.first;
		}
	 };
	template<class K, class V>
	class unorder_map
	{
		typedef my_map::KeyOfType<K, V> KFT;
		typedef pair< K, V>  T;
		typedef my_hash::DefaultHashFunc<K> HF;
	public:
		typedef typename my_hash::HashTable<K, T, KFT, HF>::iterator iterator;
		typedef typename my_hash::HashTable<K, T, KFT, HF>::const_iterator const_iterator;
		iterator begin()
		{
			return HT.begin();
		}
		const_iterator begin()const
		{
			return HT.begin();
		}
		iterator end()
		{
			return HT.end();
		}
		const_iterator end()const
		{
			return HT.end();
		}
		~unorder_map()
		{
			HT.~HashTable();
		}
		pair<iterator, bool>  Insert(const T& data)
		{
			return 	HT.Insert(data);
		}
		V& operator[](const K& key)
		{
			return HT.Insert(make_pair(key, V())).first->second;

		}
		bool Erase(const K& key)
		{
			return 	HT.Erase(key);
		}
		T* Find(const K& key)
		{
			return HT.Find(key);
		}
	private:
		my_hash::HashTable<K, T, KFT, HF> HT;
	};
	/*void  MapT()
	{
		unorder_map<int, int> map;
		map[2] = 1;
		map[3] = 1;
		map[4] = 1;
		map[5] = 1;
		map[6] = 1;
		map[7] = 1;
		unorder_map<int, int>::iterator it = map.begin();
		while (it != map.end())
		{
			cout << it->first << " " << it->second << endl;
			++it;
		}

	}*/
	void MapT()
	{
		unorder_map<string, string> map;
		map["hello"] = "你好";
		map["word"] = "世界";
		map["helloword"] = "你好世界";
		unorder_map<string, string> ::iterator it = map.begin();
		while (it != map.end())
		{
			cout << it->first << " " << it->second << endl;
			++it;
		}
	}
}

哈希的应用！！！

位图

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】

当我们在一个海量数据范围内判断某个数是否存在时，由于不能加载到内存，二分查找不能使用。文件外排序也不行，不支持随机访问。

那么我们该怎么处理呢？

我们知道一个bite位有2种转态0/1，而表示一个数据是否存在也是2种状态，因此我们可以通过某种映射，利用一个bite位1来表示该数存在，0表示不存在。 这样当有10亿个整型数据时，因为我们无法确定最大数据到底多少，因此直接开辟2^32-1个bite也就是 500M。这样同映射我们就可以在0（1）的时间内确定一个数据是否存在

位图代码

template<size_t N>//N代表最大的数据
	class bit_set
	{
	public:
		bit_set()
		{
			_bits.resize(N / 8 + 1, 0);
		}
		void set(size_t x)//添加x
		{
			if (text(x))
				return;
			size_t i = x / 8;//在哪个字节附近
			size_t j = x % 8;//相对i的距离
			_bits[i] |= (1 << j);//，因为0这个特殊的数字，所以直接位移就是x应该的位置，将对应位置变为1
		}
		void reset(size_t x)//删除x
		{
			if (!text(x))
				return;
			size_t i = x / 8;//在哪个字节附近
			size_t j = x % 8;//相对i的距离
			_bits[i] &= ~(1 << j);
		}
		bool text(size_t x)
		{
			size_t i = x / 8;//在哪个字节附近
			size_t j = x % 8;//相对i的距离

			//&后为0说明不存在，&后大于0是说明存在
			return   _bits[i] & (1 << j);
		}
	private:
		std::vector<char> _bits;
	};

位图的应用

1. 快速查找某个数据是否在一个集合中
2. 排序 + 去重
3. 求两个集合的交集、并集等
4. 操作系统中磁盘块标记

位图的局限性

位图对于海量的整形数据的处理很方便，但是对于字符串那个类型就很难处理了，因此为了处理字符串，在位图的基础通过加上哈希函数来即布隆过滤器来处理。

布隆过滤器

1. 布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中，因此被映射到的位置的比特位一定为1。所以可以按照以下方式进行查找：分别计算每个哈希值对应的比特位置存储的是否为零，只要有一个为零，代表该元素一定不在哈希表中，否则可能在哈希表中。

2. 布隆过滤器是一种近似算法，其对于不存在的数据的判断是准确的对于存在的数据可能存在“误判"，对于这种误判就要到相应的数据系统中查找了

3. 位图越长，哈希函数越多时，发生误判的可能性会越低，该如何选择呢?

如何选择哈希函数个数和布隆过滤器长度

详情请参考：https://zhuanlan.zhihu.com/p/43263751/

布隆过滤器的代码

布隆一般处理字符串，因此默认的数据类下是string，哈希函数的个数由使用者控制。M的值也由使用者控制。

namespace my_bloomfiter
{
	struct BKDRHash
	{
		size_t operator()(const string& s)
		{
			// BKDR
			size_t value = 0;
			for (auto ch : s)
			{
				value *= 31;
				value += ch;
			}
			return value;
		}
	};
	struct APHash
	{
		size_t operator()(const string& s)
		{
			size_t hash = 0;
			for (long i = 0; i < s.size(); i++)
			{
				if ((i & 1) == 0)
				{
					hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
				}
				else
				{
					hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
				}
			}
			return hash;
		}
	};
	struct DJBHash
	{
		size_t operator()(const string& s)
		{
			size_t hash = 5381;
			for (auto ch : s)
			{
				hash += (hash << 5) + ch;
			}
			return hash;
		}
	};
	//M=(k*N)/ln2
	template<size_t M, class K=string, class HashFunc1= BKDRHash, class HashFunc2=APHash, class HashFunc3= DJBHash>
	class BloomFilter
	{
	public:

		void Set(const K& key)
		{
			//计算该值的映射位置
			size_t Hashi1 = HashFunc1()(key) % M;
			size_t Hashi2 = HashFunc2()(key) % M;
			size_t Hashi3 = HashFunc3()(key) % M;
			_bts.set(Hashi1);
			_bts.set(Hashi2);
			_bts.set(Hashi3);
		}
		bool Test(const K& key)//为真不一定就存在，但是为假就一定不存在	
		{
			//重新计算该值的映射位置
			size_t Hashi1 = HashFunc1()(key) % M;
			if (!_bts.test(Hashi1))
			{
				return false;
			}
			size_t Hashi2 = HashFunc2()(key) % M;
			if (!_bts.test(Hashi2))
			{
				return false;
			}
			size_t Hashi3 = HashFunc3()(key) % M;
			if (!_bts.test(Hashi3))
			{
				return false;
			}
			return true;//可能存在误判
		}

		
	
	private:
		bitset<M> _bts;
	};
	void TestBoolm()
	{
		//my_bloomfiter::BloomFilter < string, 44, my_bloomfiter::BKDRHash, my_bloomfiter::APHash, my_bloomfiter::DJBHash> blf;
		my_bloomfiter::BloomFilter<44> blf;
		string arr[] = { "苹果","苹果","香蕉","香蕉" ,"苹果","时间","eeeee","eeee","qqqqqq","111111"};

		for (auto e : arr)
		{
			blf.Set(e);
		}
		for (auto e : arr)
		{
			if (blf.Test(e))
			{
				cout << "存在" << e << endl;
			}
			else
			{
				cout << "不存在" << e << endl;
			}
		}
		if (blf.Test("芒果"))
		{
			cout << "存在" << "芒果" << endl;
		}
		else
		{
			cout << "不存在" << "芒果" << endl;
		}
		if (blf.Test("西瓜"))
		{
			cout << "存在" << "西瓜" << endl;
		}
		else
		{
			cout << "不存在" << "西瓜" << endl;
		}
		if (blf.Test("土豆"))
		{
			cout << "存在" << "土豆" << endl;
		}
		else
		{
			cout << "不存在" << "土豆" << endl;
		}
	}
}

布隆过滤器的优点

1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数，一般比较小)，与数据量大小无
   关
2. 哈希函数相互之间没有关系，方便硬件并行运算
3. 布隆过滤器不需要存储元素本身，在某些对保密要求比较严格的场合有很大优势
4. 在能够承受一定的误判时，布隆过滤器比其他数据结构有这很大的空间优势
5. 数据量很大时，布隆过滤器可以表示全集，其他数据结构不能
6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算

布隆过滤器缺陷

1. 有误判率，即存在假阳性(False Position)，即不能准确判断元素是否在集合中(补救方法：再
   建立一个白名单，存储可能会误判的数据)

2. 不能获取元素本身

3. 一般情况下不能从布隆过滤器中删除元素

4. 如果采用计数方式删除，可能会存在计数回绕问题

布隆过滤器的删除

布隆过滤器的任务就是过滤掉不存在的数据，如果我们要删除数据，为了不影响其它数据，采用计数的方式进行删除

将布隆过滤器中的每个比特位扩展成一个小的计数器，插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一，删除元素时，给k个计数器减一，通过多占用几倍存储空间的代价来增加删除操作。

海量数据面试题

面试题一：

给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？与上题条件相同，如何找到top K的IP？

思路:

最多的iP地址：大文件就想到了分割为小文件，但因为存在重复数据的可能，单独分分割会出问题，因此我们可以通过哈希函数将重复的数据放到同一个文化或者桶中，

如果可以通过map第一个文件的去重后建个大堆就可以找出第一个文件的次数最大的ip，之后的文件的map依次于这个堆顶元素比较，大的话就更新这个次数最大的ip

如果建立map时出现内不够问题就再次分割这个小文件，换一个哈希函数，重新上述过程，如果还是不行就进行循环，直到确定最大次数的ip。

Topk

同问题一:只是在对第一个小文件要进行topk，之后将堆顶元素与剩下文件的每一个map的节点进行比较，大于top的就替换top

面试题二：

. 1. 给定100亿个整数，设计算法找到只出现一次的整数？

? 用2个bite位可以表示4种状态，这里使用2个位图即可

template<size_t N>
	class bit_sets
	{
		bit_sets()=default;//调用自定义类型的构造函数即可
		void set(size_t x)
		{
			int bt1 = bst1.test(x);
			int bt2 = bst2.test(x);
			if (bt1 == 0 && bt2 == 0)//出现0次
			{	
							//0
				bst2.set(x);//1
				
			}
			else if (bt1 == 0 && bt2 == 1)//出现1次
			{
				bst1.set(x);  //1
				bst2.reset(x);//0
			}
			else if (bt1 == 1 && bt2 == 0)//出现2次
			{
							//1
				bst2.set(x);//1
			}
		}
		void reset(size_t x)
		{
			int bt1 = bst1.test(x);
			int bt2 = bst2.test(x);
			if (bt1 == 0 && bt2 == 0)
			{
				;
			}
			else if (bt1 == 0 && bt2 == 1) //00
			{
				bst2.reset(x);
			}
			else if (bt1 == 1 && bt2 == 0)//01
			{
				bst1.reset(x);//0
				bst2.set(x);  //1
			}
			else if (bt1 == 1 && bt2 == 1)//10
			{		
				bst2.reset(x);//
			}
		}
		bool test(size_t x)
		{
			return  bst1.text(x) || bst2.text(x);
		}
	private:
		//利用同一位置有4种情况来解决一些问题
		bit_set<N> bst1;
		bit_set<N> bst2;
	};

2. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

   

3. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

   同1

面试题三

1. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法

   近似算法：布隆过滤器

   

2. 如何扩展BloomFilter使得它支持删除元素的操作

? 同上面布隆过滤器的删除