CSDN话题挑战赛第2期
参赛话题:学习笔记
文章目录
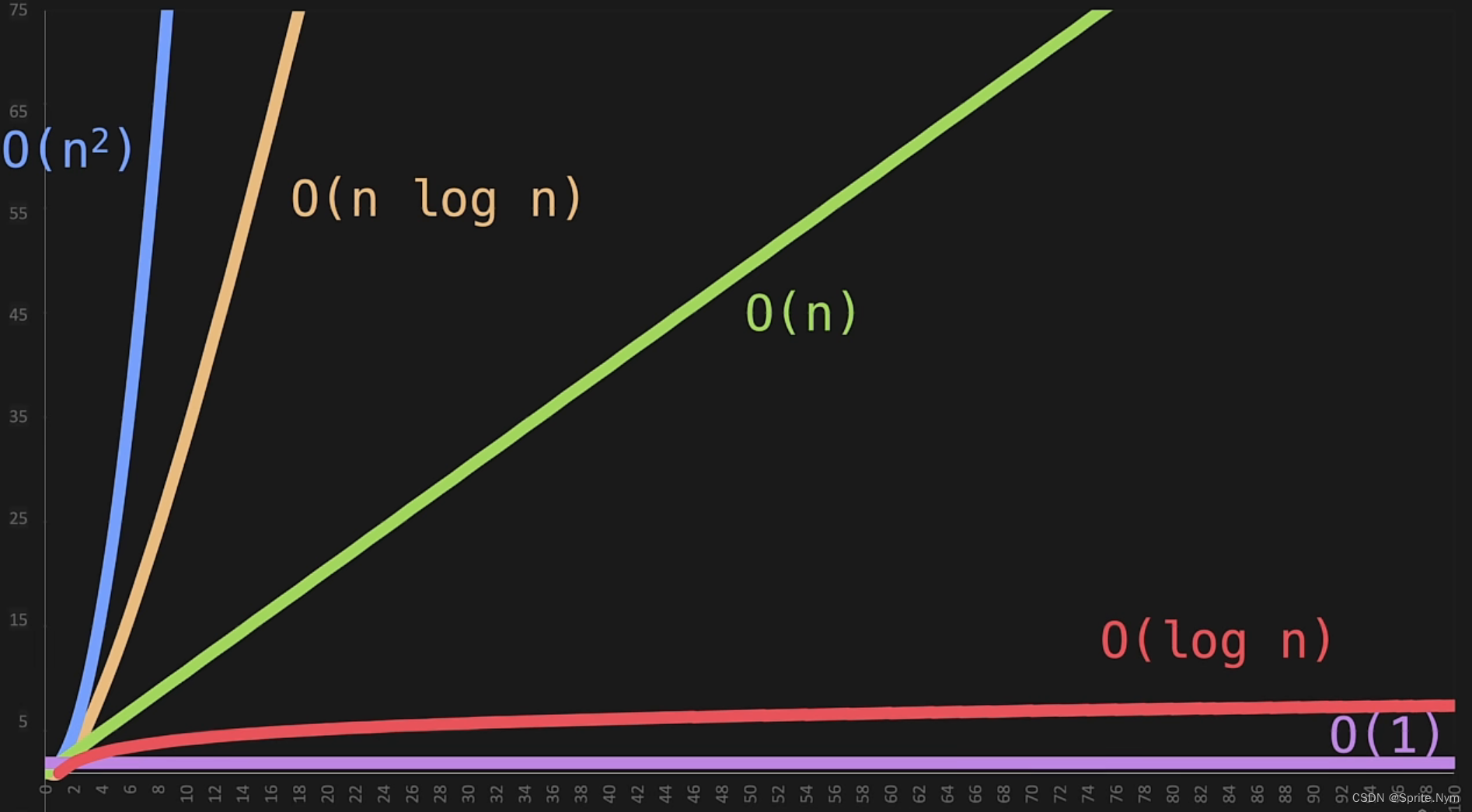
一、Big O
1.1 Big O简介
(1)分为时间复杂度和空间复杂度。
(2)三个希腊字母表示:Ω、θ、O,分别代表运行一段代码的最佳情况、平均情况和最坏情况。
所以,讨论Big O时,即是在讨论一段代码运行的最坏情况。
1.2 O(n)
(1)案例:单重循环:

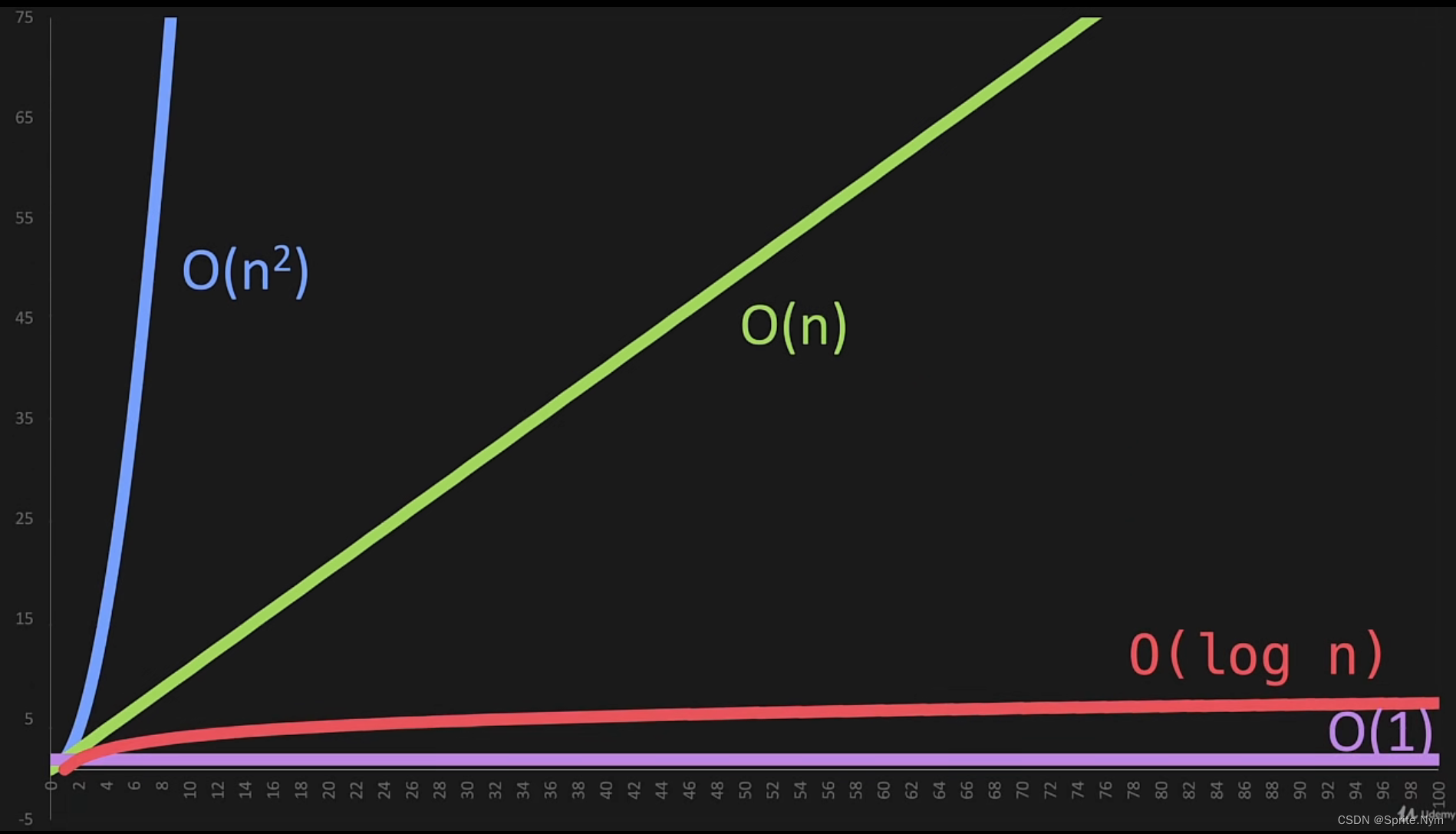
(2)O(n)的含义:x轴为n,y轴为操作的数量。O(n)即代表n和操作数量成正比。
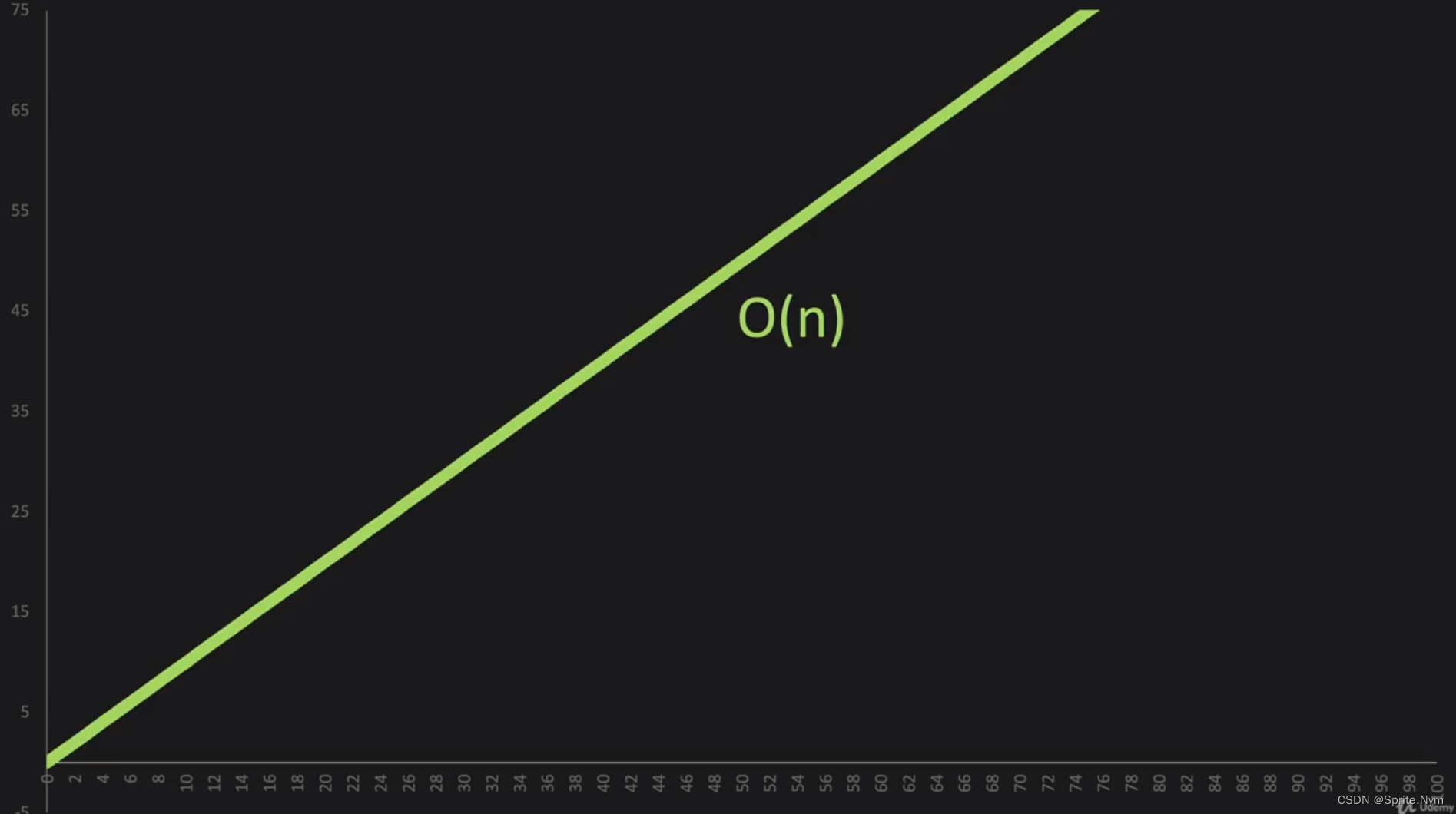
(3)丢弃常量:在讨论O(n)时,我们不关心斜率,即不关心操作数量具体是n的1倍还是2倍还是3倍,只要成正比,统统简化为O(n)。
1.3 O(n2)
(1)案例:二重循环:
(2)O(n2)的含义:x轴为n,y轴为操作的数量。O(n2)即代表操作数量与n2成正比,例如输入10要进行100次操作。
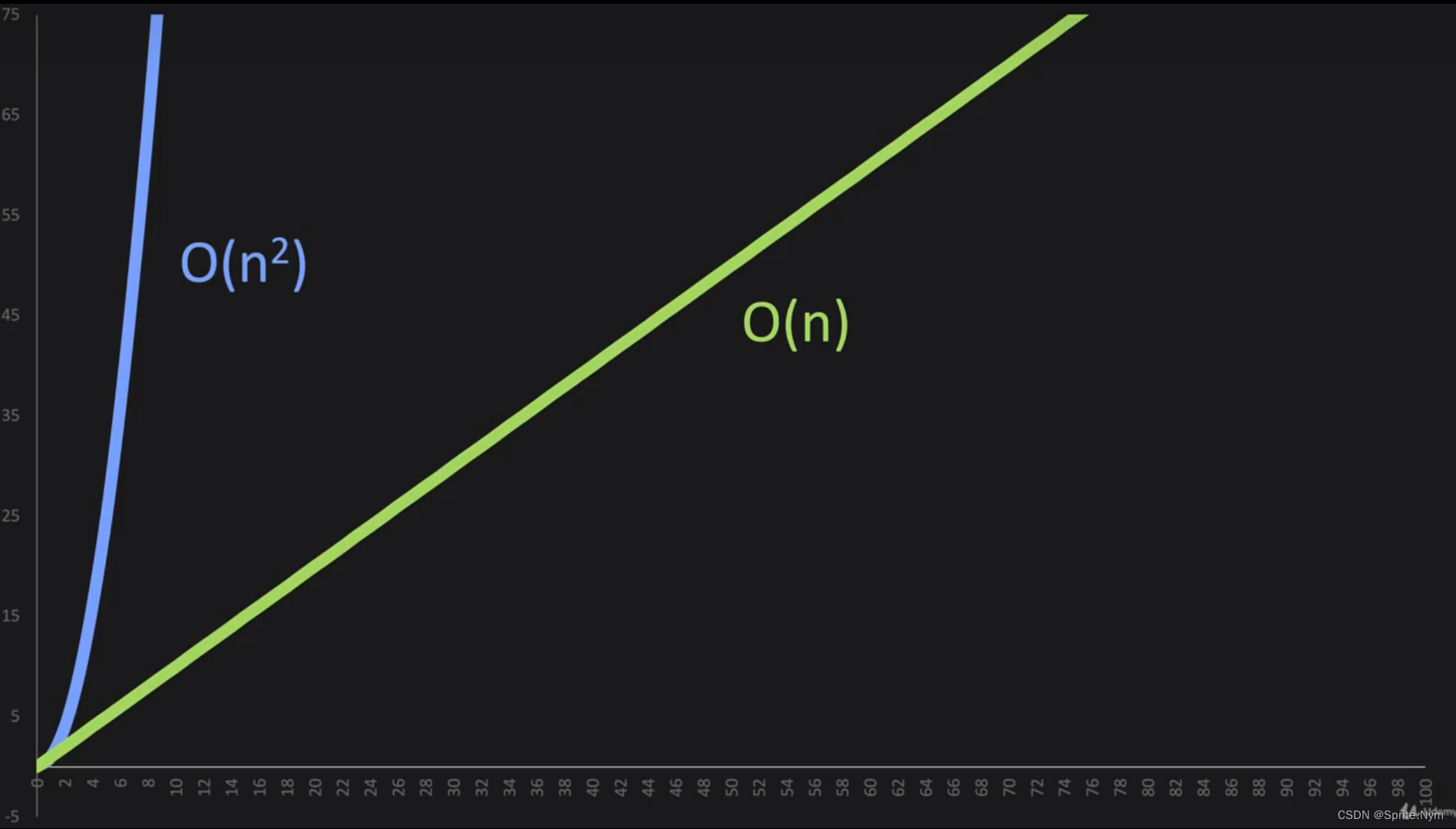
(3)丢弃非主导项:对于O(n2+n)来说,由于n和n2比起来微不足道,所以最终结果简化为O(n2)。
1.4 O(1)
(1)案例:单次求和
(2)O(1)的含义:x轴为n,y轴为操作的数量。O(1)即代表操作数量为常量,与n无关。不关心具体操作几次,只要操作数量是常量,都简化为O(1)。

1.5 O(log n)
(1)案例:在1-8的列表中二分查找1,分3次后查到1。
小学的称重找次品问题也是典型的O(log n)复杂度问题,每次三等分再称。

(2)O(log n)的含义:x轴为n,y轴为操作的数量。O(log n)即代表操作数量与log n成正比。底数是几都无所谓,均简化为O(log n)。
1.6 输入多参数的情况
如果不是只输入一个n,而是输入多个参数,则复杂度由多个参数共同决定。
例如,两个循环,一个循环a次,一个循环b次,则时间复杂度为O(a+b),而不可简化为O(n):

第二个案例同理:

1.7 列表方法的Big O
(1)列表尾部的操作:.append()和.pop():由于只涉及最后一个元素的单次操作,和列表前面有多少个元素无关,所以时间复杂度为O(1)。
(2)列表头部的操作:.pop(0)和insert(0, ):由于在头部加入或删除新元素后,后面的所有元素的索引都要重排一遍,所以时间复杂度为O(n)。
(3)列表中间的操作:在中间.pop()和.insert(),由于O讨论的是最坏的情况,同时由于复杂度不关心n前面的系数,所以时间复杂度还是O(n)。
(4)列表查找操作:遍历查找O(n),索引查找O(1)。
1.8 总结
二、链表前言
2.1 类
(1)构造函数:

(2)类中的方法:

2.2 指针
(1)不使用指针时:
num1 = 11
num2 = num1
如果num1改变了,num2保持11。
(2)使用指针时:
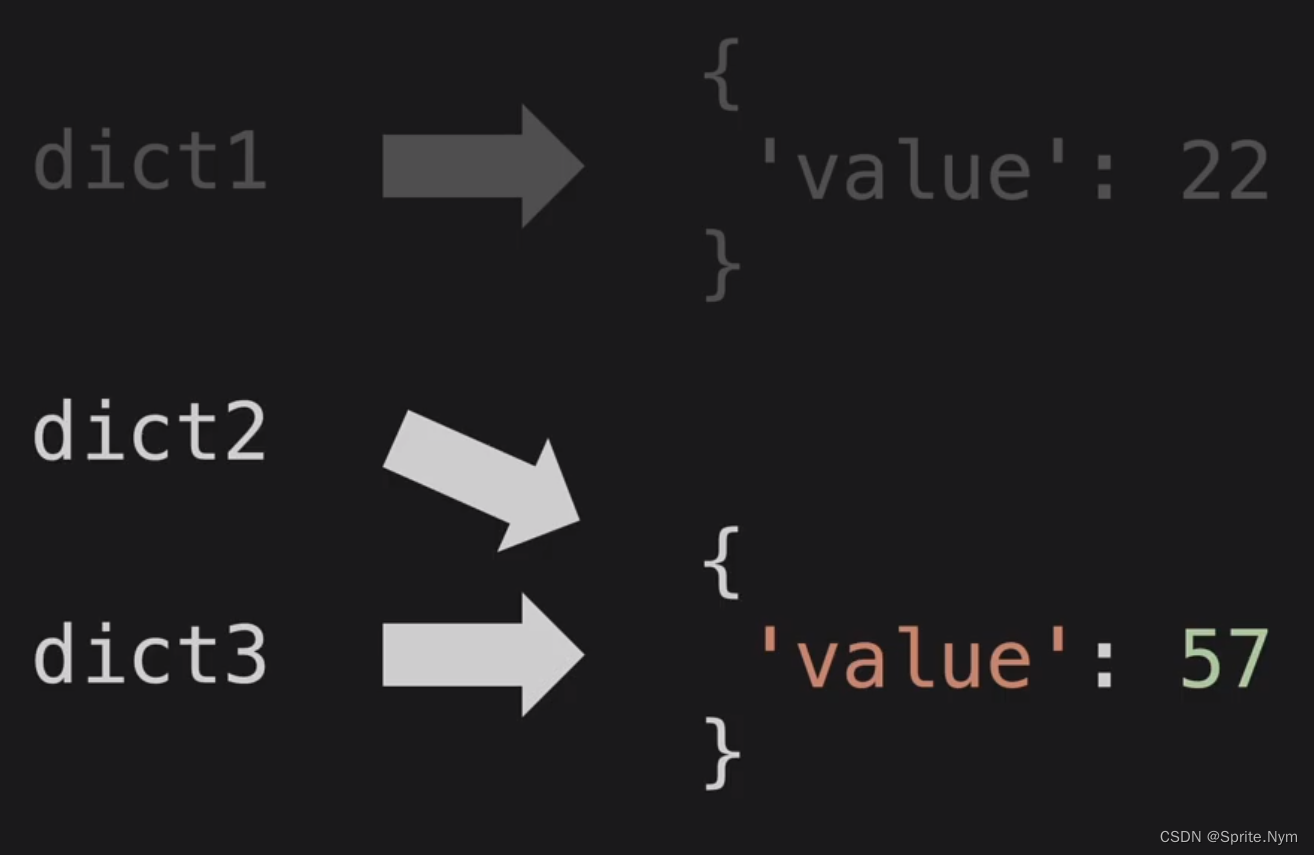
dict1 = {'value': 11}
dict2 = dict1

如果dict1更新了,dict2也会更新。
此时如果使dict2 = dict3,dict2的指针会重定向:
(3)如果所有指针都从某个内存地址移开,就再也无法定位到该地址了,Python就会使用Garbage Collection来释放内存。
< br>
三、单向链表
3.1 链表简介
| 列表 | 链表 | |
|---|---|---|
| 索引 | 有 | 无 |
| 内存地址 | 连续 | 不连续 |
链表结构示意图:
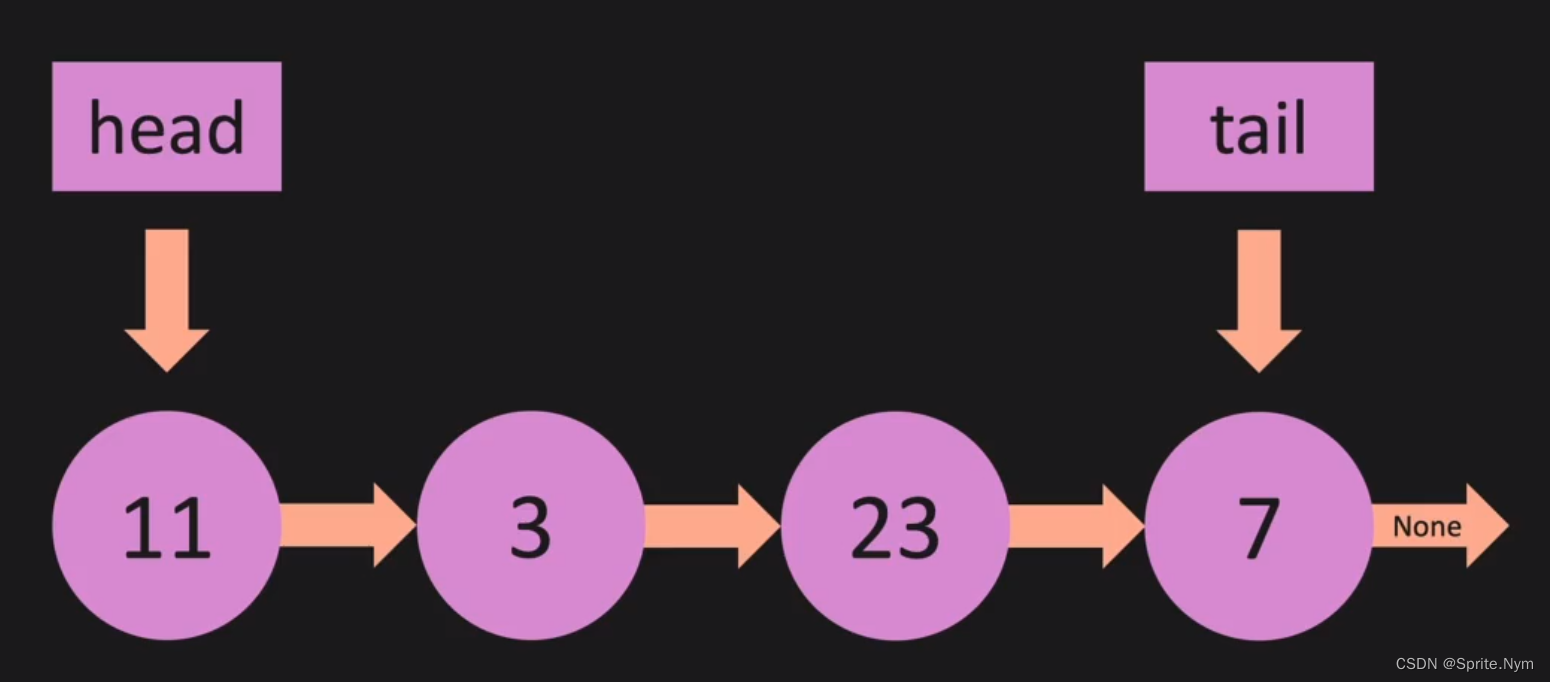
链表实际在内存中的情况:
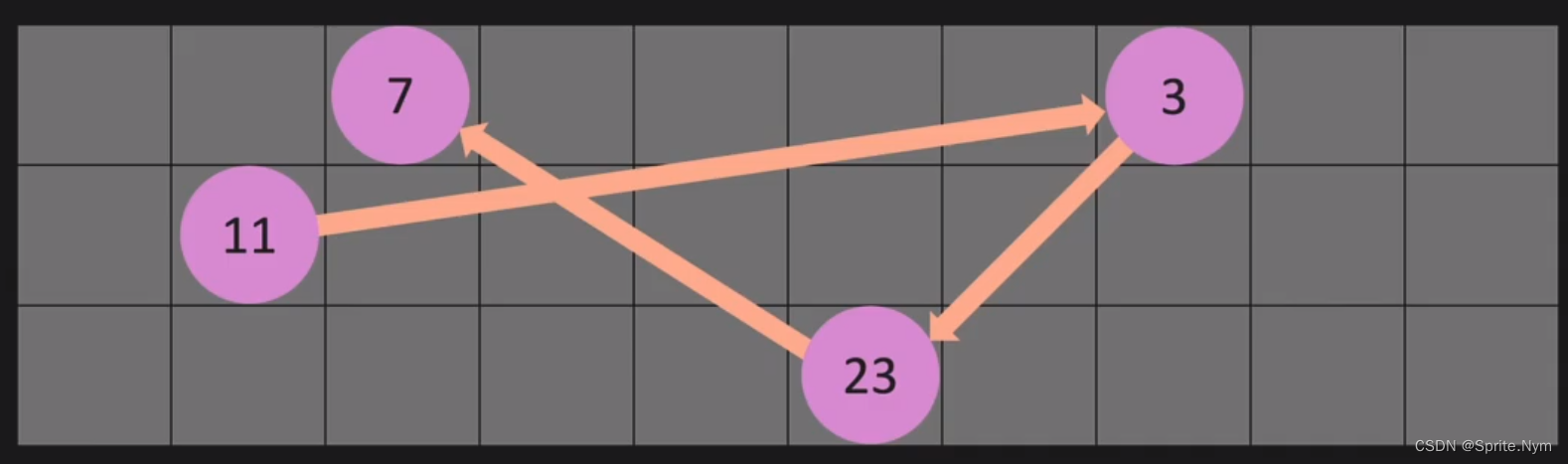
和列表对比下:
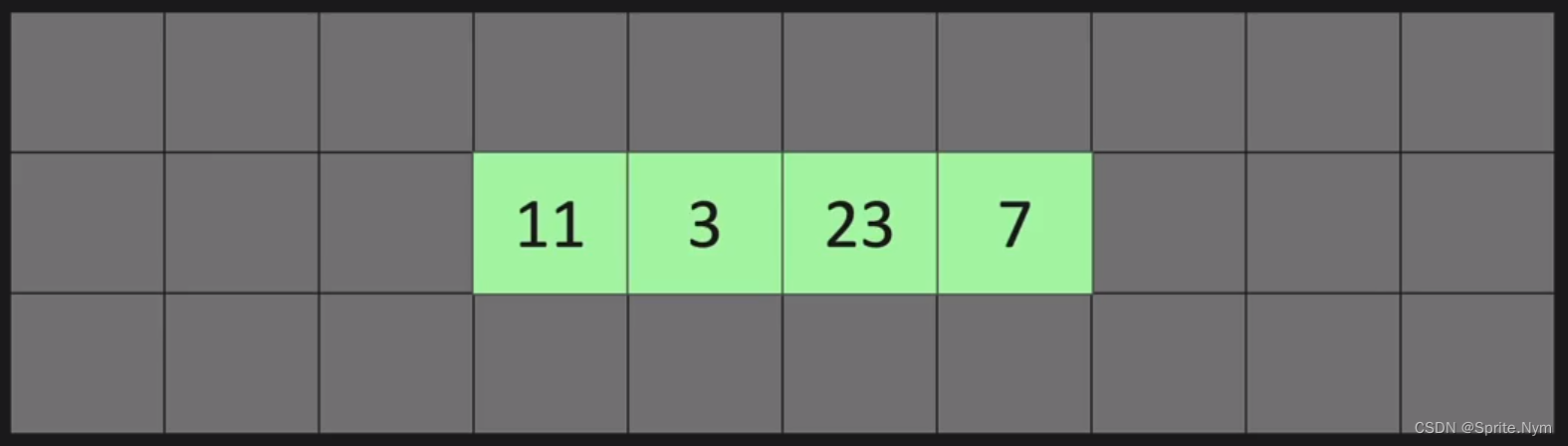
3.2 链表方法的Big O
(1)尾部加入一个节点,时间复杂度为O(1)。因为和前面的节点都无关。
(2)尾部删除一个节点,时间复杂度为O(n)。因为尾部删除节点后,tail必须倒退一个节点,而它没有指向上一个节点的指针,所以必须从头遍历一遍。
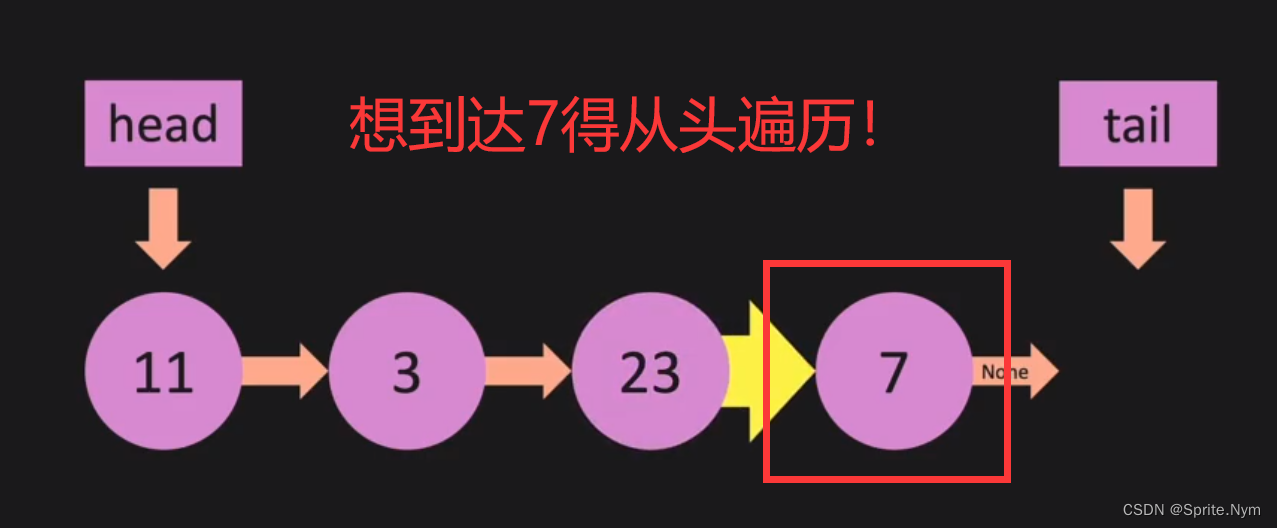
(3)头部加入一个节点,时间复杂度为O(1)。因为和后面的节点都无关。
(4)头部删除一个节点,时间复杂度为O(1)。head先后移一个节点,随后删除原来的头部节点,和后面的节点无关。
(5)中间插入一个节点,时间复杂度为O(n)。先遍历到想插入的位置,新节点指针先复制原来这里节点的指针,以便能指向后一个节点,再改变原节点的指针方向到插入节点上。
(6)中间删除一个节点,时间复杂度为O(n)。原理类似插入,先遍历,再改变指针方向,最后再删除。
(7)查找:不论是按值还是按第n个查找,都得遍历,因此时间复杂度为O(n)。
(8)总结:根据使用场景选择链表or列表。
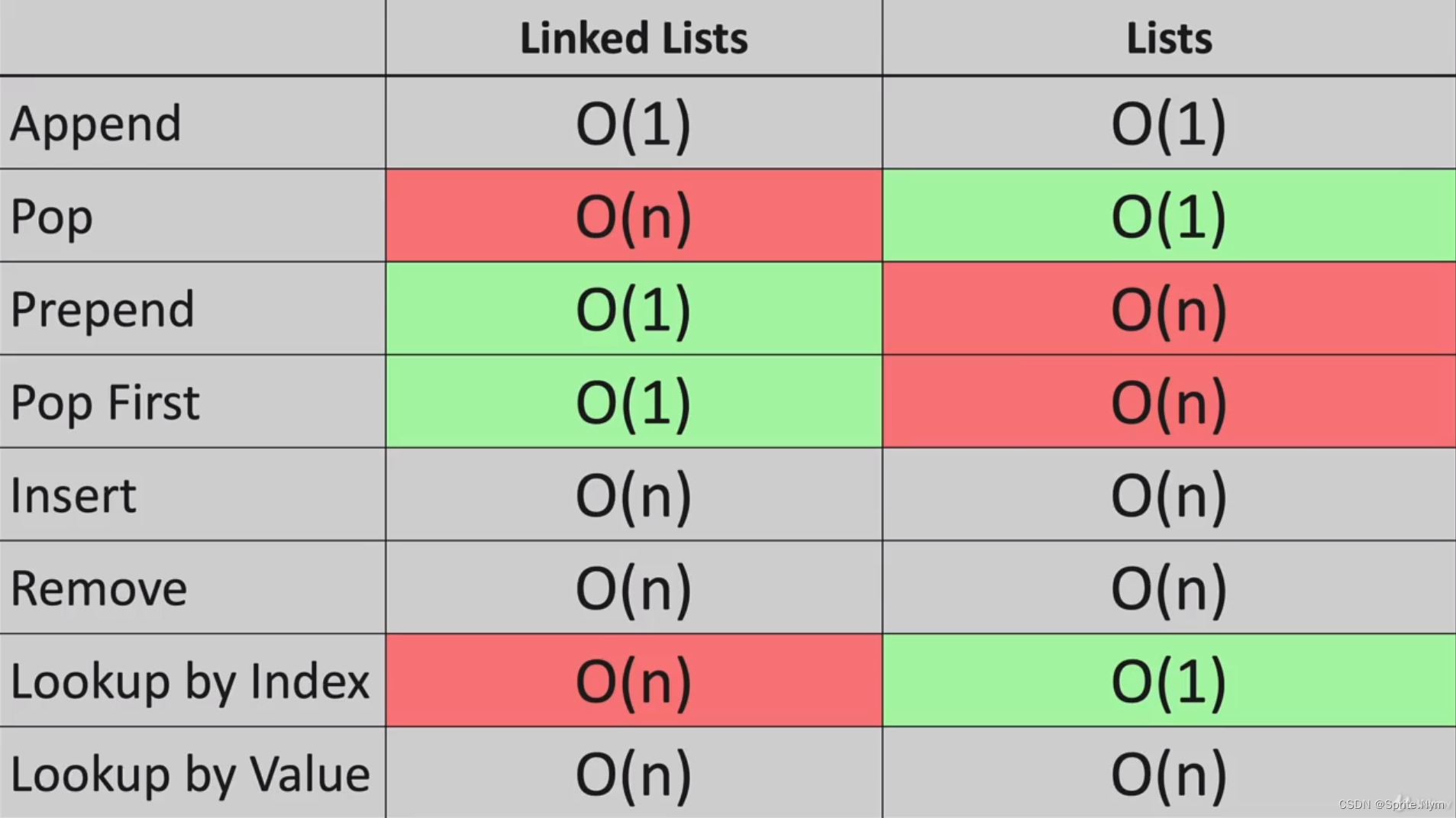
3.3 底层逻辑
(1)节点(Node):值和指针共同组成了节点。本质上相当于一个字典。
{
"value": 4,
"next": None
}
可以暂且当做一个嵌套字典来理解:
在这里插入图片描述
3.4 Constructor
由于链表的append、prepend、insert方法都涉及到创建新节点,为了不让代码重复书写,要单独创建一个节点类。
class Node:
def __init__(self, value):
self.value = value
self.next = None
class LinkedList:
def __init__(self, value):
# 创建新节点
new_node = Node(value)
self.head = new_node
self.tail = new_node
self.length = 1
my_linked_list = LinkedList(4)
3.5 Print
遍历打印。
def print_list(self):
temp = self.head()
while temp:
print(temp.value)
temp = temp.next
3.6 Append
在尾部追加节点。
def append(self, value):
new_node = Node(value)
if self.head:
self.tail.next = new_node
self.tail = new_node
else:
self.head = new_node
self.tail = new_node
self.length += 1
return True
3.7 Pop
原理:设置两个变量temp和pre,都向右遍历,当temp.next == None时,就把pre设置成新的tail,同时返回temp。
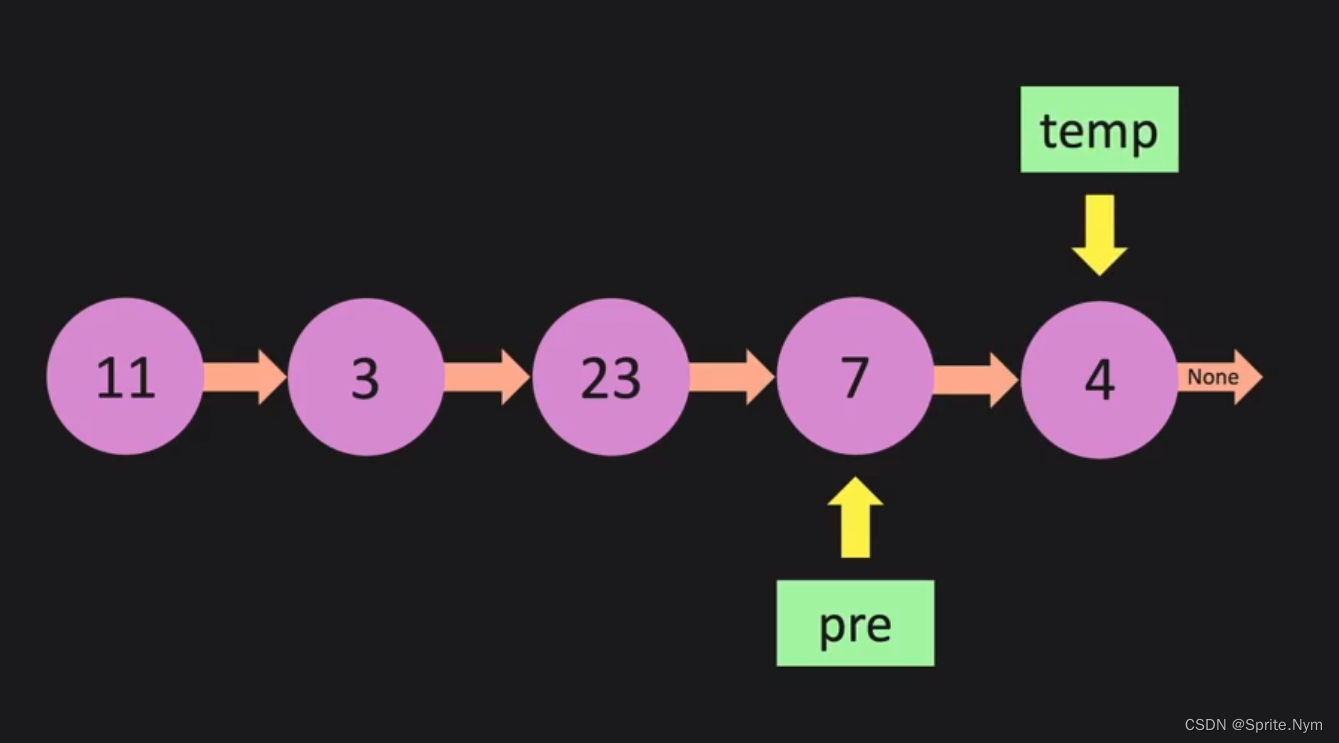
def pop(self):
if self.length == 0:
return None
temp, pre = self.head, self.head
while temp.next:
pre = temp
temp = temp.next
self.tail = pre
self.tail.next = None
self.length -= 1
if self.length == 0:
self.head, self.tail = None, None
return temp
3.8 Prepend
在头部追加节点。
def prepend(self, value):
new_node = Node(value)
if self.length == 0:
self.head = new_node
self.tail = new_node
else:
new_node.next = self.head
self.head = new_node
self.length += 1
return True
3.9 Pop First
提取出第一个节点。
def pop_first(self):
if self.length == 0:
return None
temp = self.head
self.head = self.head.next
temp.next = None
self.length -= 1
if self.length == 0:
self.tail = None
return temp
3.10 Get
返回第index个节点。
def get(self, index):
if index < 0 or index >= self.length:
return None
temp = self.head
for _ in range(index):
temp = temp.next
return temp
3.11 Set Value
更改链表第index个节点的值。
def set_value(self, index, value):
temp = self.get(index)
if temp:
temp.value = value
return True
return False
3.12 Insert
在链表第index个节点处插入新节点。
def insert(self, index, value):
if index < 0 or index > self.length:
return False
if index == 0:
return self.prepend(value)
if index == self.length:
return self.append(value)
new_node = Node(value)
temp = self.get(index-1)
new_node.next = temp.text
temp.next = new_node
return True
3.13 Remove
删除链表第index个节点,并返回该节点。
def remove(self, index):
if index < 0 or index > self.length:
return False
if index == 0:
return self.pop_first()
if index == self.length:
return self.pop()
prev = self.get(index-1)
temp = prev.next
prev.next = temp.next
temp.next = None
self.length -= 1
return temp
3.14 Reverse
反转链表。
def reverse(self):
temp = self.head
self.head = self.tail
self.tail = temp
before = None
for _ in range(self.length):
after = temp.next
temp.next = before
before = temp
temp = after
四、双向链表
4.1 Constructor
跟单向的区别就是节点多了个prev属性。
class Node:
def __init__(self, value):
self.value = value
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self, value):
new_node = Node(value)
self.head, self.tail = new_node, new_node
self.length = 1
4.2 Append
跟单向的区别就是新节点加进来后prev属性为之前的tail。
def append(self, value):
new_node = Node(value)
if self.head is None:
self.head, self.tail = new_node, new_node
else:
self.tail.next = new_node
new_node.prev = self.tail
self.tail = new_node
self.length += 1
return True
4.3 Pop
跟单向链表的区别是不用遍历了!
def pop(self):
if self.length == 0:
return None
temp = self.tail
if self.length == 1:
self.head, self.tail = None, None
else:
self.tail = temp.prev
self.tail.next, temp.prev = None, None
self.length -= 1
return temp
4.4 Prepend
跟单向链表的区别是要多设置一个prev属性为新节点。
def prepend(self, value):
new_node = Node(value)
if self.head is None:
self.head, self.tail = new_node, new_node
else:
new_node.next = self.head
self.head.prev = new_node
self.head = new_node
self.length += 1
return True
4.5 Pop First
跟单向链表的区别是最后要设置头节点的prev属性为None。
def pop_first(self):
if self.length == 0:
return None
temp = self.head
if self.length == 1:
self.head, self.tail = None, None
else:
self.head = temp.next
self.head.prev, temp.next = None, None
self.length -= 1
return temp
4.6 Get
跟单向链表的区别是多了个判断语句,如果要找的点在整个链表的左半部分,就从头部遍历,反之从尾部遍历。
def get(self, index):
if index < 0 or index >= self.length:
return None
if index < self.length / 2:
temp = self.head
for _ in range(index):
temp = temp.next
else:
temp = self.tail
for _ in range(self.length - 1, index, -1):
temp = temp.prev
return temp
4.7 Set Value
跟单向链表的代码没有区别,但是get方法的执行有区别。
def set_value(self, index, value):
temp = self.get(index)
if temp:
temp.value = value
return True
return False
4.8 Insert
跟单向链表的区别是要设置prev属性。
def insert(self, index, value):
if index < 0 or index > self.length:
return False
if index == 0:
return self.prepend(value)
if index == self.length:
return self.append(value)
new_node = Node(value)
before = self.get(index-1)
after = before.next
new_node.next, new_node.prev = after, before
before.next, after.prev = new_node, new_node
self.length += 1
return True
4.9 Remove
跟单向链表的区别是要设置prev属性。
def remove(self, index):
if index < 0 or index >= self.length:
return None
if index == 0:
return self.pop_first()
if index == self.length - 1:
return self.pop()
temp = self.get(index)
before = temp.prev
after = temp.next
before.next, after.prev = after, before
temp.next, temp.prev = None, None
self.length -= 1
return temp
五、栈
5.1 简介
(1)LIFO:Last In First Out。每次放入一个新元素,它之前那个元素就取不到了。最后进去的最先取到。

(2)应用:
浏览器的“上一步”按钮,每按一次会回到上一个页面

(3)构造栈:
- 列表型的栈:每次加入新元素时就append,取出时就pop。两者的时间复杂度都是O(1)。

- 单向链表型的栈:每次要加入时就prepend,取出时就pop_first。两者的时间复杂度都是O(1)。如果从尾部,时间复杂度就会变成O(1)和O(n),更复杂。
5.2 Constructor
类似单向链表,但不需要尾部(底部)属性,因为栈的加入/取出操作都不涉及底部。
class Node:
def __init__(self, value):
self.value = value
self.next = None
class Stack:
def __init__(self, value):
new_node = Node(value)
self.top = new_node
self.height = 1
def print_stack(self):
temp = self.top
while temp:
print(temp.value)
temp = temp.next
5.3 Push
def push(self, value):
new_node = Node(value)
if self.height == 0:
self.top = new_node
else:
new_node.next = self.top
self.top = new_node
self.height += 1
return True
5.4 Pop
def pop(self):
if self.top == 0:
return None
temp = self.top
self.top = temp.next
temp.next = None
self.height -= 1
return temp
六、队列
6.1 简介
(1)FIFO:First In First Out。像排队一样,先进先出。进称为Enqueue,出称为Dequeue。
(2)构造队列:
- 列表型队列:在头部加入元素时间复杂度为O(n),在尾部取出元素时间复杂度为O(1)。
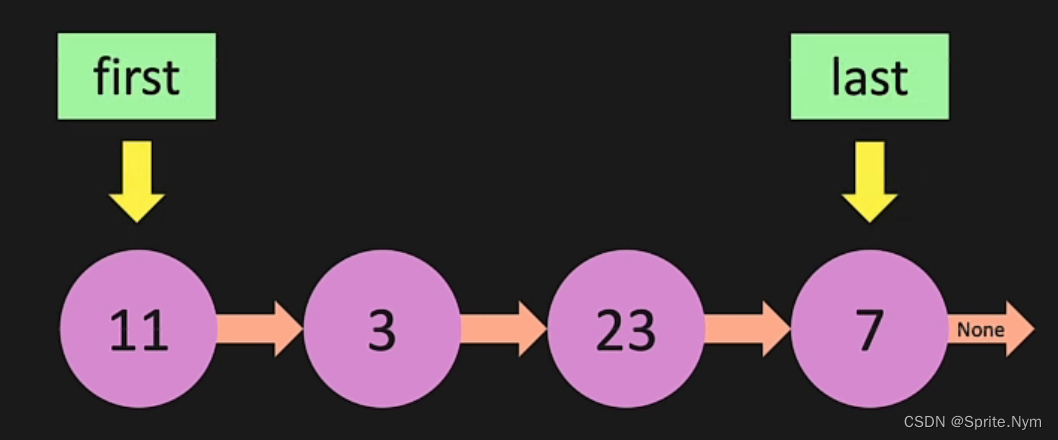
- 链表型队列:在尾部加入元素时间复杂度为O(1),在头部取出元素时间复杂度为O(1)。
6.2 Constructor
和单向链表类似。
class Node:
def __init__(self, value):
self.value = value
self.next = None
class Queue:
def __init__(self, value):
new_node = Node(value)
self.first, self.last = new_node, new_node
self.length = 1
def print_queue(self):
temp = self.first
while temp:
print(temp.value)
temp = temp.next
6.3 Enqueue
和append类似。
def enqueue(self, value):
new_node = Node(value)
if self.first is None:
self.first, self.last = new_node, new_node
else:
self.last.next = new_node
self.last = new_node
self.length += 1
return True
6.4 Dequeue
和pop_first类似。
def dequeue(self):
if self.length == 0:
return None
temp = self.first
if self.length == 1:
self.first, self.last = None, None
else:
self.first = temp.next
temp.next = None
self.length -= 1
return temp
七、二叉树
7.1 树的简介
(1)单向链表可以看做不分叉的树,即树的特例。
(2)树的结构:

同样可以当做字典去理解:

(3)术语:
- Full:如果一个二叉树上的所有节点都要么指向0个节点,要么指向两个节点,就是Full的。
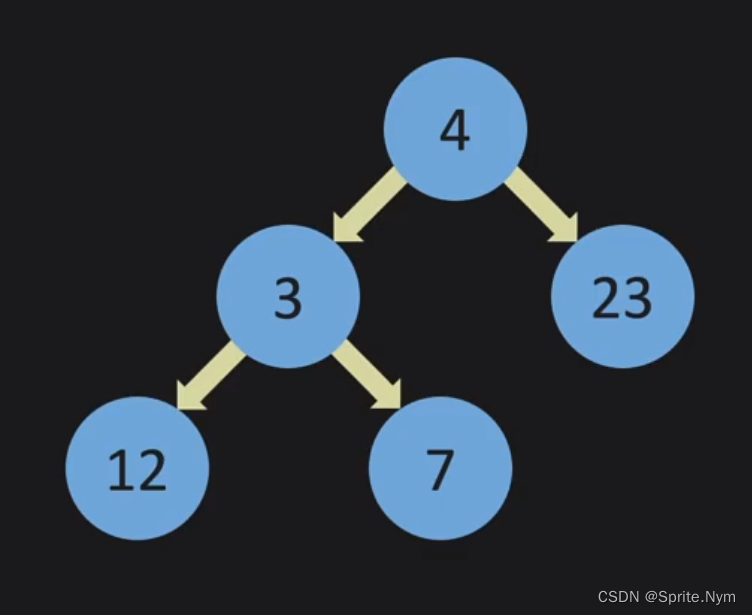
现在7指向2,所以不Full了。
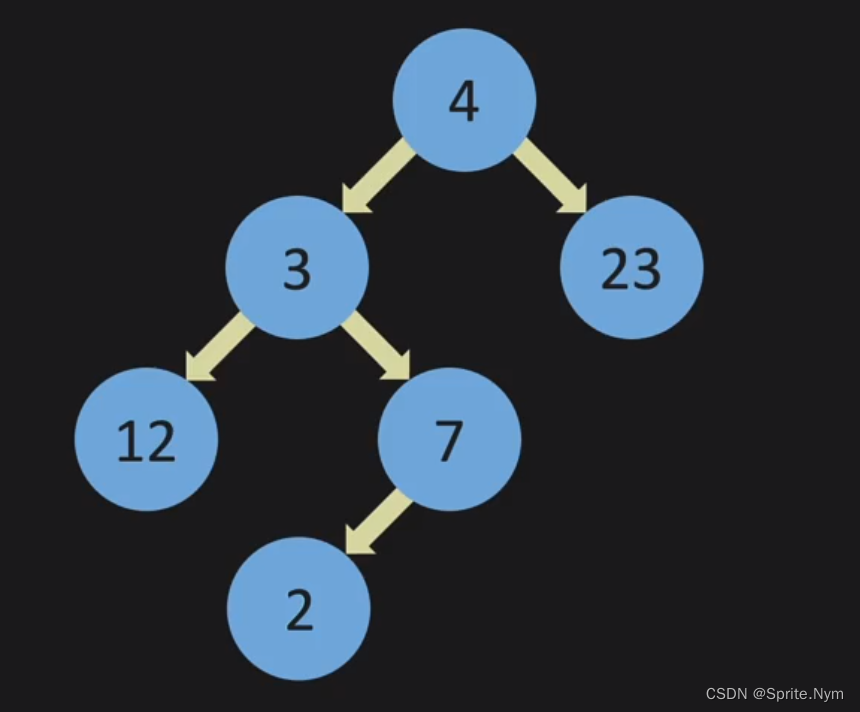
- Perfect:每一层的每个节点都有全部分叉。
现在右边没有分叉,不Perfect了:
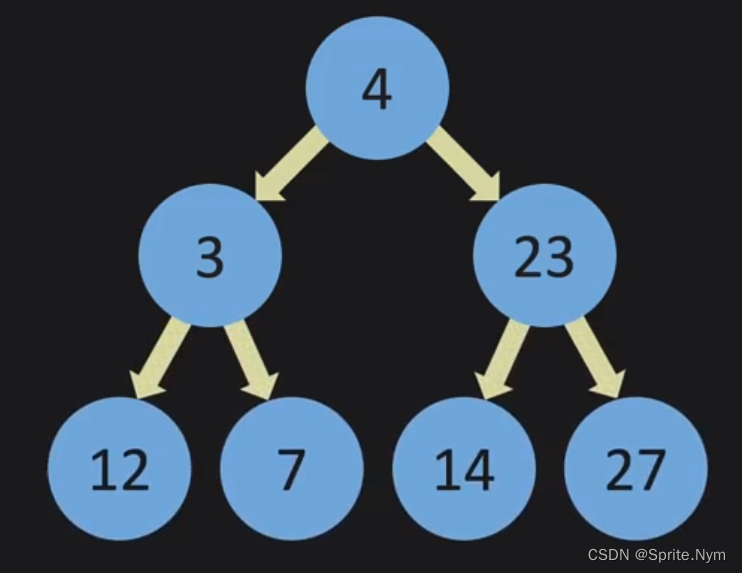
- Complete:如果一棵树是从左到右填充的,就是Complete的。
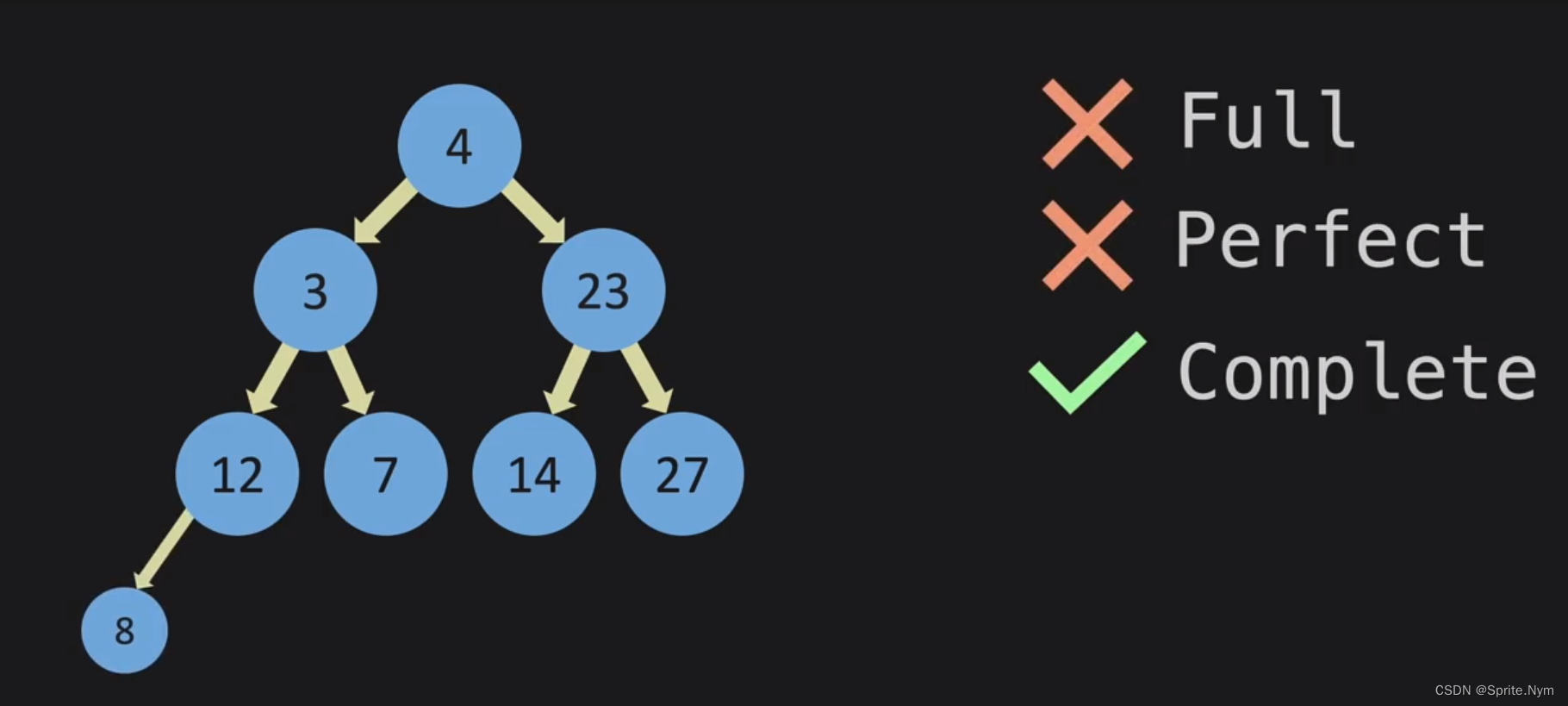
- Parent、Child、Sibling:任何节点的上一个节点就是它的父节点,它自己就是这个父节点的子节点。具有相同父节点的两个子节点称为Siblings。
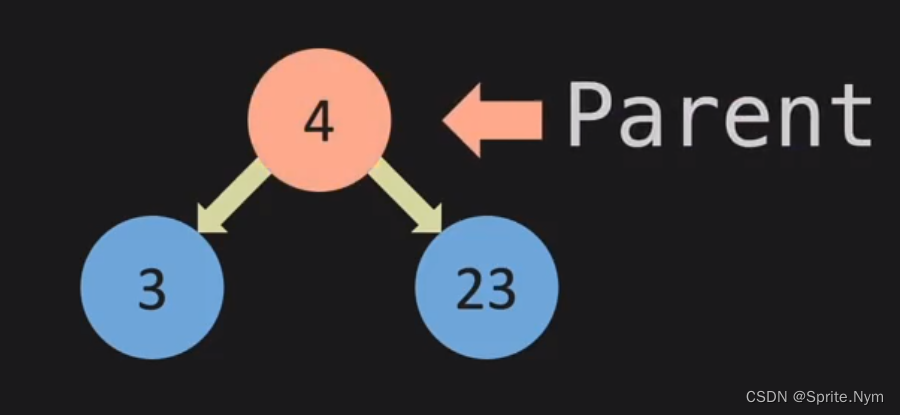
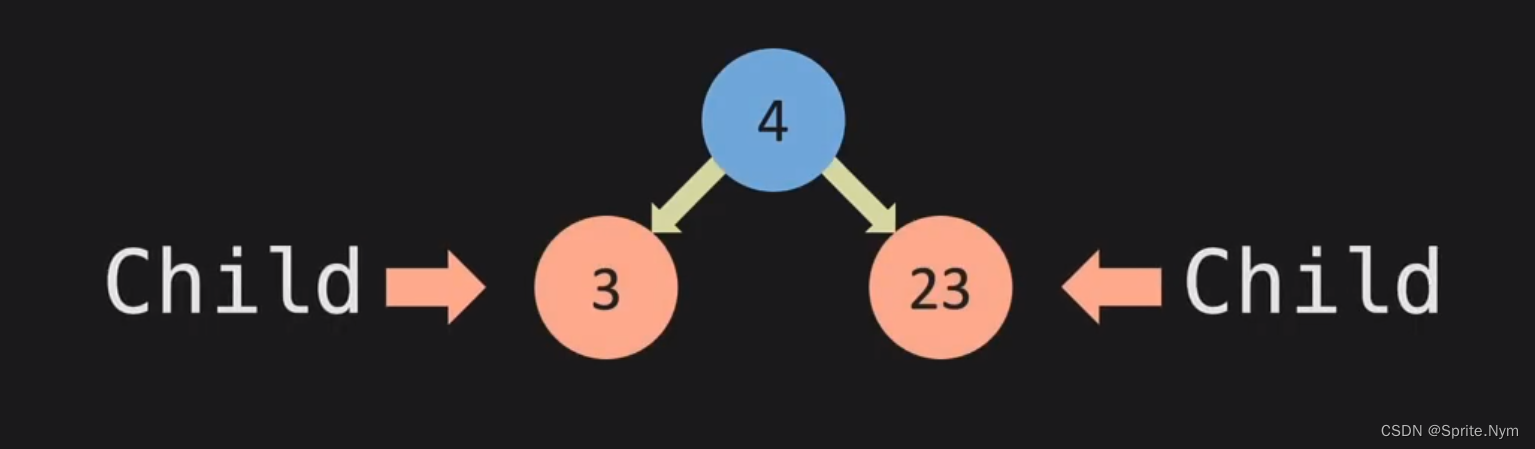
- Leaf:完全没有子节点的节点叫做Leaf,叶节点。
7.2 二叉查找树(BST)简介
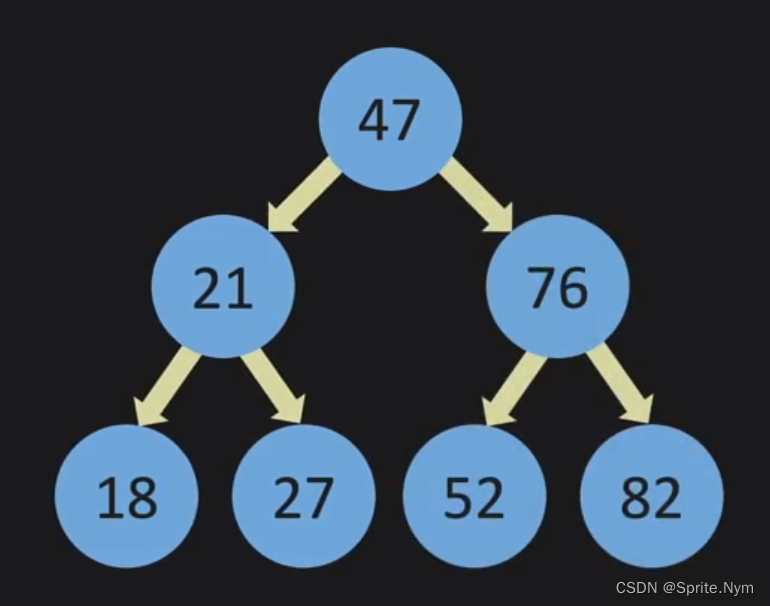
第一个值作为根节点,往后每放进来一个值,就与根节点比较大小。
如果比根节点小,就放在左边,反之放在右边。
之后的节点除了与根节点比较,还要与第二层、第三层的节点比较大小,直到它成为当前二叉树的一个叶节点。
7.3 BST的Big O
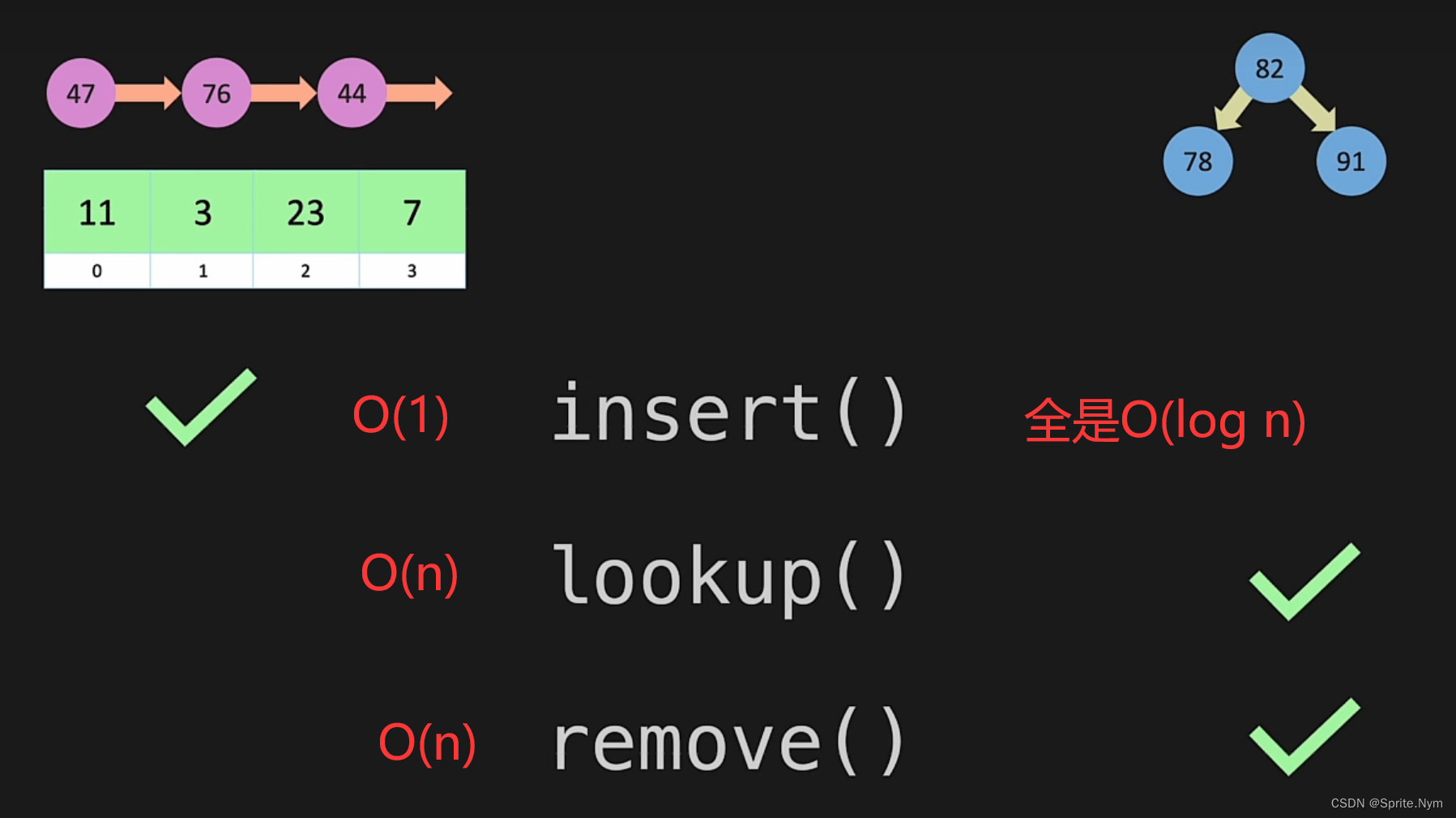
Perfect二叉树的节点总个数可以用等比数列求和公式计算,即n层二叉树的节点个数为 2 n ? 1 2^n-1 2n?1。
简单起见约等于 2 n 2^n 2n,在这样的二叉树中,想要搜索到某个值,或者删除、加入某个值,一共需要经过n次判断,所以时间复杂度为O(log n)。O(log n)的思想就是分治法。
下图为链表和列表与二叉搜索树的时间复杂度比较。
7.4 Constructor
和前面的数据结构有个区别:第一个节点(即根节点)不传value,不实例化Node对象,为None。之后再用insert加节点。
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
7.5 Insert
思路:每次想加入一个新节点,就从根节点开始创建一个临时变量,比较临时变量和新节点的大小,比较完后临时变量进入树的下一层,被赋予新的值,继续和新节点比较大小。反复如此,直到临时变量抵达树的最后一层。特例是,如果原来是空树,就直接把新节点设置成根节点,如果新节点和原有节点重复了,就直接返回False。
def insert(self, value):
new_node = Node(value)
if self.root is None:
self.root = new_node
return True
temp = self.root
while True:
if temp.value == new_node.value:
return False
if temp.value > new_node.value:
if temp.left is None:
temp.left = new_node
return True
temp = temp.left
else:
if temp.right is None:
temp.right = new_node
return True
temp = temp.right
7.6 Contain
用一个temp变量从根节点开始在树中查找,如果目标值比temp小,temp就被赋予原先左边的值,反之右边的值,一直到temp和目标相等为止,就返回True。如果没找到就返回False。
def contains(self, value):
temp = self.root
while temp is not None:
if value < temp.value:
temp = temp.left
elif value > temp.value:
temp = temp.right
else:
return True
return False
八、哈希表
8.1 哈希表简介
(1)简介:类似一个字典、一个商店,每种不同的东西都被有条不紊地存在不同的地方,这样要取用时就可以直接去对应的地址找。
(2)特点:
- 单向的(ONE WAY):只能由Key通过哈希函数计算出地址,而不能反过来由地址计算出Key。
- 确定的(Deterministic):每一个Key都能计算出它专属的独一无二的地址。
(3)查找:每当想根据Key查找Value,都可以计算出Key对应的地址,然后直接从这个地址取出Value。
8.2 Collisions
(1)哈希冲突:当同一个地址存了多个键值对,就发生了哈希冲突。
(2)分离链接法(Separate Chaining):将这些键值对都存在一个大列表中。类似的,也可以存成链表。
(3)线性探测法(Linear Probing)(open addressing的一种):后来的值顺着内存往下找,直到找到一个空的内存地址,就存放在这里。
本课程处理哈希冲突的方式是合并为大列表。
8.3 Constructor
思路:先开辟一个指定size的空列表,列表中每个元素都为None。然后写一个哈希函数,这里使用除留余数法。
class HashTable:
def __init__(self, size = 7):
self.data_map = [None] * size
def __hash(self, key):
my_hash = 0
for letter in key:
my_hash = (my_hash + ord(letter) * 23) % len(self.data_map)
return my_hash
def print_table(self):
for i, val in enumerate(self.data_map):
print(i, ':', val)
8.4 Set
每次想加入一个新键值对时先用哈希函数计算index,然后放入index对应地址。如果该地址为空,则先创建一个列表再append键值对,否则直接append键值对。
def set_item(self, key, value):
index = self.__hash(key)
if not self.data_map[index]:
self.data_map[index] = []
self.data_map[index].append([key, value])
8.5 Get
先根据键,用哈希函数计算出地址,再去地址遍历查找。
def get_item(self, key):
index = self.__hash(key)
if self.data_map[index]:
for item in self.data_map[index]:
if item[0] == key:
return item[1]
return None
8.6 Keys
遍历data_map,再遍历每个地址的每个键值对,取出所有键。
def keys(self):
all_keys = []
for data in self.data_map:
if data:
for item in data:
all_keys.append(item[0])
return all_keys
8.7 Big O
由于在实际哈希表中,哈希冲突相当罕见,键值对基本是平均分布在表中。所以对于任何操作,都只有使用哈希函数计算地址这一个操作,时间复杂度为O(1)。
8.8 常见面试题
两个列表中是否有相同元素:
(1)方法一:天真解法:嵌套循环,遍历比较,时间复杂度为O(n2)。
(2)方法二:遍历第一个列表时把列表中的元素全部加入一个字典,值都设为True。遍历第二个列表时检查元素是否在之前的字典中。只走两个循环,时间复杂度为O(2n),简化表示为O(n)。
九、图
9.1 图的简介
(1)Vertex(复数Vertices)和Edge:Vertex类似前面数据结构中节点。Edge是各个Vertex之间的联结。
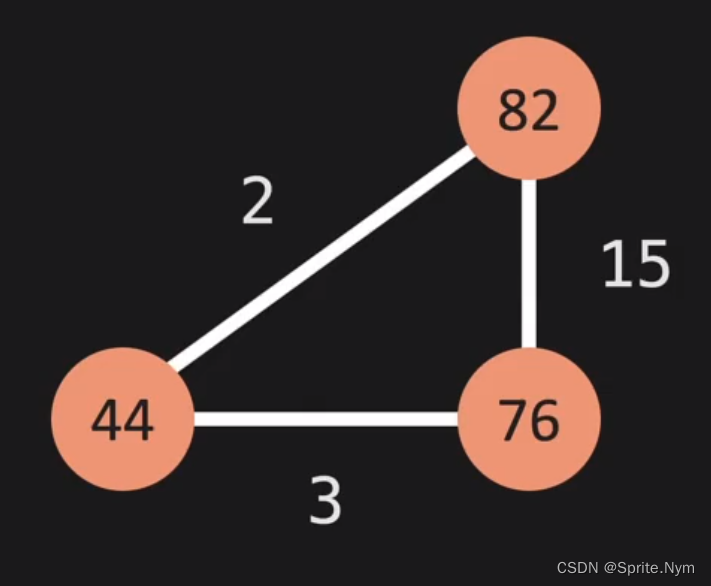
下图为一个图的案例,红色点为Vertices,白线为Edge,白线上的值称为权重,带权重的Edge称为Weighted Edge。
地图就是图的典型应用(Weighted Edge),比如下图中,如果不加权,从76到82就选择直接走上去,但是假设考虑到塞车(加权),则会选择先从76带44,再去82。
社交应用的社交网也是图,互关的人,Edge是双向的,例如某人和她朋友。而某人和她关注的网红则是单向Edge。
总结:Edge可以是加权或不加劝,可以是双向,或单向。
树可以看做是图的特殊形式。
9.2 Adjacency Matrix
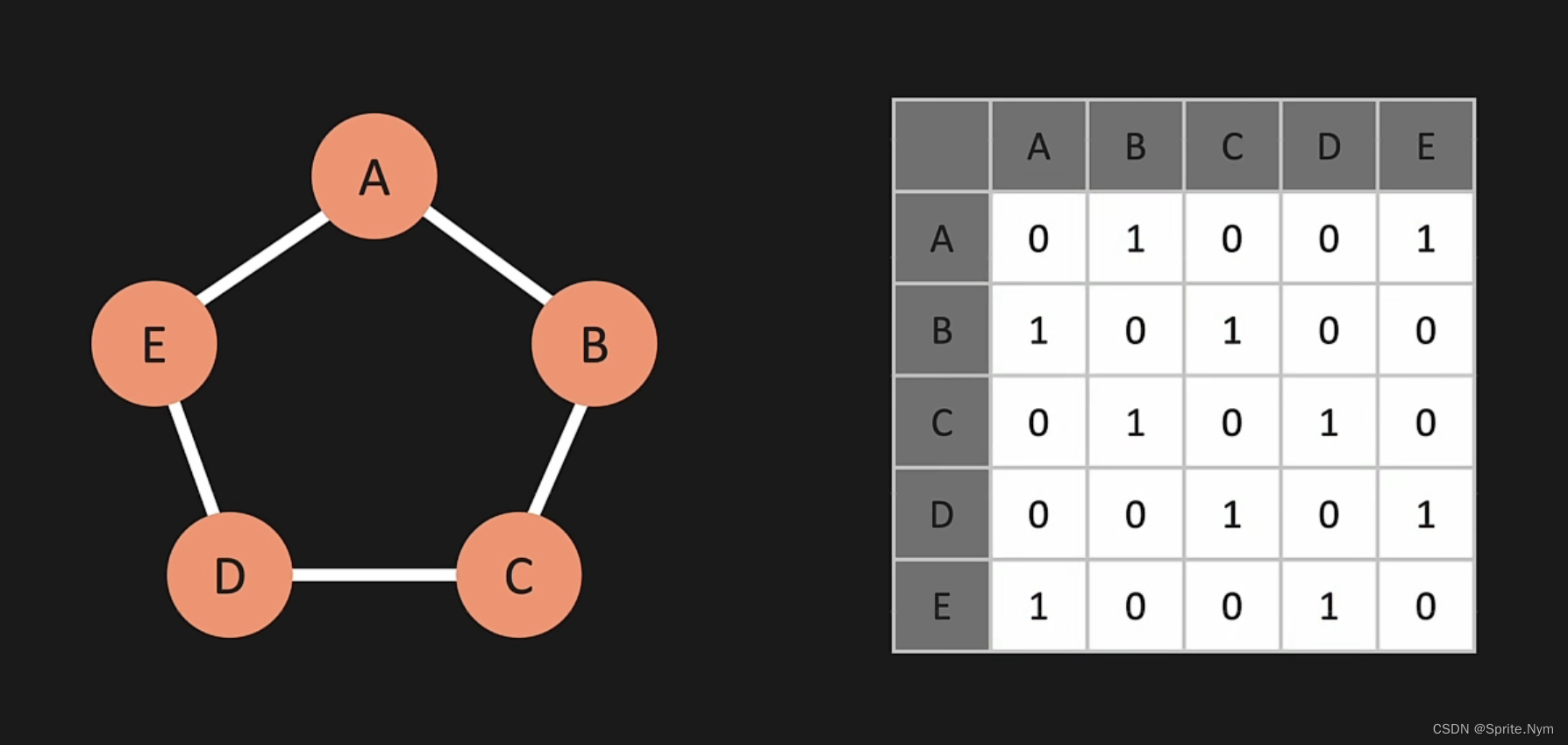
邻接矩阵(Adjacency Matrix)是图的一种表示方式。
每个行i与每个列j对应的点,表示从i到j的Edge(注意是i到j,有方向的)。
如果图中的Edge都是双向的,则整个邻接矩阵沿着AA、BB、CC、DD、EE这条对角线对称。
如果图中的Edge是单向的,则可想原本应该对称的两个点,会变成一个0,一个1。
如果Edge带权重,则把邻接矩阵中的1替换成应有的权重。
9.3 Adjacency List
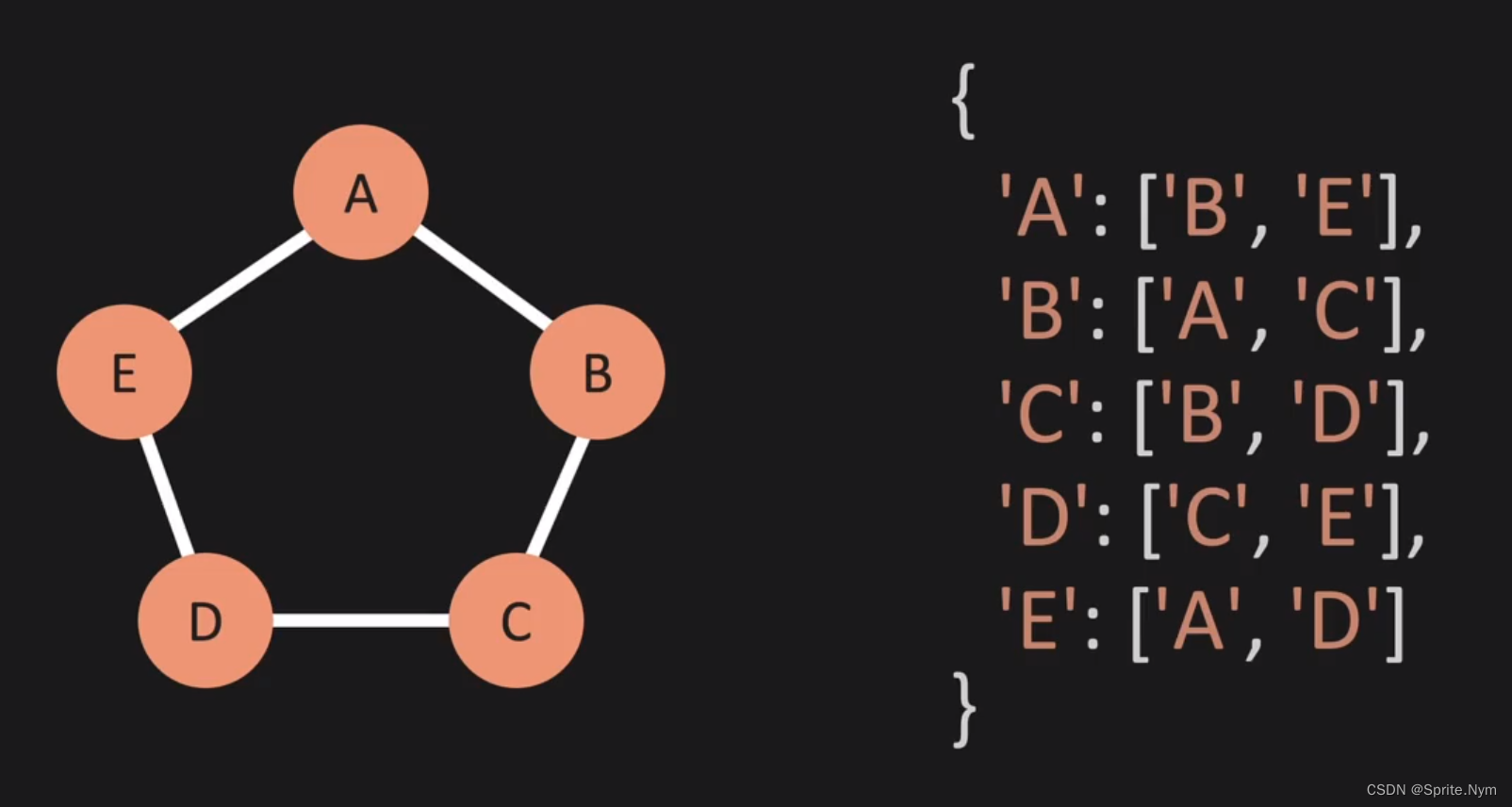
邻接表(Adjacency List)是图的另一种表示方式。
9.4 图的Big O
(1)空间复杂度:

(2)加入新Vertex的时间复杂度, 差异巨大:

(3)加入新Edge的时间复杂度,均为O(1):

(4)删除Edge,矩阵可以直接定位到对应Edge,而表基本得把Edge遍历一次:

(5)删除Vertex,矩阵要删除行和列,表要遍历一遍,删除目标Vertex和其他Vertex中有关联的Edge。

总结:由于邻接矩阵中0过多,浪费了太多空间,在数据量极大时,占用的空间也会非常大,并不是一种很好的选择。所以本课程使用邻接表。
9.5 Add Vertex
初始的图对象带有一个空字典,每次加入Vertex就新建一个键值对,键就是Vertex,值是空列表,准备之后存Edge。这个方法需要先检测是否该Vertex已存在于图中。
class Graph:
def __init__(self):
self.adj_list = {}
def print_graph(self):
for vertex in self.adj_list:
print(vertex, ':', self.adj_list[vertex])
def add_vertex(self, vertex):
if vertex not in self.adj_list.keys():
self.adj_list[vertex] = []
return True
return False
9.6 Add Edge
给定两个Vertex,v1和v2,添加它们的Edge。注意,下面写的这个方法只能加入双向无权重Edge。
def add_edge(self, v1, v2):
if v1 in self.adj_list.keys() and v2 in self.adj_list.keys():
self.adj_list[v1].append(v2)
self.adj_list[v2].append(v1)
return True
return False
9.7 Remove Edge
基本和add edge一样。
def remove_edge(self, v1, v2):
if v1 in self.adj_list.keys() and v2 in self.adj_list.keys():
self.adj_list[v1].remove(v2)
self.adj_list[v2].remove(v1)
return True
return False
9.8 Remove Vertex
def remove_vertex(self, vertex):
if vertex in self.adj_list.keys():
for other_vertex in self.adj_list[vertex]:
self.adj_list[other_vertex].remove(vertex)
del self.adj_list[vertex]
return True
return False
十、递归
10.1 递归的简介
(1)定义:递归就是一个调用自身的函数,直到无法再调用。
(2)用开礼物盒举例。每次开箱,如果是球,就返回球,否则再次调用开箱函数。伪代码如下
def open_gift_box():
if ball:
return ball
open_gift_box()
注意两点:
- 每次开箱的过程都是相同的。
- 每次开箱,都使问题更小了。
(3)概念:上面例子中的“球”被称为“Base Case”,即递归停止情况;“箱”被称为“Recursive Case”,即递归情况。
注意:
- Base Case必须要可以为True,否则就陷入死循环。
- Base Case下面必须要跟return语句,否则执行完Base Case下的语句,仍然会继续递归,还是会陷入死循环。
10.2 非递归函数如何调用栈
假设现在有三个函数:函数1调用函数2,然后打印1、函数2调用函数3,然后打印2、函数3直接打印3。
那么他们在栈中的顺序应该是函数1先进去,然后函数2进去,最后是函数3进去。
但是由于1要等2执行,2要等3执行。所以最先打印出来的是3,然后函数3就执行完了,接着就被移出栈。接着打印2,然后函数2被移出栈,最后是1。

10.3 递归函数如何调用栈
以阶乘为例。
def own_fact(n):
if n == 1:
return 1
return n * own_fact(n - 1)

十一、冒泡排序、选择排序和插入排序
11.1 冒泡排序简介
每一次循环都两两比较,小的数放左边,大的数放右边,一次循环结束后,最大的数就会到最右边。n个数共经历n-1次循环后就排好了。每次循环需要比较的次数都会-1,因为之前的循环已经把右边的数排好了,不需要再比较了。
11.2 冒泡排序代码
比普通的冒泡排序多了一个检测:设置一个检测是否排好序的变量is_ok,每次循环都初始化为True,如果发生了顺序交换,就改为False。如果某次循环中,一次顺序交换都没有发生,则is_ok保持为True,说明已经排好序了,之后也不用再循环了,直接break。
此外排序完成后的列表是一个新列表,不改动原列表。
def bubble_sort(my_list):
result = my_list.copy()
for i in range(len(result) - 1, 0, -1):
is_ok = True
for j in range(i):
if result[j] > result[j + 1]:
result[j], result[j + 1] = result[j + 1], result[j]
is_ok = False
if is_ok:
break
return result
11.3 选择排序
从左往右遍历,每次遍历都找到最小值的index,然后将最左边的(未排好序)的值和最小值根据index交换位置。注意每次循环只需要做一次交换。第一轮循环结束,index为0的值必然是最小值,第二轮从index为1开始遍历,以此类推。
11.4 选择排序代码
def selection_sort(my_list):
result = my_list.copy()
for i in range(len(result) - 1):
min_index = i
for j in range(i + 1, len(result)):
if result[j] < result[min_index]:
min_index = j
# 只有当min_index发生改变时,才需要把最小值换过来
if i != min_index:
result[i], result[min_index] = result[min_index], result[i]
return result
11.5 插入排序简介
从左往右循环。第一次循环从第二个数开始,每次和它左边的每个数依次比较,如果比左边的数更小,就交换位置。
11.6 插入排序代码
def insertion_sort2(my_list):
result = my_list.copy()
for i in range(1, len(result)):
temp = my_list[i]
j = i - 1
while temp < result[j] and j > -1:
result[j + 1], result[j] = result[j], temp
j -= 1
return result
11.7 插入排序的Big O
完全乱序的数组,会执行双重循环,时间复杂度为O(n2)。
几乎排好序的数组,基本只用执行外层循环,内层循环只会偶尔执行,时间复杂度为O(n)。
十二、归并排序、快速排序
12.1 归并排序概述
先将一个数组不断二分,直到每个子数组只剩下单个元素。然后顺着分割路径合并,只不过这次合并时要进行排序。比如原来[2、1]被分成了[2]和[1],合并时就合并成[1、2]。一直合并直到重新成为一个整体。
12.2 Merge部分简介
这里只介绍归并部分,并非排序的完整过程。假设前面的合并都已完成(贪心),即现在的两个列表内部已经排好序。
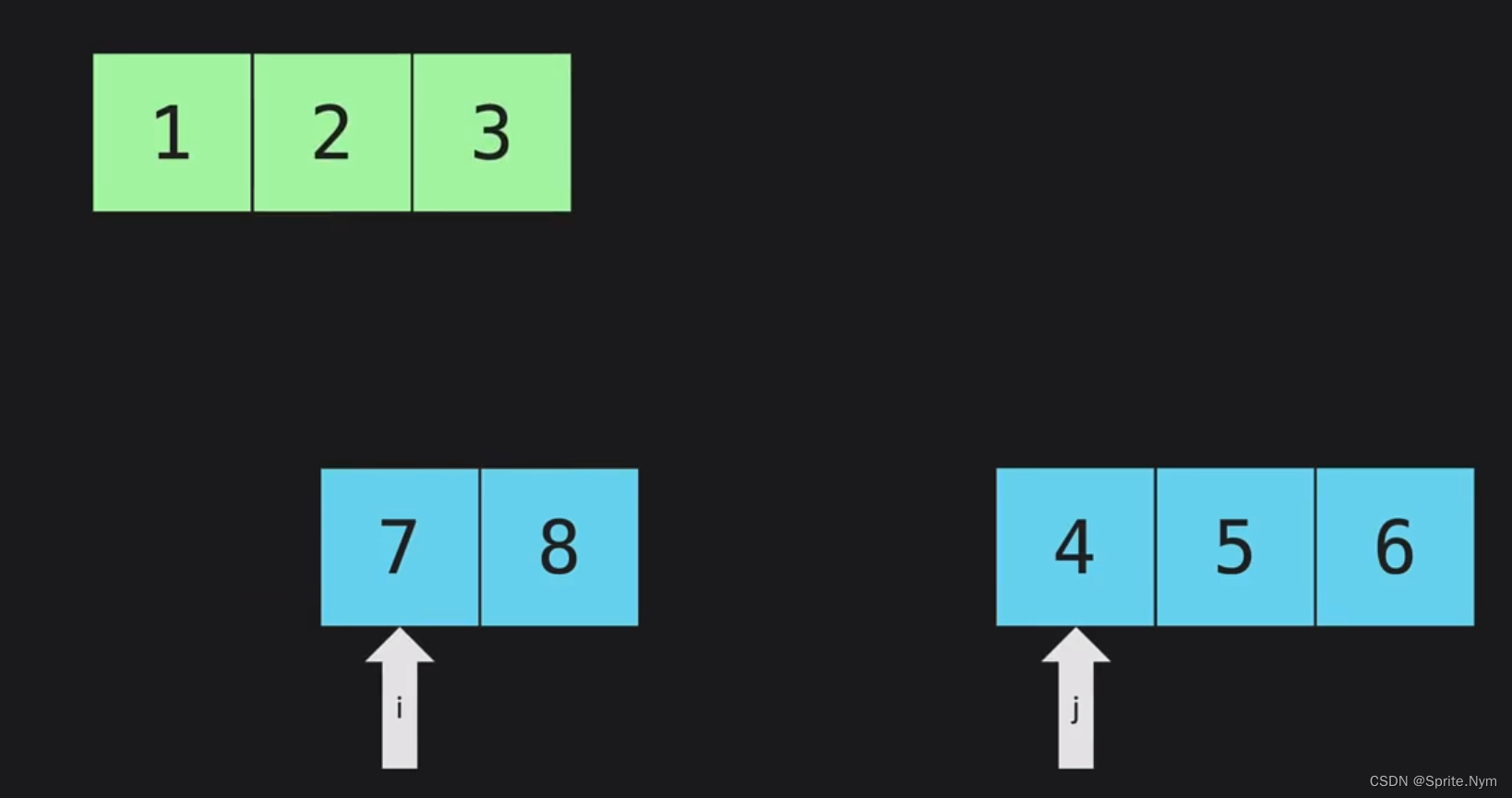
用两个变量i和j作为索引分别来代表两个列表的元素,哪个变量小,就把它加入结果列表中,同时它的索引+1。一直重复,直到某个列表被遍历完,此时再把另一个列表中剩下的元素全部加到结果列表中。
12.3 Merge部分代码
def merge(list1, list2):
combined = []
i = 0
j = 0
n = len(list1)
m = len(list2)
while i < n and j < m:
if list1[i] < list2[j]:
combined.append(list1[i])
i += 1
else:
combined.append(list2[j])
j += 1
while i < n:
combined.append(list1[i])
i += 1
while j < n:
combined.append(list2[j])
j += 1
return combined
12.4 归并排序简介
使用递归:
(1)每次递归都要使问题更小:二分切割原列表。
(2)递归需要有Base Case来停止递归:当列表长度切分到1。
(3)最后使用merge()来合并。
12.5 归并排序代码
这里加入了一个功能,可以像Python自带的排序函数一样传一个函数进去,每次比较两个元素大小时,这个函数都会先对这两个元素进行映射(如果不传就不进行映射,保持元素的原样),以保证它们按照指定的规则排序。比如下面代码,列表里是一系列字符串形式的数,排序规则是比较个位的大小。
def merge(list1, list2, f=lambda x: x):
i, j = 0, 0
n, m = len(list1), len(list2)
combined = []
while i < n and j < m:
if f(list1[i]) < f(list2[j]):
combined.append(list1[i])
i += 1
else:
combined.append(list2[j])
j += 1
while i < n:
combined.append(list1[i])
i += 1
while j < m:
combined.append(list2[j])
j += 1
return combined
def merge_sort(my_list, f=lambda x: x):
if len(my_list) == 1:
return my_list
mid = len(my_list) // 2
left = my_list[:mid]
right = my_list[mid:]
return merge(merge_sort(left, f), merge_sort(right, f), f)
l1 = [str(random.randint(1, 100)) for _ in range(100)]
print(merge_sort(l1, f=lambda x: x[-1]))
"""
测试结果:
['50', '100', '10', '40', '100', '60', '60', '40', '60', '30', '70', '90', '90', '71', '21', '31', '21', '81', '31', '31', '62', '82', '82', '22', '22', '82', '52', '62', '72', '92', '52', '82', '92', '52', '53', '83', '73', '73', '53', '73', '33', '43', '64', '4', '74', '54', '34', '74', '94', '4', '5', '75', '65', '15', '95', '25', '55', '6', '96', '6', '6', '96', '26', '6', '26', '96', '96', '66', '36', '26', '36', '17', '57', '47', '7', '97', '27', '97', '87', '77', '68', '28', '88', '68', '98', '98', '98', '68', '88', '89', '89', '79', '19', '89', '49', '89', '79', '99', '79', '39']
"""
12.6 归并排序的Big O
(1)空间复杂度:O(n)。之前的排序可以copy()并将结果存在新列表中,也可以就地排序。但归并排序是不得不创建新列表排序,占用空间是列表原空间的两倍。
(2)时间复杂度:二分到不可分割的步骤,时间复杂度为O(log n)。重新归并的步骤要遍历列表,时间复杂度为O(n)。乘起来的时间复杂度为O(n log n)。
冒泡排序、选择排序和插入排序的时间复杂度都是O(n2),显然归并排序效率更高。
十三、快速排序
13.1 快速排序简介
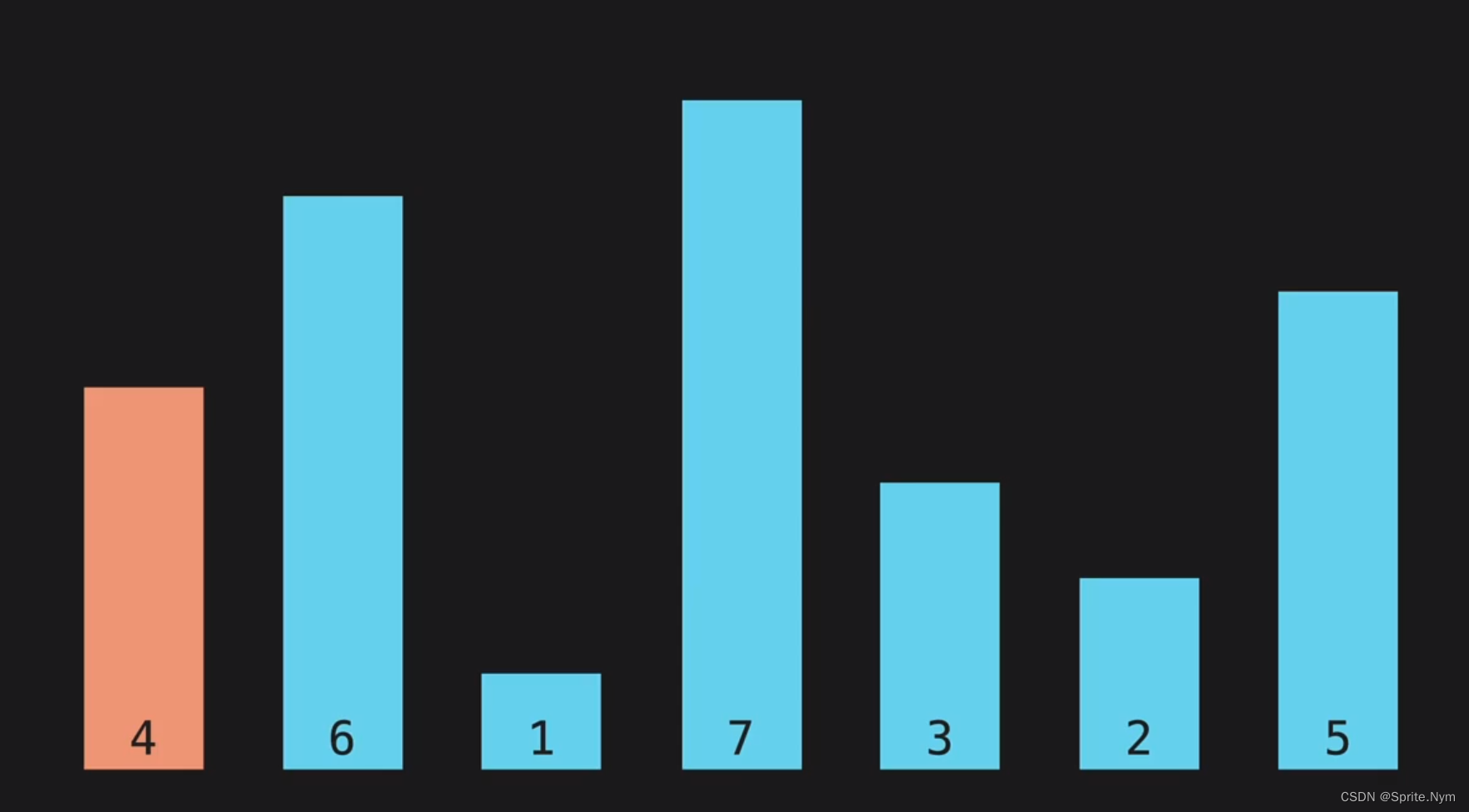
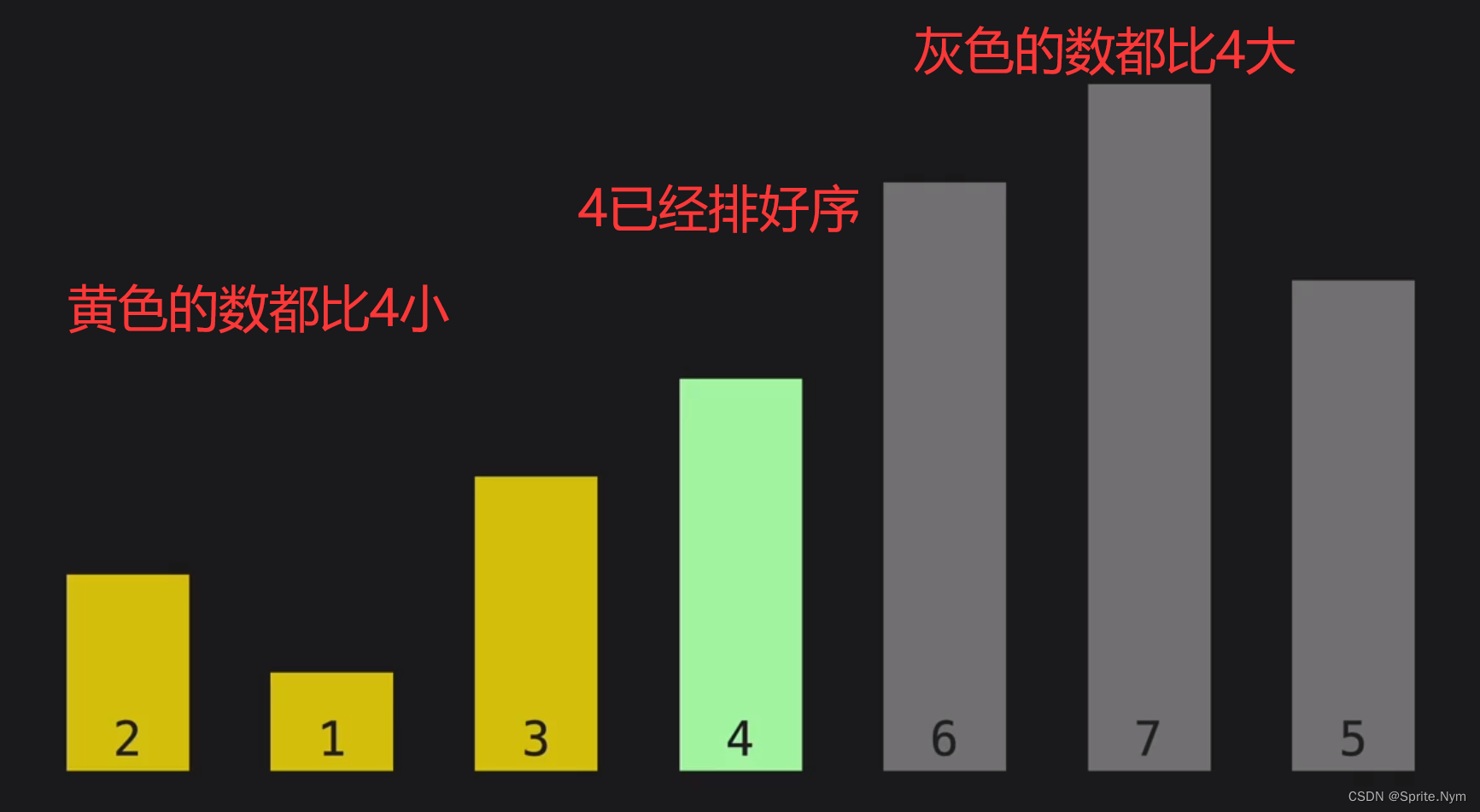
每次选择列表的第一个元素作为基准,然后往后遍历,每当找到比基准数大的数时就继续遍历,每当找到比基准数小的数时,就和首个比基准数大的数交换位置。这样遍历下来,比基准数大的数和比基准数小的数就会完全分开,此时再把基准数和比基准数小的最后一个数交换位置。此时就完成了一轮。完成一轮后,基准数就处在中间,且已经排好序,再对两边的数继续使用快速排序,不断重复即可。
初始:
完成一轮快速排序后:
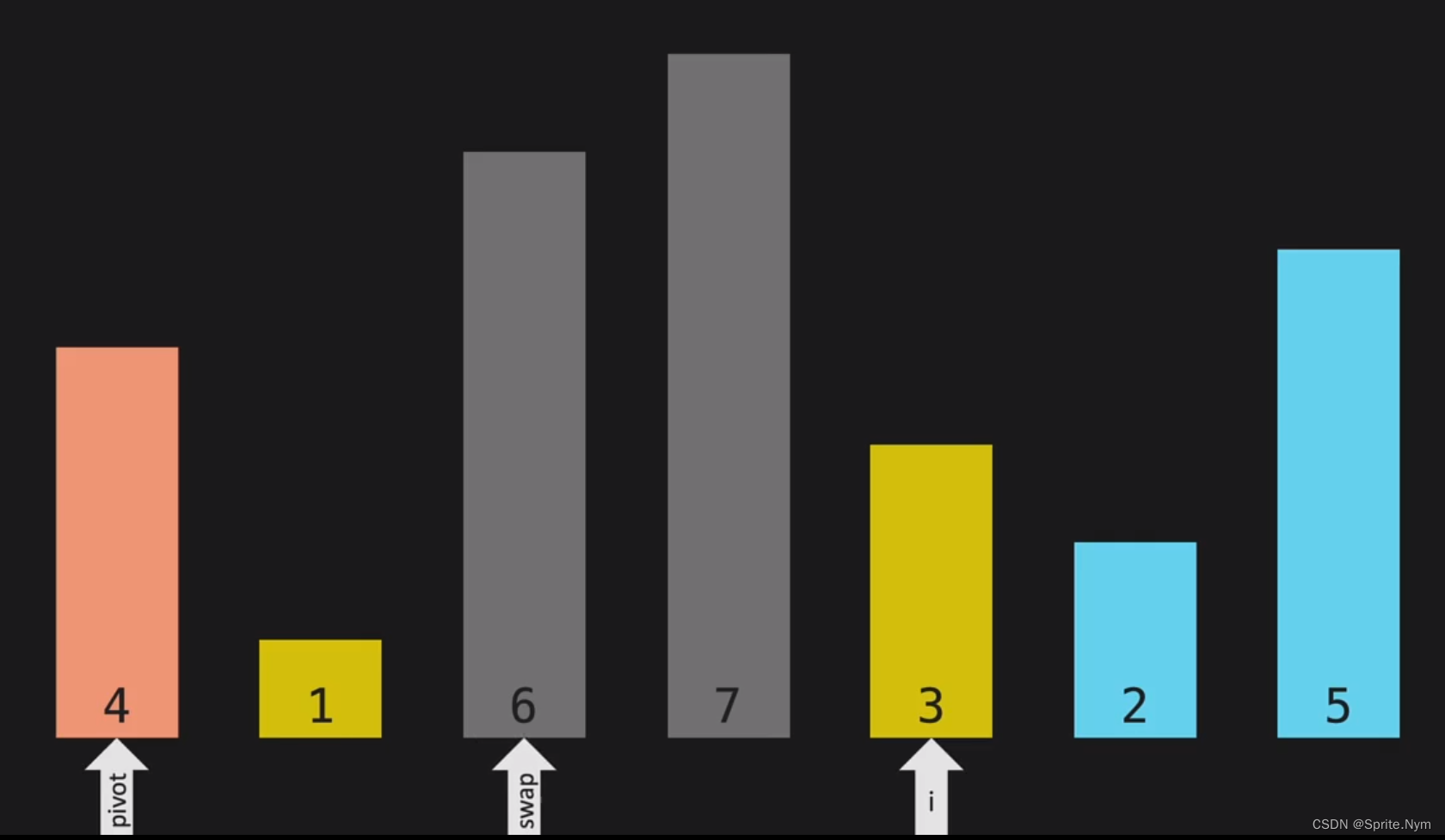
13.2 Pivot部分简介
设置3个指针,Pivot指针标记Pivot Value。i指针负责向后遍历。Swap指针负责交换。每当i指针遇到比Pivot Value大的数时,Swap指针就不动;反之Swap指针前移,并和i指针所指的数交换。i指针遍历结束后,再将Pivot Value和Swap指针所指的数交换。
13.3 Pivot部分代码
注意返回值只有一个中间的索引,这是为了让下次快速排序找到列表的切分点。
def pivot(my_list, pivot_index, end_index):
swap_index = pivot_index
for i in range(pivot_index + 1, end_index + 1):
if my_list[i] < my_list[pivot_index]:
swap_index += 1
my_list[swap_index], my_list[i] = my_list[i], my_list[swap_index]
my_list[pivot_index], my_list[swap_index] = my_list[swap_index], my_list[pivot_index]
return swap_index
13.4 快速排序代码
quick_sort_helper函数用于递归,如果传入的左端点小于右端点,则执行递归,否则返回原列表。
quick_sort函数负责计算出右端点,并调用quick_sort_helper部分,这样就不用自己去计算右端点位置了。同样,如果不想改变原列表,只想返回新列表,也可以在quick_sort中copy()一份。
def pivot(my_list, pivot_index, end_index):
swap_index = pivot_index
for i in range(pivot_index + 1, end_index + 1):
if my_list[i] < my_list[pivot_index]:
swap_index += 1
my_list[swap_index], my_list[i] = my_list[i], my_list[swap_index]
my_list[pivot_index], my_list[swap_index] = my_list[swap_index], my_list[pivot_index]
return swap_index
def quick_sort_helper(my_list, left, right):
if left < right:
pivot_index = pivot(my_list, left, right)
quick_sort_helper(my_list, left, pivot_index - 1)
quick_sort_helper(my_list, pivot_index + 1, right)
return my_list
def quick_sort(my_list):
return quick_sort_helper(my_list, 0, len(my_list) - 1)
13.5 快速排序的Big O
运行Pivot函数遍历一遍的时间复杂度是O(n)。
而最好和平均情况是,每次刚好都能让Pivot Value被换到列表中间位置去,刚好能对列表二等分,实现分治。此时的总时间复杂度是O(n log n)。
而最坏的情况是列表已经排好序了,每次的Pivot Value都停在开头,每次递归只是减少了一个元素,无法分治。此时的总时间复杂度为O(n2)。
所以如果已知列表的顺序很乱,可以用快速排序,如果顺序已经比较好了,就使用插入排序。
十四、树遍历
14.1 树遍历简介
(1)先从左到右遍历完一层,再进入下一层继续遍历的方式被称为Breadth First Search,宽度优先搜索。
(2)先遍历到左下角的叶节点,然后倒着回到根节点,再往右遍历到右下角的遍历方式被称为Depth First Search,深度优先搜索。
14.2 BFS简介
先将节点存在queue列表中,然后将它的值存进results,同时将它的left和right节点继续存进queue中,一直重复到queue为空列表,即遍历结束。
注意:queue最好用链表,用列表是因为比较简单,以便专注于BFS本身。
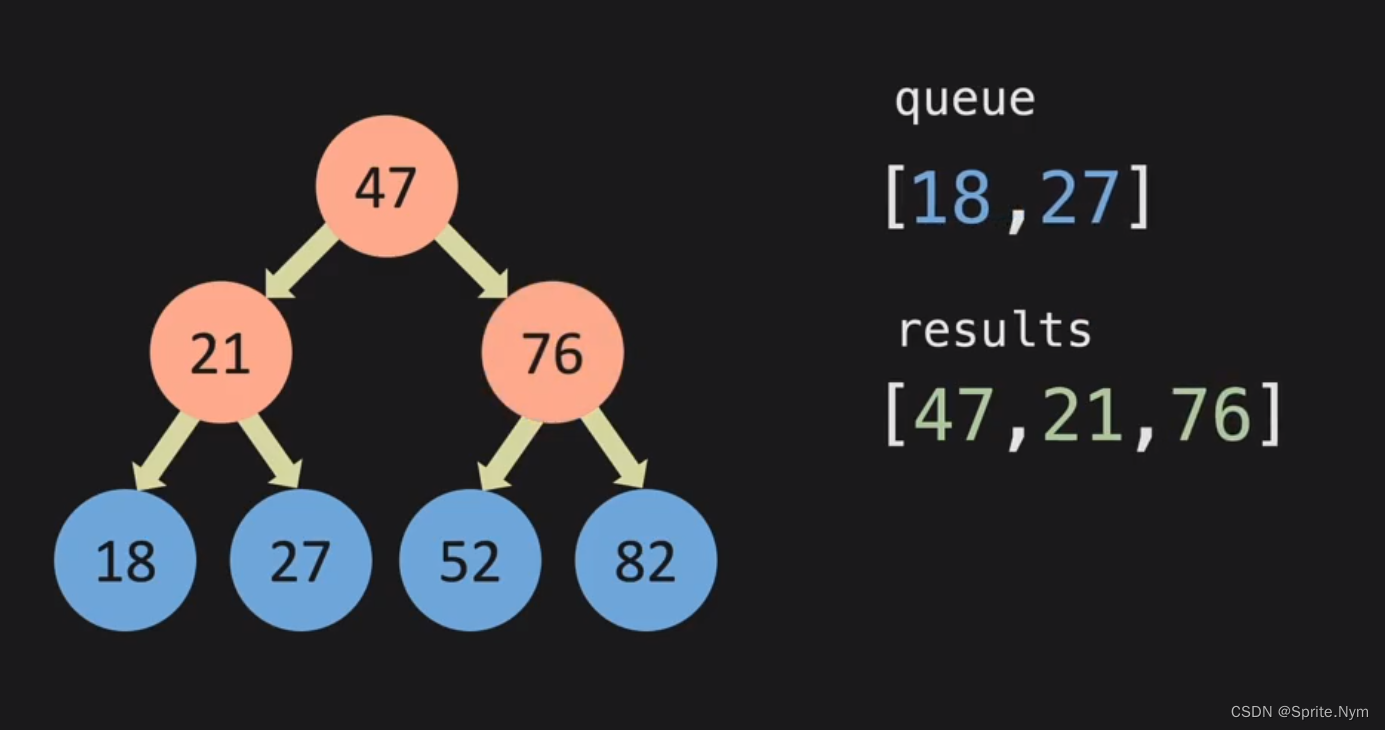
14.3 BFS代码
def BFS(self):
cur_node = self.root
queue = []
results = []
queue.append(cur_node)
while len(queue) > 0:
cur_node = queue.pop(0)
results.append(cur_node.value)
if cur_node.left is not None:
queue.append(cur_node.left)
if cur_node.right is not None:
queue.append(cur_node.right)
return results
14.4 DFS PreOrder简介
先只遍历左边节点直到左下角,再一边倒回根节点一边遍历之前错过的右边的节点,回到根节点时,根节点左边的所有节点被遍历完,然后遍历右边。仍然先遍历左边,再遍历右边。
14.5 DFS代码
用递归实现,由于左边的递归语句在右边前面,所以永远先把左边遍历完了才会开始遍历右边。
def dfs_pre_order(self):
results = []
def traverse(cur_node):
results.append(cur_node.value)
if cur_node.left is not None:
traverse(cur_node.left)
if cur_node.right is not None:
traverse(cur_node.right)
traverse(self.root)
return results
14.6 DFS PostOrder简介
和PreOrder的区别是遍历时先不把某个节点的值写入result中,而是当该节点已经遍历完自己的左右节点了,再将该节点的值写入。这样的效果是越下层的节点值会在result列表的越前面,根节点的值在最后面。
14.7 DFS PostOrder代码
和PreOrder唯一的区别是把result.append()语句放到了递归的下面,所以左右都遍历完了才会加入值。
def dfs_post_order(self):
results = []
def traverse(cur_node):
if cur_node.left is not None:
traverse(cur_node.left)
if cur_node.right is not None:
traverse(cur_node.right)
results.append(cur_node.value)
traverse(self.root)
return results
14.8 DFS InOrder 简介
和PostOrder的区别是append值时不会等到左右节点都遍历完,而是只遍历完左节点就append值,然后再遍历右节点。
14.9 DFS InOrder代码
append写到了中间。
def dfs_in_order(self):
results = []
def traverse(cur_node):
if cur_node.left is not None:
traverse(cur_node.left)
results.append(cur_node.value)
if cur_node.right is not None:
traverse(cur_node.right)
traverse(self.root)
return results