题目

337. 打家劫舍 III【中等】

题解

打家劫舍 I&II&变形系列的新成员，这次房屋的排布变成了树状，还是经典的动态规划问题。
刚开始的想法是树的每一层想成数组的一个元素，相邻层的结点不可以同时选取，即数组的相邻元素不可以同时选取，但是遇到如下的树，
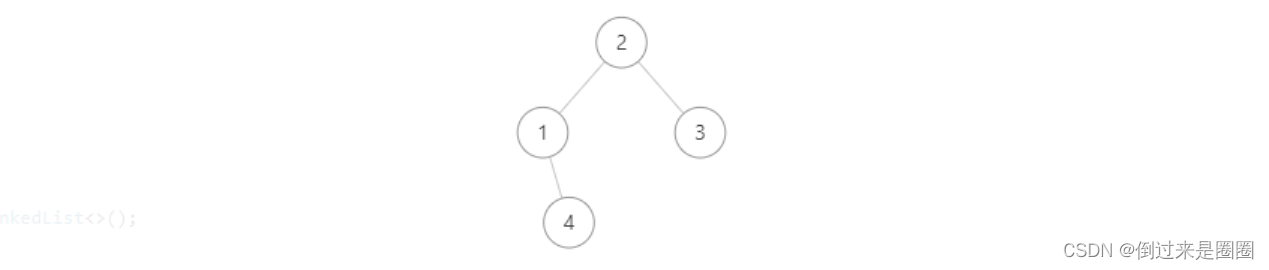
在这里插入图片描述
这种情况的输出是7，即第二层的3结点和第三层的4结点的组合，所以相邻层结点不能同时选取显然是不对的，其实只要不选中有父子关系的结点即可

算法
每一个结点可以设置偷和不偷两种状态，用int[] state=new int[2]来表示，state[0]代表不偷，state[1]代表偷，那么任何结点可以偷到的最大钱数为：

当前结点不偷：当前结点最大钱 = 左子偷到的最大钱 + 右子偷到的最大钱
当前结点偷：当前结点最大钱 = 当前结点值 + 左子自己不偷时能偷到的最大钱 + 右子自己不偷时能偷到的最大钱

公式可以总结为：

root[0] = Math.max(root.left[0],root.left[1]) + Math.max(root.right[0],root.right[1])
root[1] = root.val + root.left[0] + root.right[0]

class Solution {
    public int rob(TreeNode root) {
        int[] res=dfs(root);
        return Math.max(res[0],res[1]);
    }
    public int[] dfs(TreeNode root){
        if(root==null)
            return new int[2];
        int[] state=new int[2];

        int[] left=dfs(root.left);//左子能偷的最大钱
        int[] right=dfs(root.right);//右子能偷的最大钱
        
        state[0]=Math.max(left[0],left[1])+Math.max(right[0],right[1]);//不偷root能得到的最大钱
        state[1]=root.val+left[0]+right[0];//偷root能得到的最大钱
        return state;
    }
}