数据结构

文章目录
前言
初习数据结构,有出错的地方请各位同仁斧正,并希望可以一起探讨交流。本人会持续更新该本教材的精讲和理解,并在不解的地方发起讨论,希望各位大佬能加以解答
一、绪论
1.数据(data)是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
2.数据元素(data element)是数据的基本单位。
3.一个数据元素可由若干个数据项组成,数据项是数据的不可分割的最小单位。
4.数据对象(data object)是性质相同的数据元素的集合,是数据的一个子集。
5.数据结构(data structure)是相互之间存在一种或多种特定关系的数据元素的集合。
思维导图: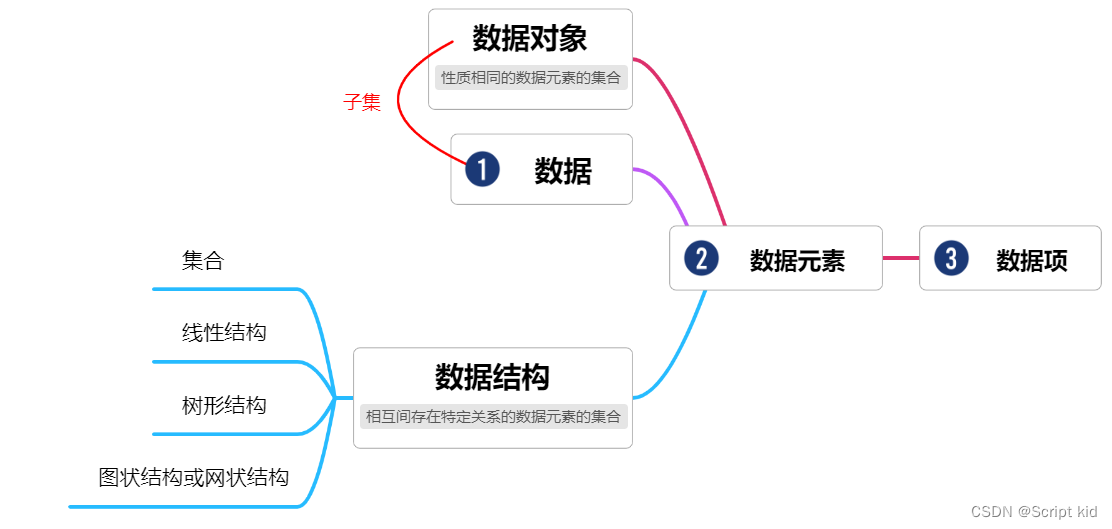
6.数据结构在计算机中的表示(映像)称数据的物理结构,又称存储结构,包括数据元素的表示和关系的表示。(数据的逻辑结构与数据的存储无关)
存储结构由顺序存储结构和链式存储结构两种基本的存储方法实现。
7.逻辑结构:从逻辑关系上描述数据,它与数据的存储无关,是独立于计算机的。因此,数据的逻辑结构可以看作是从具体问题抽象出来的数学模型。
逻辑上可将数据结构分成线性结构和非线性结构。
四种基本关系:集合、线性结构、树形结构、图状结构或网状结构。
一些表面上很不相同的数据可以有相同的逻辑结构。
同一逻辑结构中的所有数据元素具相同的特征,意味着不仅数据元素所包含的数据项的个数要相同,且对应数据项的类型要一致。
树是非线性数据结构,本质是结点的有限集。
8.存储结构是对数据元素内容和个数的体现。
存储实现是对数据元素位置的体现。
运算实现是对数据元素形式上的体现。
逻辑结构理论上,虚拟的东西。
9.数据类型(data type)是一个值的集合和定义在这个值集合上的一组操作的总称。
10.抽象数据类型是应用问题的数学模型及定义在此模型上的一组操作的总称。具体包括三部分:数据对象、数据对象上关系的集合和数据对象的基本操作的集合。
(D,S,P),D是数据对象,S是D上的关系集,P是对D的基本操作集。
11.算法是对特定问题求解步骤的一种描述,是指令的有限序列
12.时间复杂度用大O表示法比较操作数,指出算法运行时间的增速。
O(n),n为操作数。
大O表示法三规则
1.运行时间中所有的加减法常数用常数1代替。
2.只保留最高阶项。
3.去除最高项常数。
二、线性表(n个数据元素的有限序列)
1.抽象数据类型线性表的定义
ADT List{
数据对象:D={ai|∈ElemSet,i=1,2,...,n,n>=0}
数据关系:R1={<ai-1,ai>|ai-1,ai∈D,i=2,...,n}
基本操作:
IntList(&L)
操作结果:构造一个空的线性表L。
DestroyList(&L)
初始条件:线性表L已存在。
操作结果:销毁线性表L。
ClearList(&L)
初始条件:线性表L已存在。
操作结果:将L重置为空表。
ListEmpty(L)
初始条件:线性表L已存在。
操作结果:若L为空表,则返回TRUE,否则返回FALSE。
ListLength(L)
初始条件:线性表L已存在。
操作结果:返回L中数据元素的个数。
GetElem(L,i,&e)
初始条件:线性表L已存在,1<=i<=ListLength(L)
操作结果:用e返回L中第i个数据元素的值。
LocateElem(L,e,compare())
初始条件:线性表L已存在,compare()是数据元素判定函数。
操作结果:返回L中第1个与e满足关系compare()的数据元素的位序。若这样的数据元素不存在,则返回0。
PriorElem(L,cure_e,&pre_e)
初始条件:线性表L已存在。
操作结果:若cur_e是L的数据元素,且不是最后一个,则用pre_e返回它的前驱,否则操作失败,pre_e无定义。
NextElem(L,cur_e,&next_e)
初始条件:线性表L已存在。
若cur_e是L的数据元素,且不是最后一个,则用next_e返回它的前驱,否则操作失败,next_e无定义
ListInsert(&L,i,e)
初始条件:线性表L已存在,1<=i<=LinstLength(L)+1。
操作结果:在L中第i个位置**之前**插入新的数据元素e,L的长度加1。
ListDelete(&L,i,&e)
初始条件:线性表L已存在且非空,1<=i<=ListLength(L)。
操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1。
ListTRaveerse(L,visit())
初始条件:线性表L已存在。
操作结果:依次对L的每个数据元素调用函数visit()。一旦visit()失败,则操作失败。
}ADT List
2. 链表与数组
1.内存
需要将数据存储到内存时,你请求计算机提供存储空间,计算机给你一个存储地址。需要存储多项数据时,有两种基本方式——数组和链表。
2.数组
数组意味着所有数据在内存中都是相连的(紧靠在一起的)。
这便意味着我们想要插入数据就要在计算机中重新开空间,将原数据转移进去,这便造成了时间上的浪费。
或者为了不重开空间,往往会将原定计划的计算机内存空间额外请求扩大位置,若是额外请求的位置可能根本用不上,这将浪费内存,空间浪费。
3.链表
链表中的元素可存储在内存的任何地方,链表的每个元素都存储了下一个元素的地址。
所以链表不能直接访问最后一个数据,需要先访问第一个元素获取第二个元素位置,再不断往下访问递推,因此同时读取所有元素时,链表的效率很高,但如果你需要跳跃,链表的效率真的很低。
4.数组和链表的应用环境
数组适用于对数据的读取(随机访问),而链表只能顺序访问,链表更适合数据的插入,所以一个程序往往要数组与链表的相结合才能更高效。
3.线性表的插入和删除
1.插入
在第i(1<=i<=n)个元素之前插入一个元素时,需将第n至第i个(共n-i+1)个元素向后移动一个位置。
Status ListInsert_Sq(SqList &L,int i,ElemType e){
//在顺序线性表L中第i个位置之前插入新的元素e,
//i的合法值为1<=i<=ListLength_Sq(L)+1
if(i<1||i>L.length+1) return ERROR;//i值不合法
if(L.length>=L.listsize){ //当前存储空间已满,增加分配
newbase=(ElemType*)realloc(L.elem,L.listsize+LISTINCREMENT)*sizeof(ElemType));
if(!newbase)exit(OVERFLOW);//存储分配失败
L.elem=newbase;//新基址
L.listsize +=LISTINCREMENT;//增加存储容量
}
q=&(L.elem[i-1]);//q为插入位置
for(p=&(L.elem[L.length-1]));p>=q;--p)*(p+1)=*p;
//插入位置及之后的元素右移
*q=e;//插入e
++L.length;//表长增1
return OK;
}//ListInsert_Sq
2.删除
删除第i(1<=i<=n)个元素时需将从第i+1至第n个(共n-i)个元素依次向前移动一个位置。
Status ListDelete_Sq(SqList &L,int i,ElemType &e){
//在顺序线性表L中删除第i个元素,并用e值返回其值
i的合法值为1<=i<=ListLength_Sq(L)
if(i<1||i>L.length) return ERROR;//i值不合法
p=&(L.elem+L.length-1);//p为被删除元素的位置
e=*p;//将被删除元素的值赋给e
q=L.elem+L.length-1;//表尾元素的位置
for(++p;p<=q;++p)*(p-1)=*p//被删除元素之后的元素左移
--L.length;//表长减1
return OK;
}//ListDelete_Sq
4.顺序表的合并
void MergeList_Sq(SqList La,SqList Lb,SqList &Lc){
//已知顺序线性表La和Lb的元素按值非递减排列
//归并La和Lb得到新的顺序线性表Lc,Lc的元素也按值非递减排列
pa=La.elem; pb=Lb.elem;
Lc.listsize=Lc.length=La.length+Lb.length;
pc=Lc.elem=(ElemType*)malloc(Lc.listsize*sizeof(ElemType));
if(!Lc.elem)exeit(OVERFLOW);//存储分配失败 //此三行生成C数组
pa_last=La.elem+La.length-1;
pb_last=Lb.elem+Lb.length-1;
while(pa<=pa_last&&pb<=pb_last){ //归并
if(*pa<=*pb)*pc++=*pa++;
else *pc++=*pb++;
}
while(pa<=pa_last)*pc++=*pa++; //插入La的剩余元素
while(pb<=pb_last)*pc++=*pb++; //插入Lb的剩余元素
} //MergeList_Sq