开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 哈希表（Hash table） -> 正文阅读

[数据结构与算法]哈希表（Hash table）

Hash table

哈希表的原理
- 哈希函数
- 冲突解决
[705. 设计哈希集合](https://leetcode.cn/problems/design-hashset/)
- 拉链法
- - 1、定长拉链数组
  - 2、不定长拉链数组
[706. 设计哈希映射](https://leetcode.cn/problems/design-hashmap/)
[217. 存在重复元素](https://leetcode.cn/problems/contains-duplicate/)
[136. 只出现一次的数字](https://leetcode.cn/problems/single-number/)
[349. 两个数组的交集](https://leetcode.cn/problems/intersection-of-two-arrays/)
[202. 快乐数](https://leetcode.cn/problems/happy-number/)

哈希表是一种使用哈希函数组织数据，以支持快速插入和搜索的数据结构。

有两种不同类型的哈希表：哈希集合和哈希映射。

哈希集合是集合数据结构的实现之一，用于存储非重复值。
哈希映射是映射数据结构的实现之一，用于存储(key, value)键值对。

《算法第4版》的散列表章节（293页）

哈希表的原理

哈希表的关键思想是使用哈希函数将键映射到存储桶。更确切地说，

当我们插入一个新的键时，哈希函数将决定该键应该分配到哪个桶中，并将该键存储在相应的桶中；
当我们想要搜索一个键时，哈希表将使用相同的哈希函数来查找对应的桶，并只在特定的桶中进行搜索。

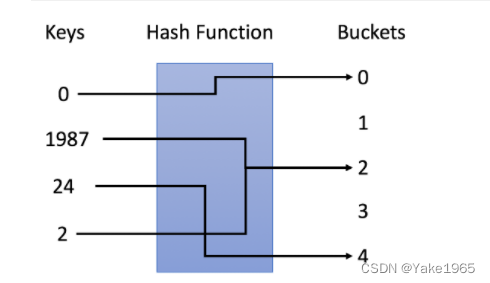
使用 y = x ％ 5 作为哈希函数。

插入：通过哈希函数解析键，将它们映射到相应的桶中。
- 例如，1987 分配给桶 2，而 24 分配给桶 4。
搜索：通过相同的哈希函数解析键，并仅在特定存储桶中搜索。
- 如果搜索 1987，将使用相同的哈希函数将1987 映射到 2。因此在桶 2 中搜索，在那个桶中成功找到了 1987。
- 例如，如果搜索 23，将映射 23 到 3，并在桶 3 中搜索。发现 23 不在桶 3 中，这意味着 23 不在哈希表中。

哈希函数

哈希函数是哈希表中最重要的组件，该哈希表用于将键映射到特定的桶。在上一示例中，使用 y = x % 5 作为散列函数，其中 x 是键值，y 是分配的桶的索引。

散列函数将取决于键值的范围和桶的数量。

哈希函数的设计是一个开放的问题。其思想是尽可能将键分配到桶中，理想情况下，完美的哈希函数将是键和桶之间的一对一映射。然而，在大多数情况下，哈希函数并不完美，它需要在桶的数量和桶的容量之间进行权衡。

冲突解决

理想情况下，如果哈希函数是完美的一对一映射，将不需要处理冲突。不幸的是，在大多数情况下，冲突几乎是不可避免的。例如，在之前的哈希函数（y = x ％ 5）中，1987 和 2 都分配给了桶 2，这是一个冲突。

冲突解决算法应该解决以下几个问题：

如何组织在同一个桶中的值？
如果为同一个桶分配了太多的值，该怎么办？
如何在特定的桶中搜索目标值？

根据我们的哈希函数，这些问题与桶的容量和可能映射到同一个桶的键的数目有关。

假设存储最大键数的桶有 N 个键。

通常，如果 N 是常数且很小，可以简单地使用一个数组将键存储在同一个桶中。如果 N 是可变的或很大，可能需要使用高度平衡的二叉树来代替.。

705. 设计哈希集合

设计哈希集合（HashSet）。HashSet 是指能 O(1) 时间内进行插入和删除，可以保存不重复元素的一种数据结构。
HashSet 是在 时间和空间 上做权衡的经典例子：如果不考虑空间，可以直接设计一个超大的数组，使每个key 都有单独的位置，则不存在冲突；如果不考虑时间，可以直接用一个无序的数组保存输入，每次查找的时候遍历一次数组。

为了时间和空间上的平衡，HashSet 基于数组实现，并通过 hash 方法求键 key 在数组中的位置，当 hash 后的位置存在冲突的时候，再解决冲突。

设计 hash 函数需要考虑两个问题：

通过 hash 方法把键 key 转成数组的索引：设计合适的 hash 函数，一般都是对分桶数取模 % 。
处理碰撞冲突问题：拉链法和线性探测法。

拉链法

定义了一个比较小的数组，然后使用 hash 方法来把求出 key 应该出现在数组中的位置；但是由于不同的 key 在求完 hash 之后，可能会存在碰撞冲突，所以数组并不直接保存元素，而是每个位置都指向了一条链表（或数组）用于存储元素。

在查找一个 key 的时候需要两个步骤：① 求 hash 到数组中的位置；② 在链表中遍历找 key。

优点：可以把数组大小设计比较合理，从而节省空间；不用预知 key 的范围；方便扩容。
缺点：需要多次访问内存，性能上比超大数组的 HashSet 差；需要设计合理的 hash 方法实现均匀散列；如果链表比较长，则退化成 O(N) 的查找；实现比较复杂；

在具体实现中，把拉链设计成了基于「数组」的实现（也可以基于链表）。
「拉链数组」有两种设计方法：①定长拉链数组；②不定长拉链数组。

1、定长拉链数组

这个方法本质上就是把 HashSet 设计成一个 M * NM?N 的二维数组。第一个维度用于计算 hash 分桶，第二个维度寻找 key 存放具体的位置。用了一个优化：第二个维度的数组只有当需要构建时才会产生，这样可以节省内存。

优点：两个维度都可以直接计算出来，查找和删除只用两次访问内存。
缺点：需要预知数据范围，用于设计第二个维度的数组大小。

class MyHashSet:

    def __init__(self):
        self.buckets = 1000
        self.itemsPerBucket = 1001
        self.table = [[] for _ in range(self.buckets)]

    def hash(self, key):
        return key % self.buckets
    
    def pos(self, key):
        return key // self.buckets
    
    def add(self, key):
        hashkey = self.hash(key)
        if not self.table[hashkey]:
            self.table[hashkey] = [0] * self.itemsPerBucket
        self.table[hashkey][self.pos(key)] = 1
        
    def remove(self, key):
        hashkey = self.hash(key)
        if self.table[hashkey]:
            self.table[hashkey][self.pos(key)] = 0

    def contains(self, key):
        hashkey = self.hash(key)
        return (self.table[hashkey] != []) and (self.table[hashkey][self.pos(key)] == 1)

时间复杂度：O(1)
空间复杂度：O(数据范围)

2、不定长拉链数组

不定长的拉链数组是说拉链会根据分桶中的 key 动态增长，更类似于真正的链表。

分桶数一般取质数，这是因为经验上来说，质数个的分桶能让数据更加分散到各个桶中。

优点：节省内存，不用预知数据范围；
缺点：在链表中查找元素需要遍历。

class MyHashSet:

    def __init__(self):
        self.buckets = 1009
        self.table = [[] for _ in range(self.buckets)]

    def hash(self, key):
        return key % self.buckets
    
    def add(self, key):
        hashkey = self.hash(key)
        if key in self.table[hashkey]:
            return
        self.table[hashkey].append(key)
        
    def remove(self, key):
        hashkey = self.hash(key)
        if key not in self.table[hashkey]:
            return
        self.table[hashkey].remove(key)

    def contains(self, key):
        hashkey = self.hash(key)
        return key in self.table[hashkey]

时间复杂度：O(N/b)，N 是元素个数，b 是桶数。
空间复杂度：O(N)

706. 设计哈希映射

HashMap 和 HashSet 的区别是 HashMap 保存的每个元素 key-value 对，而 HashSet 保存的是某个元素 key 是否出现过。
定长拉链数组

class MyHashMap(object):

    def __init__(self):
        self.map = [[-1] * 1000 for _ in range(1001)]

    def put(self, key, value):
        row, col = key // 1000, key % 1000
        self.map[row][col] = value

    def get(self, key):
        row, col = key // 1000, key % 1000
        return self.map[row][col]

    def remove(self, key):
        row, col = key // 1000, key % 1000
        self.map[row][col] = -1

不定长拉链数组

class MyHashMap:

    def __init__(self):
        self.buckets = 1009
        self.table = [[] for _ in range(self.buckets)]

    def hash(self, key):
        return key % self.buckets
    
    def put(self, key: int, value: int) -> None:
        hashkey = self.hash(key)
        for item in self.table[hashkey]:
            if item[0] == key:
                item[1] = value
                return
        self.table[hashkey].append([key, value])

    def get(self, key: int) -> int:
        hashkey = self.hash(key)
        for item in self.table[hashkey]:
            if item[0] == key:
                return item[1]
        return -1

    def remove(self, key: int) -> None:
        hashkey = self.hash(key)
        for i, item in enumerate(self.table[hashkey]):
            if item[0] == key:
                self.table[hashkey].pop(i)
                return

所谓拉链法，指的是，把 key 按照某个数 buckets 的余数，把 key 放进 buckets 个小桶里。在这个小桶里，像拉链一样，藏着很多 key % buckets 相等的 key 值，对应着这个 key 的，就是相应的 value。这就相当于，把 key 按照余数先分了个类，定位这个类的时间复杂度为 O(1)，但接下来去找拉链，就要一个一个地找了。这样，就在时间和存储 key 需要的空间上做出了权衡。其中，buckets 一般取质数，余数的分布会均匀一些。

class MyHashMap:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.buckets = 1009
        self.table = [[] for _ in range(self.buckets)]

    def put(self, key: int, value: int) -> None:
        """
        value will always be non-negative.
        """
        hashkey = key % self.buckets
        for item in self.table[hashkey]:
            if item[0] == key:
                item[1] = value
                return
        self.table[hashkey].append([key, value])


    def get(self, key: int) -> int:
        """
        Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key
        """
        hashkey = key % self.buckets
        for item in self.table[hashkey]:
            if item[0] == key:
                return item[1]
        return -1


    def remove(self, key: int) -> None:
        """
        Removes the mapping of the specified value key if this map contains a mapping for the key
        """
        hashkey = key % self.buckets
        for i, item in enumerate(self.table[hashkey]):
            if item[0] == key:
                self.table[hashkey].pop(i)

时间复杂度： O(n/b) 其中 n 为哈希表中元素的数量，b 为 buckets 的数量。
空间复杂度： O(n)

质数取模，其实是利用了同余的概念：当元素是个有规律的等差数列时，并且和基数（数组大小）最大公约数不为 1 时，就会造成哈希映射时冲突变高（数组某些位置永远不会有值）。比如数列 0,6,12,18,24,30…，base 为 10，取模 (0,6,2,8,4,0…)后，放入哈希表中位置将只能在 0,2,4,6,8 这几个数组位置上；但我们如果把 base 取 7（数组大小甚至比 10 小），同样数列取模后 (0,6,5,4,3,2,1,0,…)，可以分布在哈希表中的 0,1,2,3,4,5,6 所有位置上；若 x 和 y 的最大公约为 z，x 和 y 的最小公倍数就为 (xy)/z，很明显，若 z 为 1，也就是俩数的最大公约数为 1 的时候，那么俩数的最小公倍数就为 xy。

那么当一个数为质数时，除了其自身的倍数外，其余数和其的最大公约数都将是 1，这时，步长选任何数（除了倍数）都可以满足桶的均匀分布。

所以，以取模计算哈希值在桶中的位置是用一个质数当作基数时可以使得哈希表中每个位置都“有用武之地”。

217. 存在重复元素

class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        s = set()
        for x in nums:
            if x in s: return True
            s.add(x)
        return False

136. 只出现一次的数字

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        x = 0
        for y in nums:
            x ^= y
        return x

349. 两个数组的交集

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        if len(nums1) == 0 or len(nums2) == 0:  return []
        nums1.sort()
        nums2.sort()
        ans = set()
        i = j = 0
        while i < len(nums1) and j < len(nums2):
            if nums1[i] < nums2[j]: i += 1
            elif nums1[i] > nums2[j]: j += 1
            else: 
                ans.add(nums1[i])
                i += 1
                j += 1
        return list(ans)
        def binary_search(target, i, j):
            while i < j:
                mid = i + j >> 1
                if nums1[mid] < target: i = mid + 1
                else: j = mid
            if nums1[i] == target:
                assert i == j
                return i
            return -1

        ol, hi = 0, len(nums1) - 1
        for x in nums2:
            idx = binary_search(x, ol, hi)
            if idx == -1: continue
            else:
                ol = idx
                if nums1[idx] not in ans:
                    ans.append(nums1[idx])
        return ans

202. 快乐数

class Solution:
    def isHappy(self, n: int) -> bool:
        # # 方法一：直接尝试
        # for _ in range(6): # 尝试 6 次就够了
        #     n = sum(int(x)**2 for x in str(n))            
        #     if n == 1: return True
        # return False
        # # 方法二：用集合判断循环
        # seen = set() # 一个数再次看到说明进入循环
        # while n != 1 and n not in seen:
        #     seen.add(n)
        #     n = next(n)
        # return n == 1

        # # 计算各位数字的平方和
        def next(n):
            s = 0
            while n > 0:
                n, m = divmod(n, 10)
                s += m ** 2
            return s
        # 方法三：快慢指针
        slow, fast = n, next(n)
        while fast != 1 and slow != fast:
            slow = next(slow)
            fast = next(next(fast))
        return fast == 1