大O表示法和引例
假设检查一个元素需要1毫秒,对于100个元素:
?二分查找:7毫秒(log2(100)大约为7)。
?简单查找:最多需要100毫秒,大约为简单查找的15倍。
现在,假如要帮NASA编写飞船着陆查找算法。需要在10秒内从10亿个元素的列表,简单查找和二分查找需要多长时间呢?


??二分查找:30毫秒(log21000000000大约为30)。
?一种想法是:二分查找的速度大约为简单查找的15倍
则简单查找需要30 ×15 = 450毫秒
符合在10秒内着陆查找完毕的要求。这正确吗?
?答案是错得离谱!因为二分查找和简单查找的运行时间的增速不同。随着列表的增长,二分查找的速度比简单查找快得多。

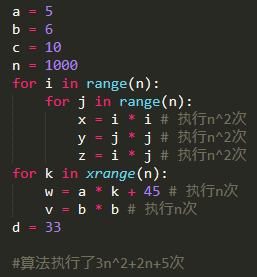
综合起来:如果一个算法的执行次数是 T(n),那么只保留最高次项,同时忽略最高项的系数后得到函数 f(n),此时算法的时间复杂度就是 O(f(n))。
?算法的速度并不能简单以执行时间作为衡量标准。
?随着输入数据的量级不断增大,操作数的增速是不同的。
?这正是大O表示法的用武之地。
?之所以称为大O表示法,是因为操作数前有个大O。
?时间复杂度:
将算法执行运算的操作数丢弃掉低阶项,再去掉所有系数。
在它前面加一个O,就是大O表示法。
?假设使用简单查找在电话簿中找人。
?如果电话簿中第一个人“张三”恰好是我们要查找的对象,这样一次就能找到,无需查看每个条目。考虑到一次就找到了“张三”,请问这种算法的运行时间是O(n)还是O(1)呢?
实际上简单查找的运行时间总是为O(n)。查找张三时,一次就找到了,这是最佳的情形,但大O表示法表示的是最糟的情形。
在最糟情况下,必须查看电话簿中的每个条目,对应的运行时间为O(n)。
 ? ? ? ? ? ? ? ? ? ? ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? ??
O(1)? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?O(n)
O(n2)
?以下从快到慢,列出5种常用大O运行时间
?O(log n),也叫对数时间,如二分查找。
?O(n),也叫线性时间,如简单查找。
?O(n * log n),如之后将介绍的快速排序——一种速度较快的排序算法。
?O(n2),如之后将介绍的选择排序——一种速度较慢的排序算法。
?O(n!),非常慢的算法。

?
?O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
旅行商问题用大O表示法就是O(n!)
np完全问题
?二分查找的速度比简单查找快得多。
?O(logn)比O(n)快,需要搜索的元素越多,前者比后者就快得越多。
?算法运行时间并不以秒为单位。
?算法运行时间是从其增速的角度度量的。
?算法运行时间用大O表示法表示
排序与排序算法
?排序与排序算法
?排序就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
?排序算法(Sorting algorithm)则是一种能将一串数据依照特定的方式进行排列的一种算法。
?排序可以使数据更具结构性,有利于处理。对一些信息处理工作,排序的数据更容易用,排序也是许多算法的重要组成部分。
?排序后的序列可以采用二分法查找(效率高)
?许多算法里需要对计算中使用的数据排序
?Kruskal算法需要对图中的边按权排序
?最佳二叉树生成算法需要数据项按关键码排序
?相比于抽象讨论排序问题,我们更关心计算机的排序方法(排序算法)
?有些算法很直观朴素,描述简单,但通常效率较低
?有些算法更深刻地反映了排序问题的某些本质,因此效率较高,但通常也更复杂一些
?对于小型集合,采用复杂的排序算法可能得不偿失;对于大型集合,需要尽可能充分地利用各种改善措施。
?经典排序算法分类
?比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
?非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。

??相关概念
?稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
?不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面。
?时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
?空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。

冒泡排序:最好的情况是数据本来就有序,复杂度为O(n);最差的情况是O(),稳定算法。
选择排序:最好的情况是数据本来就有序,复杂度为O(n);最差的情况是O(),不稳定算法
直接插入排序:最好的情况是数据本来就有序,复杂度为O(n);最差的情况是O(),稳定算法
希尔排序:最好的情况复杂度为O(n);最差的情况是O(),但平均复杂度要比直接插入小,不稳定算法
快速排序:最好的情况复杂度为NlogN,最差的情况是O(),快速排序将不幸退化为冒泡排序;不稳定(比如序列5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱)
归并排序:所有情况下都是NlogN,稳定算法。
冒泡排序VS选择排序
?冒泡排序当相邻两个元素大小一致时,这一步操作就不需要交换位置,因此冒泡排序是一种严格的稳定排序算法,它不改变序列中相同元素之间的相对位置关系。
?选择排序举例说明:序列58539.我们知道第一遍选择第1个元素“5”会和元素“3”交换,那么原序列中的两个相同元素“5”之间的前后相对顺序就发生了改变。因此,我们说选择排序不是稳定的排序算法,它在计算过程中会破坏稳定性。
?两种算法时间复杂度都是O(n2)
希尔排序
?希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
?希尔排序是基于插入排序的以下两点性质而提出改进方法的:
?插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
?但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
?1959年Shell发明,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
?希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
?如何切分列表是希尔排序的关键——并不是连续切分,而是使用增量i(有时称作步长)选取所有间隔为i的元素组成子列表。
排序代码一览
希尔排序


插入排序
def insert_sort(li):
for i in range(1,len(li)):# i 表示摸到牌的下标
tmp=li[i]
j=i-1#j指的是手里牌的下标
while j>=0 and li[j]>tmp:
li[j+1]=li[j]
j -=1
li[j+1]=tmp
print(li)
li=[3,2,4,1,5,7,9]
print(li)
insert_sort(li)快速排序
from turtle import left
def partition(li,left,right):
tmp=li[left]
while left <right:
while left <right and li[right]>=tmp:#从右边找比tmp小的数
right -=1 #往左走一步
li[left]=li[right] #找到小于的了,替换
print(li,'right')
while left <right and li[left]<=tmp:#从右边找比tmp小的数
left+=1 #往左走一步
li[right]=li[left] #找到小于的了,替换
print(li,'left')
li[left]=tmp
return left
def _quick_sort(li,left,right):
if left<right:#至少两个元素
mid=partition(li,left,right)
_quick_sort(li,left,mid-1)
_quick_sort(li,mid+1,right)
def quick_sort(li):
_quick_sort(li,0,len(li)-1)
li=[5,7,6,3,4,1,2,9,8]
print(li)
_quick_sort(li,0,len(li)-1)
print(li)
##时间复杂度是o(nlog n)冒泡排序
import random
def bubble_sort(li):
for i in range(len(li)-1):
for j in range(len(li)-i-1):
if li[j]>li[j+1]:
li[j],li[j+1]=li[j+1],li[j]
exchange=True
print(i)
print(li)
if not exchange:
return
li=[8,6,48,4,3,87,7,34,1]
print(li)
bubble_sort(li)
选择排序
def selectionSort(alist):
for fillslot in range(len(alist)-1, 0, -1):
positionOfMax = 0
for location in range(1, fillslot):
if alist[location] > alist[positionOfMax]:
positionOfMax = location
temp = alist[fillslot] ##最大那个
alist[fillslot] = alist[positionOfMax]
alist[positionOfMax] = temp
print(alist)
##时间复杂度为n方,有着两个for循环
#比冒泡更快
#长5 fillslot 4 0 -1 location 1 ,5
# 3 0 -1 1 4
li=[8,6,48,4,3,87,7,34,1]
print(li)
selectionSort(li)