一、栈和队列
栈和队列都是对结点操作位置有要求的特殊线性表
栈(先进后出)----->子弹入膛
队列(先进先出)----->食堂排队
二、栈(数据结构)
1.概念
?? ?线性表的插入(压栈)和删除(出栈)都只能在同一个端点进行,不能在其他位置,这样的结构称之为栈
2.分类
?? ?顺序栈、链式栈(带头结点的单向不循环链表)
3.特性
?? ?后进先出,一端是完全封死的,只有另外一端是用来控制和插入的,所以说,最先进来的结点肯定是最后出去的
4.链式栈(stack)
?? ?其实就是一个头插头删或者尾插尾删的链表
三、链式栈的设计和创建
1.设计:
typedef int SElemType_t;
//数据结点
struct node
{
?? ?SElemType_t data;
?? ?struct node *next;
};
//链式栈的管理结构体(头结点)
struct list_stack
{
?? ??? ?struct node *stack;//保存首结点的地址
?? ??? ?int size;//栈结构体中元素的个数(结点个数)
};
struct list_stack *managerStack;
//2.初始化栈
bool init_stack()
{
?? ?//1)申请栈管理结构体的内存空间
?? ?managerStack=malloc(sizeof(struct list_stack));
?? ?if(managerStack==NULL)
?? ?{
?? ??? ?printf("malloc managerStack error\n");
?? ??? ?return false;
?? ?}
?? ?//2)初始化
?? ?managerStack->size=0;
?? ?managerStack->stack=NULL;
?? ?return true;
}
//3.入栈(压栈)
bool push(SElemType_t inputData)
{
?? ?//1、申请栈元素的结点的内存空间
?? ?struct node *newNode=malloc(sizeof(struct node));
?? ?if(newNode==NULL)
?? ?{
?? ??? ?printf("malloc newNode error\n");
?? ??? ?return false;
?? ?}
?? ?//2、初始化
?? ?newNode->data=inputData;
?? ?newNode->next=NULL;
?? ?//3、插入
?? ?if(managerStack->stack==NULL)//从无到有
?? ?{
?? ??? ?managerStack->stack=newNode;
?? ?}
?? ?else//(由少到多)(头插)
?? ?{
?? ??? ?newNode->next=managerStack->stack;
?? ??? ?//更新首结点
?? ??? ?managerStack->stack=newNode;
?? ?}
?? ?//栈元素+1
?? ?managerStack->size++;
?? ?return true;
}
bool isEmpty()
{
?? ?return managerStack->size==0;
}
//出栈--删除(头删)
bool pop(SElemType_t *outData)
{
?? ?//1、先判断当前有没有栈元素
?? ?if(isEmpty())
?? ??? ?return false;
?? ?//2、先获取出栈的数据
?? ?*outData=managerStack->stack->data;
?? ?//先定义一个临时的指针存储当前删除结点的地址
?? ?struct node*delNode=managerStack->stack;
?? ?//更新首结点
?? ?managerStack->stack=delNode->next;
?? ?//释放
?? ?free(delNode);
?? ?//size--
?? ?managerStack->size--;
?? ?return true;
}
//销毁栈
void destory_stack()
{
?? ?if(managerStack==NULL)
?? ??? ?return;
?? ?//1.遍历所有的结点,每个点都删除
?? ?struct node *p=managerStack->stack;
?? ?struct node *pnext=NULL;
?? ?while(p)
?? ?{
?? ??? ?pnext=p->next;
?? ??? ?free(p);
?? ??? ?p=pnext;
?? ?}
?? ?//2.释放头结点(栈管理结构体)
?? ?free(managerStack);
?? ?managerStack=NULL;
}demo.c
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int SElemType_t;
struct node{
SElemType_t data;
struct node *next;
};
struct list_stack
{
struct node *stack;
int size;
};
struct list_stack *managerStack;
bool init_stack()
{
managerStack = malloc(sizeof(struct list_stack));
if(managerStack == NULL)
{
printf("malloc managerStack error\n");
return false;
}
managerStack->size = 0;
managerStack->stack = NULL;
return true;
}
bool push(SElemType_t inputData)
{
struct node *newNode = malloc(sizeof(struct node));
if(newNode==NULL)
{
printf("malloc newNode error\n");
return false;
}
newNode->data = inputData;
newNode->next = NULL;
if(managerStack->stack == NULL)
{
managerStack->stack = newNode;
}
else
{
newNode->next = managerStack->stack;
managerStack->stack = newNode;
}
managerStack->size++;
return true;
}
bool isEmpty()
{
return managerStack->size==0;
}
//出栈--删除(头删)
bool pop(SElemType_t *outData)
{
//1、先判断当前有没有栈元素
if(isEmpty())
return false;
//2、先获取出栈的数据
*outData=managerStack->stack->data;
//先定义一个临时的指针存储当前删除结点的地址
struct node*delNode=managerStack->stack;
//更新首结点
managerStack->stack=delNode->next;
//释放
free(delNode);
//size--
managerStack->size--;
return true;
}
//销毁栈
void destory_stack()
{
if(managerStack==NULL)
return;
//1.遍历所有的结点,每个点都删除
struct node *p=managerStack->stack;
struct node *pnext=NULL;
while(p)
{
pnext=p->next;
free(p);
p=pnext;
}
//2.释放头结点(栈管理结构体)
free(managerStack);
managerStack=NULL;
}
void main()
{
int data;
init_stack();
push(10);
push(20);
push(30);
push(40);
while(pop(&data))
{
printf("%d\n",data);
}
destory_stack();
}
//练习:使用链式栈实现10进制转8进制
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int SElemType_t;
struct node{
SElemType_t data;
struct node *next;
};
struct list_stack
{
struct node *stack;
int size;
};
struct list_stack *managerStack;
bool init_stack()
{
managerStack = malloc(sizeof(struct list_stack));
if(managerStack == NULL)
{
printf("malloc managerStack error\n");
return false;
}
managerStack->size = 0;
managerStack->stack = NULL;
return true;
}
bool isEmpty()
{
return managerStack->size==0;
}
//出栈--删除(头删)
bool pop(SElemType_t *outData)
{
//1、先判断当前有没有栈元素
if(isEmpty())
return false;
//2、先获取出栈的数据
*outData=managerStack->stack->data;
//先定义一个临时的指针存储当前删除结点的地址
struct node*delNode=managerStack->stack;
//更新首结点
managerStack->stack=delNode->next;
//释放
free(delNode);
//size--
managerStack->size--;
return true;
}
//销毁栈
void destory_stack()
{
if(managerStack==NULL)
return;
//1.遍历所有的结点,每个点都删除
struct node *p=managerStack->stack;
struct node *pnext=NULL;
while(p)
{
pnext=p->next;
free(p);
p=pnext;
}
//2.释放头结点(栈管理结构体)
free(managerStack);
managerStack=NULL;
}
bool push(SElemType_t inputData)
{
struct node *newNode = malloc(sizeof(struct node));
if(newNode==NULL)
{
printf("malloc newNode error\n");
return false;
}
newNode->data = inputData;
newNode->next = NULL;
if(managerStack->stack == NULL)
{
managerStack->stack = newNode;
}
else
{
newNode->next = managerStack->stack;
managerStack->stack = newNode;
}
managerStack->size++;
return true;
}
void turn(SElemType_t data)
{
if(data == 0)
return;
else
{
push(data%8);
turn(data/8);
return;
}
}
int main(int argc,char *argv[])
{
int data;
init_stack();
printf("pls input data:\n");
scanf("%d",&data);
turn(data);
while(pop(&data))
{
printf("%d",data);
}
printf("\n");
destory_stack();
return 0;
}一、队列
1、概念
?? ?线性表的插入(入队)在指定的一端,删除(出队)必须在另外一端,不能在其他位置,这种线性表称之为队列。
?? ?特性:先进先出
2、分类
?? ?链式队列 顺序队列
3、设计数据结点和队列管理结构体
typedef int QElemType_t;
struct list_queue *managerQueue;//保存链式队列的管理结构体
//数据结点
struct node
{
?? ?QElemType_t data;
?? ?struct node *next;
};
//链式队列的管理结构体(头结点)
struct list_queue
{
?? ?struct node *first;//队头--相当于之前数据的首结点
?? ?struct node *last;//队尾--数据的尾结点
?? ?int size;//元素的个数
};
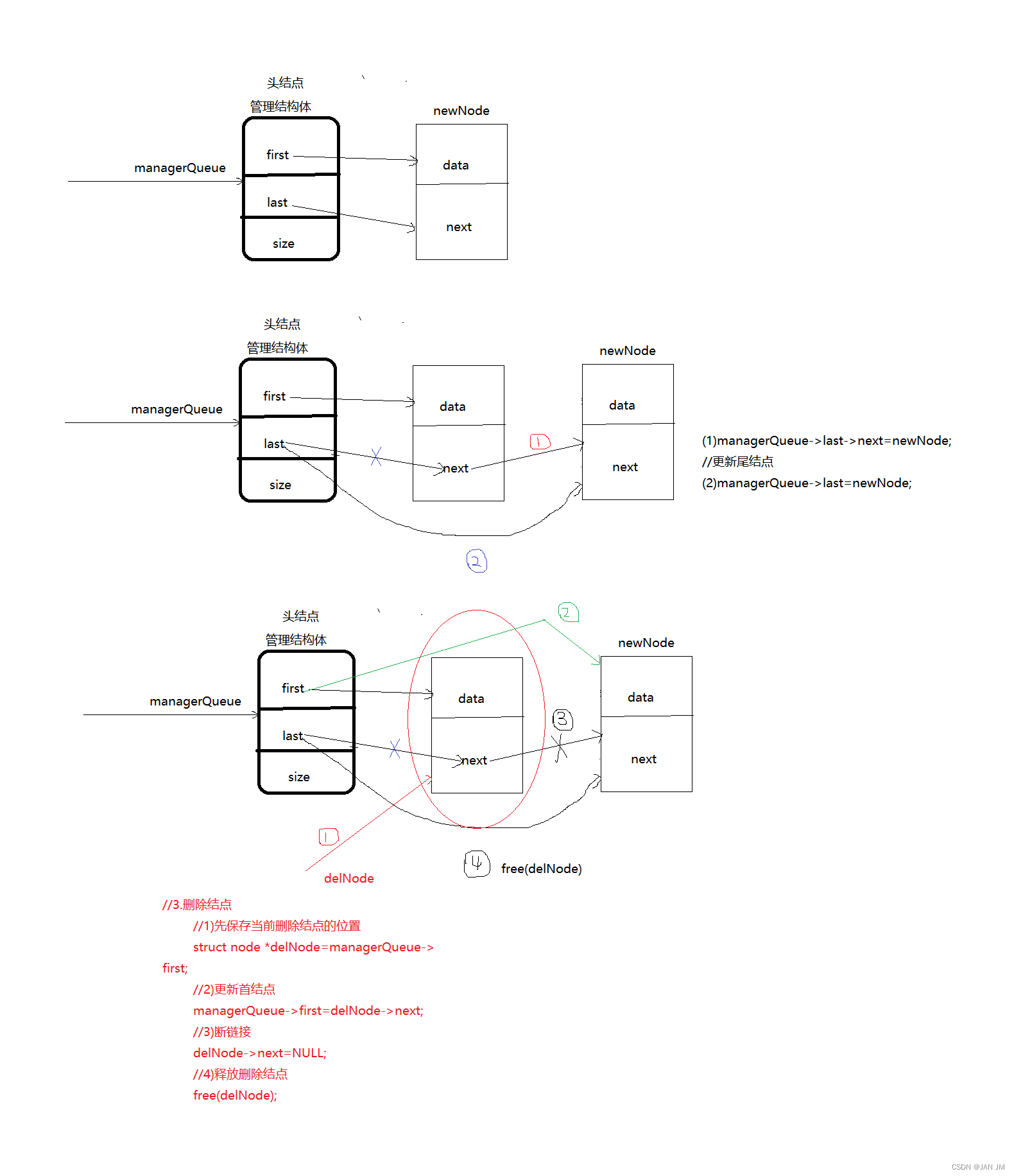
//实现尾插头删(先进先出)
//入队--尾插(新建一个结点,插入到链表中)
bool enter_queue(QElemType_t inputdata)
{
?? ?//1.新建结点,并且初始化
?? ?struct node *newNode=malloc(sizeof(struct node));
?? ?if(newNode==NULL)
?? ?{
?? ??? ?printf("malloc newNode error\n");
?? ??? ?return false;
?? ?}
?? ?newNode->data=inputdata;
?? ?newNode->next=NULL;
?? ?//2.尾插
?? ?//1)从无到有----刚开始没有数据结点,插入的第一个结点是数据的首结点也是尾结点
?? ?if(managerQueue->first==NULL)
?? ?{
?? ??? ?managerQueue->first=managerQueue->last=newNode;
?? ?}
?? ?//2)由少到多
?? ?else
?? ?{
?? ??? ?managerQueue->last->next=newNode;
?? ??? ?//更新尾结点
?? ??? ?managerQueue->last=newNode;
?? ?}
?? ?//3、链式队列的结点个数+1
?? ?managerQueue->size++;
?? ?return true;
}
//判断队列是否为空
bool isEmpty()
{
?? ?return managerQueue->size==0;
}
bool leave_queue(QElemType_t *outdata)
{
?? ?//1.判断是否为空
?? ?if(isEmpty())
?? ?{
?? ??? ?printf("isEmpty\n");
?? ??? ?return false;
?? ?}
?? ?//2、获取数据(从数据的首结点获取数据)
?? ?*outdata=managerQueue->first->data;
?? ?//3.删除结点
?? ?//1)先保存当前删除结点的位置
?? ?struct node *delNode=managerQueue->first;
?? ?//2)更新首结点
?? ?managerQueue->first=delNode->next;
?? ?//3)断链接
?? ?delNode->next=NULL;
?? ?//4)释放删除结点
?? ?free(delNode);
?? ?//5)如果当前队列只有一个结点,此时删除之后,first last都要NULL
?? ?if(managerQueue->first==NULL)
?? ??? ?managerQueue->last=NULL;
?? ?//4.链式队列的结点个数-1
?? ?managerQueue->size--;
?? ?return true;
?? ?
}
//销毁队列
void destory_queue()
{
?? ?if(managerQueue==NULL)
?? ?return;
?? ?//遍历队列的所有结点
?? ?struct node *p=managerQueue->first;
?? ?struct node *pNext=NULL;
?? ?while(p)
?? ?{
?? ??? ?pNext=p->next;
?? ??? ?free(p);
?? ??? ?p=pNext;
?? ?}
?? ?//释放队列管理结构体
?? ?free(managerQueue);
?? ?managerQueue->NULL;
?? ?
}
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int QElemType_t;
struct list_queue *managerQueue;//保存链式队列的管理结构体
//数据结点
struct node
{
QElemType_t data;
struct node *next;
};
//链式队列的管理结构体(头结点)
struct list_queue
{
struct node *first;//队头--相当于之前数据的首结点
struct node *last;//队尾--数据的尾结点
int size;//元素的个数
};
//创建一条链式队列
bool init_queue()
{
//1)申请队列的管理结构体内存空间
managerQueue=malloc(sizeof(struct list_queue));
if(managerQueue==NULL)
{
printf("managerQueue malloc error\n");
return false;
}
//2)初始化
managerQueue->first=NULL;
managerQueue->last=NULL;
managerQueue->size=0;
return true;
}
//实现尾插头删(先进先出)
//入队--尾插(新建一个结点,插入到链表中)
bool enter_queue(QElemType_t inputdata)
{
//1.新建结点,并且初始化
struct node *newNode=malloc(sizeof(struct node));
if(newNode==NULL)
{
printf("malloc newNode error\n");
return false;
}
newNode->data=inputdata;
newNode->next=NULL;
//2.尾插
//1)从无到有----刚开始没有数据结点,插入的第一个结点是数据的首结点也是尾结点
if(managerQueue->first==NULL)
{
managerQueue->first=managerQueue->last=newNode;
}
//2)由少到多
else
{
managerQueue->last->next=newNode;
//更新尾结点
managerQueue->last=newNode;
}
//3、链式队列的结点个数+1
managerQueue->size++;
return true;
}
//判断队列是否为空
bool isEmpty()
{
return managerQueue->size==0;
}
bool leave_queue(QElemType_t *outdata)
{
//1.判断是否为空
if(isEmpty())
{
printf("isEmpty\n");
return false;
}
//2、获取数据(从数据的首结点获取数据)
*outdata=managerQueue->first->data;
//3.删除结点
//1)先保存当前删除结点的位置
struct node *delNode=managerQueue->first;
//2)更新首结点
managerQueue->first=delNode->next;
//3)断链接
delNode->next=NULL;
//4)释放删除结点
free(delNode);
//5)如果当前队列只有一个结点,此时删除之后,first last都要NULL
if(managerQueue->first==NULL)
managerQueue->last=NULL;
//4.链式队列的结点个数-1
managerQueue->size--;
return true;
}
//销毁队列
void destory_queue()
{
if(managerQueue==NULL)
return;
//遍历队列的所有结点
struct node *p=managerQueue->first;
struct node *pNext=NULL;
while(p)
{
pNext=p->next;
free(p);
p=pNext;
}
//释放队列管理结构体
free(managerQueue);
managerQueue=NULL;
}
void main()
{
int outdata;
init_queue();
//入队
enter_queue(10);
enter_queue(20);
enter_queue(30);
enter_queue(40);
enter_queue(50);
//出队
while(leave_queue(&outdata))
{
printf("%d\t",outdata);
}
printf("\n");
destory_queue();
}?
二、顺序队列的实现
顺序队列:队列中每个元素的内存空间都是连续的
typedef int QElemType_t;
struct sequent_queue *managerQueue;//保存顺序队列的管理结构体
//数据结点
struct node
{
?? ?QElemType_t data;
?? ?struct node *next;
};
//顺序队列的管理结构体(头结点)
struct sequent_queue
{
?? ?QElemType_t *queue;//保存连续内存地址的首地址
?? ?int first;//队头
?? ?int last;//队尾
?? ?int size;//队列元素的总个数
};
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int QElemType_t;
struct sequent_queue *managerQueue;//保存顺序队列的管理结构体
//数据结点
struct node
{
QElemType_t data;
struct node *next;
};
//顺序队列的管理结构体(头结点)
struct sequent_queue
{
QElemType_t *queue;//保存连续内存地址的首地址
int first;//队头
int last;//队尾
int size;//队列元素的总个数
};
//创建一个顺序队列并初始化
bool init_queue(int size)
{
//1.申请队列的管理结构体的内存空间
managerQueue=malloc(sizeof(struct sequent_queue));
if(managerQueue==NULL)
{
printf("malloc managerQueue error\n");
return false;
}
//2.初始化
managerQueue->queue=NULL;
managerQueue->first=managerQueue->last=0;
managerQueue->size=size;
//3.申请一片连续的内存空间存储队列元素,其首地址给queue存储
managerQueue->queue=malloc(sizeof(QElemType_t)*size);
if(managerQueue->queue==NULL)
{
free(managerQueue);
managerQueue=NULL;
printf("malloc managerQueue->queue error\n");
return false;
}
return true;
}
bool isFull()
{
return (managerQueue->last+1)%(managerQueue->size)==managerQueue->first;
}
//入队---尾插
bool enter_queue(QElemType_t inputdata)
{
//1.先判断当前顺序队列是否是满的
if(isFull())
{
printf("isFuLL\n");
return false;
}
//2.将数据插入到队列中
managerQueue->queue[managerQueue->last]=inputdata;
//3.队尾往后面偏
managerQueue->last=(managerQueue->last+1)%managerQueue->size;
return true;
}
bool isEmpty()
{
return managerQueue->last==managerQueue->first;
}
//出队
bool leave_queue(QElemType_t *outdata)
{
//1.判断是否为空
if(isEmpty())
{
printf("isEmpty\n");
return false;
}
//2.获取数据first
*outdata=managerQueue->queue[managerQueue->first];
//3.first队头,往后进行偏移
managerQueue->first=(managerQueue->first+1)%managerQueue->size;
return true;
}
//销毁队列
void destory_queue()
{
//1.先释放连续的内存空间
if(managerQueue->queue)
free(managerQueue->queue);
//2.释放队列管理结构体
if(managerQueue)
free(managerQueue);
managerQueue=NULL;
}
void main()
{
init_queue(7);
enter_queue(10);
enter_queue(20);
enter_queue(30);
enter_queue(40);
enter_queue(50);
enter_queue(60);
enter_queue(70);
QElemType_t outdata;
while(leave_queue(&outdata))
{
printf("%d\n",outdata);
}
printf("\n");
destory_queue();
return ;
}
?

?
?三、排序
?排序是处理数据的一种常见的操作,所谓的排序是将数据按某个字段规律排列,
?所说的字段就是数据结点的其中一个属性
?稳定性:在一组无序的数据中,若两个待排序的数据,在排序前后的相对位置没有发生改变,称之为稳定排序
?时间复杂度
?空间复杂度
?不同的排序算法性能不同(选择排序、插入排序、希尔排序、冒泡排序)
?四、算法的复杂度
?1、概念
? 算法指的是用来操作数据、解决问题的一组方法。比如对于同一个问题,
? 使用不同的算法都能够去实现,得到的结果也一样,但是在这个过程中消耗的资源以及时间会有很大区别。
? 主要从算法在运行过程中的“时间”和“空间”两个维度去衡量
?2、分类
?时间复杂度:是指当前算法或者某一段程序所消耗的时间
?空间复杂度:是指执行算法需要占用的内存空间
?3、时间复杂度
?1)如何计算时间复杂度
?取决于这个算法或这段程序的执行次数,并且采用估算值。执行的次数越少,说明使用的时间越少
?2)案例
?int func1()
?{
?? ?printf("11111\n");
?? ?printf("11111\n");
?? ?return 0;
?}
??
? int func2(int n)
?{
?? ?for(int i=0;i<n;i++)
?? ?printf("11111\n");
?? ?
?}
?
?一个算法花费的时间与算法中语句的执行次数成正比,执行次数越多,花费的时间就越多。
?一个算法中的执行次数称为语句频度或时间频度。记为T(n);
?在各种算法中,若算法中的语句执行次数为一个常数,则时间复杂度为o(1)
?
?假设每行代码的执行时间是一样的,那么我们调用一次fun1()函数
?执行次数:3次 所以T(n)=3=O(1);
?n表示输入的参数,当n无穷大时,时间复杂度还是3次,所以规定时间复杂度为常数时,
?时间复杂度的估算值为O(1)
?调用一次func2函数,执行次数:3n+2次 ,所以T(n)=3n+2=O(n);
?
?例子:T(n)=5*n^4+44*n^2+n+55=O(n^4)
?
?总结:取决于T(n)是不是常数
? ? ? ?如果是:时间复杂度O(1)
?? ? ? 如果不是:时间复杂度为O(T(n)的最高次幂)
?? ? ??
?
int fun3(int n)
{
?? ?for(int i=0;i<n;i++)
?? ?{
?? ??? ?for(int j=0;j<n;j++)
?? ??? ??? ?printf("11111\n");
?? ?}
}?
int fun4(int n)
{
?? ?for(int i=0;i<n;i++)
?? ?{
?? ??? ?for(int j=0;j<n;j++)
?? ??? ??? ?printf("11111\n");
?? ?}
?? ?for(int i=0;i<n;i++)
?? ?printf("11111\n");
}
int fun5(int n)
{
?? ?if(n>200)
?? ?{
?? ??? ?for(int i=0;i<n;i++)
?? ??? ?{
?? ??? ??? ?for(int j=0;j<n;j++)
?? ??? ??? ?printf("11111\n");
?? ??? ?}
?? ?
?? ?}
?? ?else
?? ?{
?? ??? ?for(int i=0;i<n;i++)
?? ? ? ?printf("11111\n");
?? ?}
?? ?
}?
调用func3函数一次:里面循环n次,外面的循环也是n,T(n)=O(n^2)
调用func4函数一次:T(n)=O(n^2)
调用func5函数一次: T(n)=O(n^2)
int fun6(int n)
{
?? ?for(int i=0;i<n;i++)
?? ?{
?? ? ? ?for(int j=i;j<n;j++)
?? ??? ?printf("11111\n");
?? ?}
}
当i=0,里面循环n
当i=1,里面n-1
? i=2 ? ?n-2
? i=n-1 ? 1
相加(等差数列的求和公式)
1+2+3+......+(n-1)+n-------->(n*(n+1))/2 =(n^2+n)/2
所以T(n)=O(n^2)
int fun7(int n)
{
?? ?for(int i=1;i<n;i*=2)
?? ?{
?? ??? ?printf("11111\n");
?? ?}
}
当n=8时,printf函数执行次数为3 ? T(8)=3
当n=16时,printf函数执行次数为4 ?T(16)=4
T(8)=3--------->2^3=8
T(16)=4-------->2^4=16 ? ?2^T(n)=n ??
T(n)=log以2为底n的对数 ??
4、空间复杂度
空间复杂度是对算法过程中临时占用内存空间的度量。
空间复杂度:S(n)=O()
void func1(int n)
{
? ? n++;
?? ?int a=2;
?? ?int b=3;
}
调用一次fun1函数,空间复杂度为S(n)=O(1)
void func2(int n)
{
? ? char*p=malloc(n);
?? ?for(int i=0;i<n;i++)
?? ?{
?? ??? ?p[i]=i;
?? ?}
} ??
调用一次fun2函数,空间复杂度为S(n)=O(n);
void fun3(int n)
{
?? ?char ch[n][n];
}
调用一次fun3函数,空间复杂度为S(n)=O(n^2);
5、选择排序
?? ?首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕
#include<stdio.h>
void swap(int *a,int *b) //交換兩個變數
{
int temp = *a;
*a = *b;
*b = temp;
}
//选择排序
void selection_sort(int arr[], int len)
{
int i,j;
for (i = 0 ; i < len - 1 ; i++)
{
int min = i;
for (j = i + 1; j < len; j++) //走訪未排序的元素
if (arr[j] < arr[min]) //找到目前最小值
min = j; //紀錄最小值
swap(&arr[min], &arr[i]); //做交換
}
}
//插入排序
void insertion_sort(int arr[], int len)
{
int i,j,key;
for (i=1;i<len;i++){
key = arr[i];
j=i-1;
while((j>=0) && (arr[j]>key))
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}
void show(int *arr,int len)
{
int i;
for(i=0;i<len;i++)
{
printf("%d\t",arr[i]);
}
printf("\n");
}
int main()
{
int arr[]={15,23,5,6,18};
int len=sizeof(arr)/sizeof(arr[0]);
//selection_sort(arr,len);
insertion_sort(arr,len);
show(arr,len);
return 0;
}
6、插入排序
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。
(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
?
?
?