BV13g41157hK
认识复杂度和简单的排序算法
- 数组:取arr[i]:计算了一个偏移量是一个常数操作,算距离堆偏移量直接把地址拿出来,跟数据量无关
- 实际结构在地址中串着比较乱,跟数据量有关,list.get(i)不是一个常数操作
- 加减乘除是一个常数操作、位运算都是常数操作
- 选择排序:选一个最小值 放在1位置 再在1到最后选择最小放到1位置上 最后不断空间被挤压就成功达到了要求
计算了一下多少次常数操作,只需要取最高次项就为时间复杂度
当同时为O(n)的时候,用理论值无法估计,需要通过实际运行来判断常数项时间。
- 冒泡排序:12比较,23比较,34比较谁大谁往后移动一直放到最后,最后一个一定最大,一定是一个等差数列
- 空间复杂度:额外有限几个变量空间复杂度就是O(1),要开辟数组就是O(n)
- 异或运算:相同为0 不同为1。还可以理解为无进位相加 性质:0异或n=n n异或n=0 满足交换律和结合律和谁先谁后的顺序无关 超级牛逼的异或更改排序方法:a=a^b b=a^b a=a^b 运行一遍之后就可以实现a和b的交换(作用是可以不额外申请一个变量空间)


需要保证a和b的两块内存分属于不同的两部分 否则会被洗成0
题目:全偶数次的数组中有一两种数字为奇数次,找出其中奇数次的数

- 对于第一种情况直接全部异或数组中的每一个数字即可,原理是偶数次异或为0,奇数次异或为这个数
- 对于第二种情况需要全部异或一遍得到a^b
再提取出最右侧的1的写法:int rightone = a &(~a+1) 自己与上他自己的取反加一可以得到一个最右侧1其他全为0的数
只找到其中一位a和b不同再在数组中全部异或这一位为1或者这一位为0的数便可以找到a或者找到b
然后再用这个数字去异或a^b就得到了另外一个数
至于取哪一位就用上面提取最后测1的方法
插入排序
和数据量有关不像我们之前的冒泡排序和选择排序,无论数据量大小多少都要进行相同的操作数
先保证前0-1个有序 再保证0-2个有序 再保证.0-n个有序具体的保证方法是拿这个新的数和前面的数一一对比,找到最合适的位置插入进去
二分思想
在一个已经有序的数组中查找有没有一个数
拿这个数一次又一次的和我们数组的中值作对比并且更改长度
在一个有序数组中找到大于等于一个数的最左的位子
二分找中值 如果已经满足大于这个数取左区间继续二分
局部最小值问题
数组无序,任何两个临近的数不相等,局部最小就是同时小于左边一个元素,同时也小于右边一个元素,在这个数组中只找一个局部最小就可以stop。
左边下滑右边上升,中间一定存在某个低谷
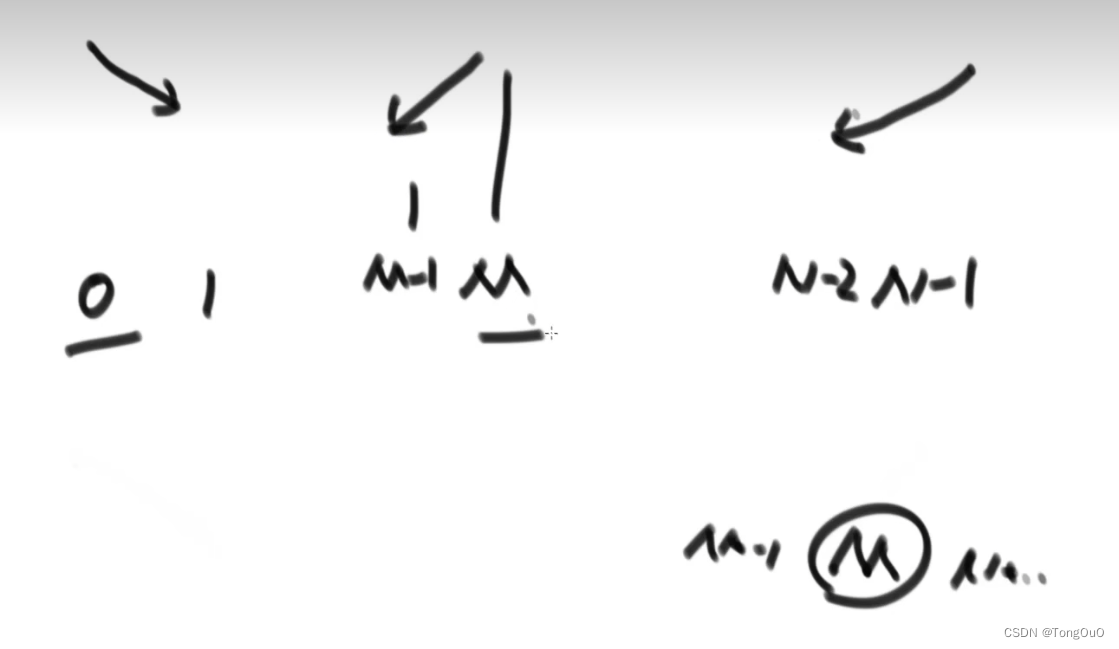
优化策略:1.数据状况特殊:是否有序呀~ 2.问题的标准特殊
具有排他性可以二分 比如左边可能有 右边一定没有
对数器
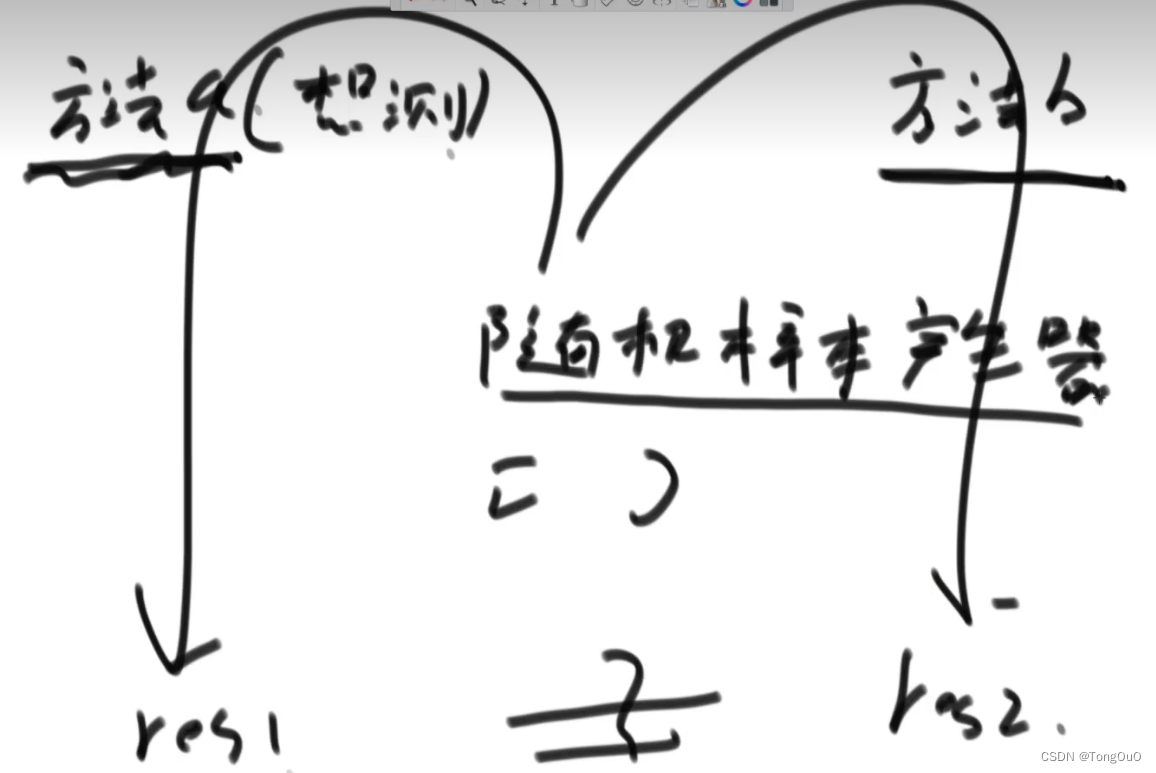
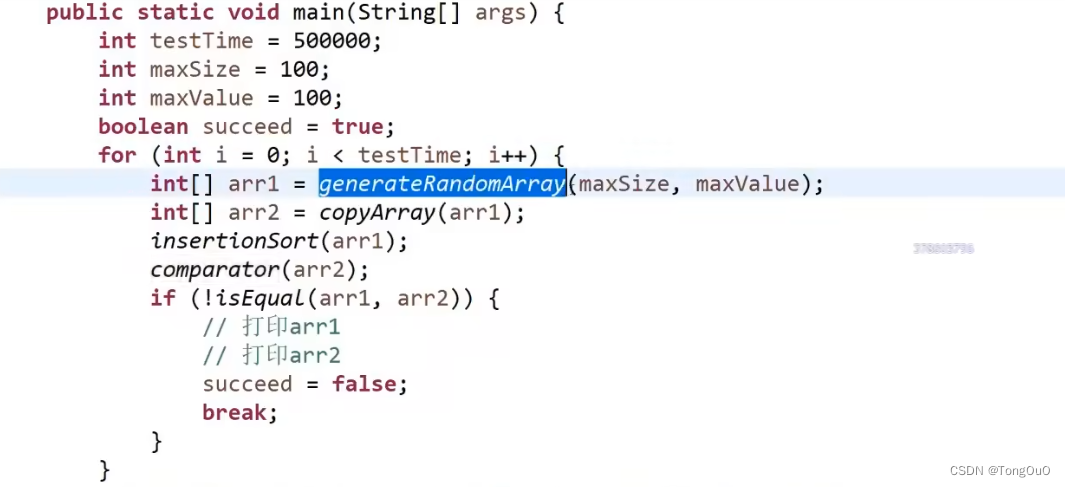
长度随机+值随机
认识O(nlogn)的排序
递归
- 计算中点的时候不用l+r除以2的原因是l+r有可能会溢出不行
使用mid=l+(r-l)/2使用l加一半 或者把除二改为右移一位 - 在一个数组中用递归方法求最大
L=R时候return数组中这个数,否则划分左右两个子区间,分别再次进行这个函数
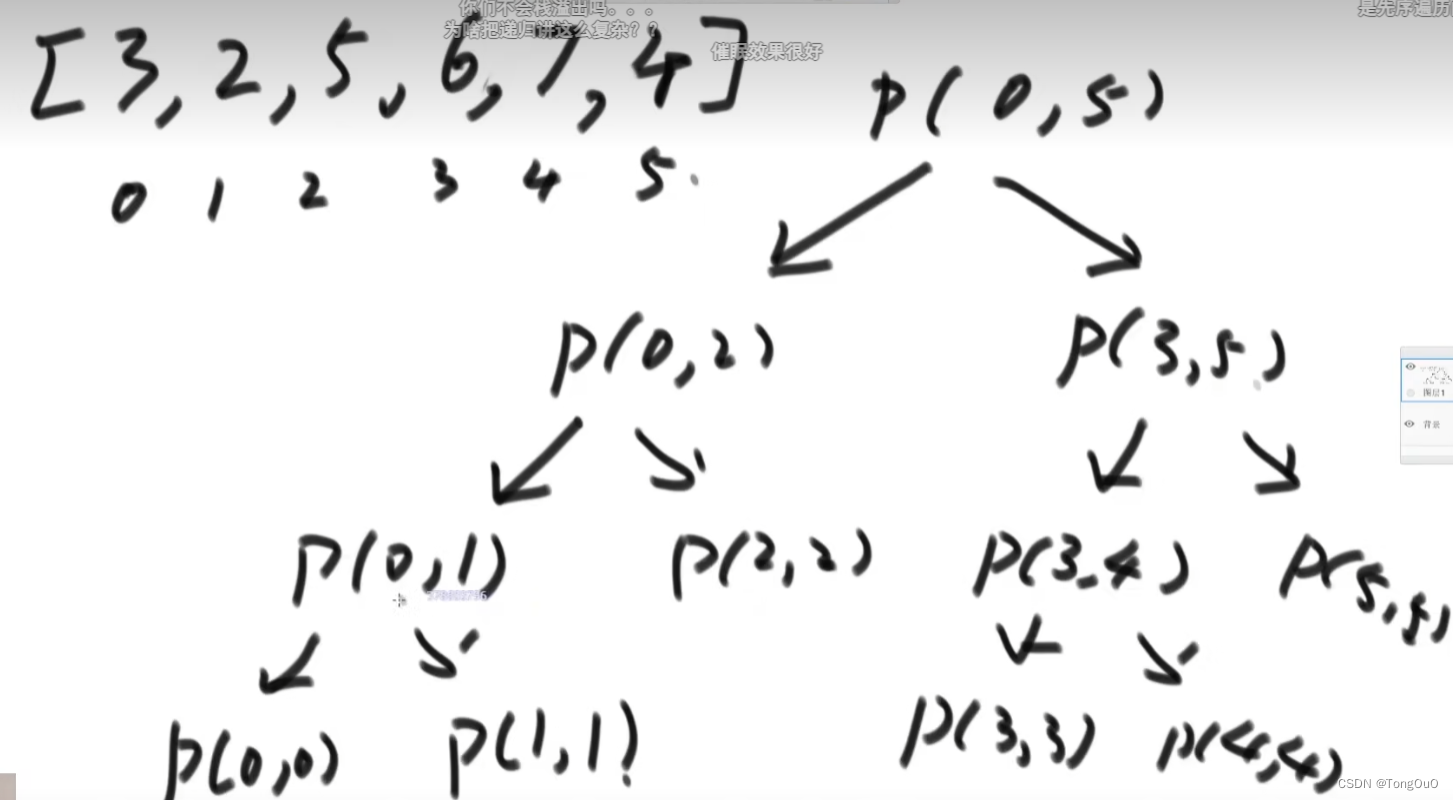
是一个利用栈计算所有树的节点的过程
Master公式

其中T(N/b)为调用子问题时候规模是否等量,a表示子问题在等量的同时被调用了多少次,O(n^d)为除了子过程外剩下过程的时间复杂度,子问题等规模的递归就可以用master公式直接求时间复杂度
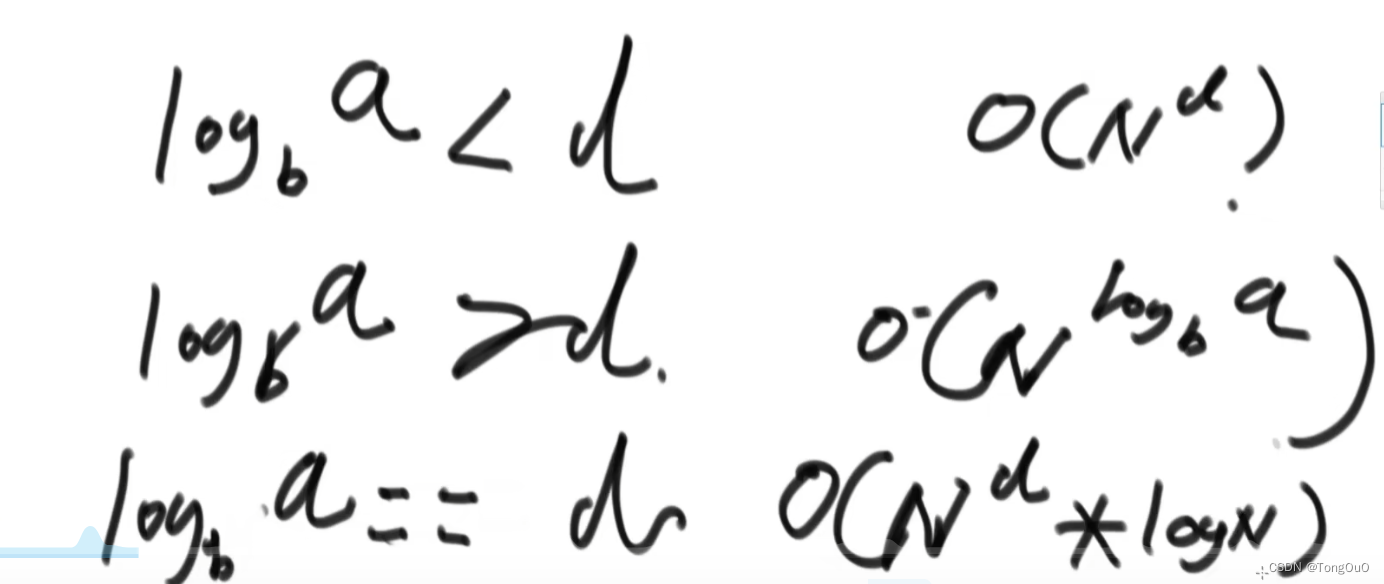
归并排序 MergeSort
为什么时间复杂度会变成nlogn,我们的比较没有被浪费,变成了一个有效的部分归并到更大的部分中去,相比于插入,冒泡排序的效率更高

小和问题(归并扩展)

- 暴力破解法:每个位置i都进行往前的计算暴力法可以得到O(n方)
- O(nlogn)方法:深度改写mergesort,和mergesort的唯一区别的每次排序的时候计算小和,并且在左右相等时候先把右边放入数组
- 逆序对问题(和刚才的小和基本上一样),变成了求左边有多少个比此数大
快速排序(荷兰国旗问题)

不要求排序,只用把小于num的放左边,大于num的放右边
解法:

实质上是动态的修改小于等于区,让小于等于区推着大于区往后走
荷兰国旗问题
让小于的在左边 中间的在中间 右边的在右边
解法:

i和大于区域撞上的时候停止
快速排序
快速排1.0:利用了小于等于放左边大于等于放右边,一次搞定一个数
快速排序2.0:利用了小于放左边,等于放中间,大于放右边,一次可以搞定等于的一批数,荷兰国旗问题
每次取最后一个数来划分
不管是快排1.0还是快排2.0时间复杂度都是O(n方),因为可以举出最差的例子,已经有序的数组每次partation都是一样的,划分值打的很偏产生最差情况
快排3.0版本:为了解决选排序点选偏的问题,我们随机选一个值作为比较值,因为是纯随机,所以数学期望之下也是nlogn的算法
计数排序
统计员工年龄数据,把相同年龄的存到一张表上,只需要根据表上的先后顺序就可以确定根据年龄数据进行排序,时间复杂度On
基数排序
桶排序
数据结构可以是任何东西可以是链表可以是数组或者任何东西
把数字都补成三位,根据个位数字放到对应的桶里面去,根据从小到右边倒出来,再根据十位全部倒一遍,再根据百位倒一遍,最后所有数组倒出来就全部排好序了,这里我们用队列好一点,高位数字优先级最高,从个位开始排,依次进桶,和计数排序的区别是只要是十进制就划出来是个队列就行了,也是基于数据特殊性的非比较算法
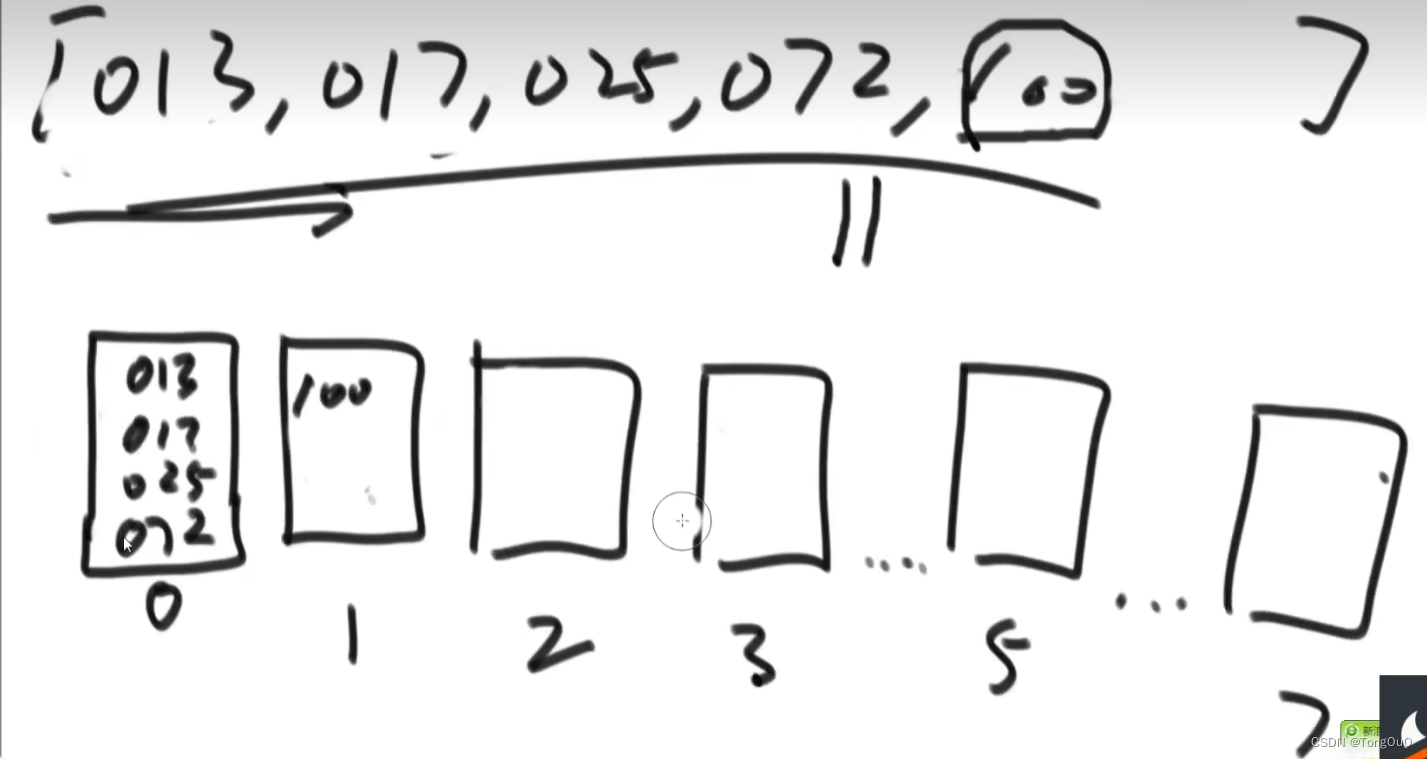
代码具体实现细节:利用了前缀和确定目标数据在辅助数组中的位置完成入桶和出桶的操作,根据入桶所以出桶的时候应该从右到左进行出桶
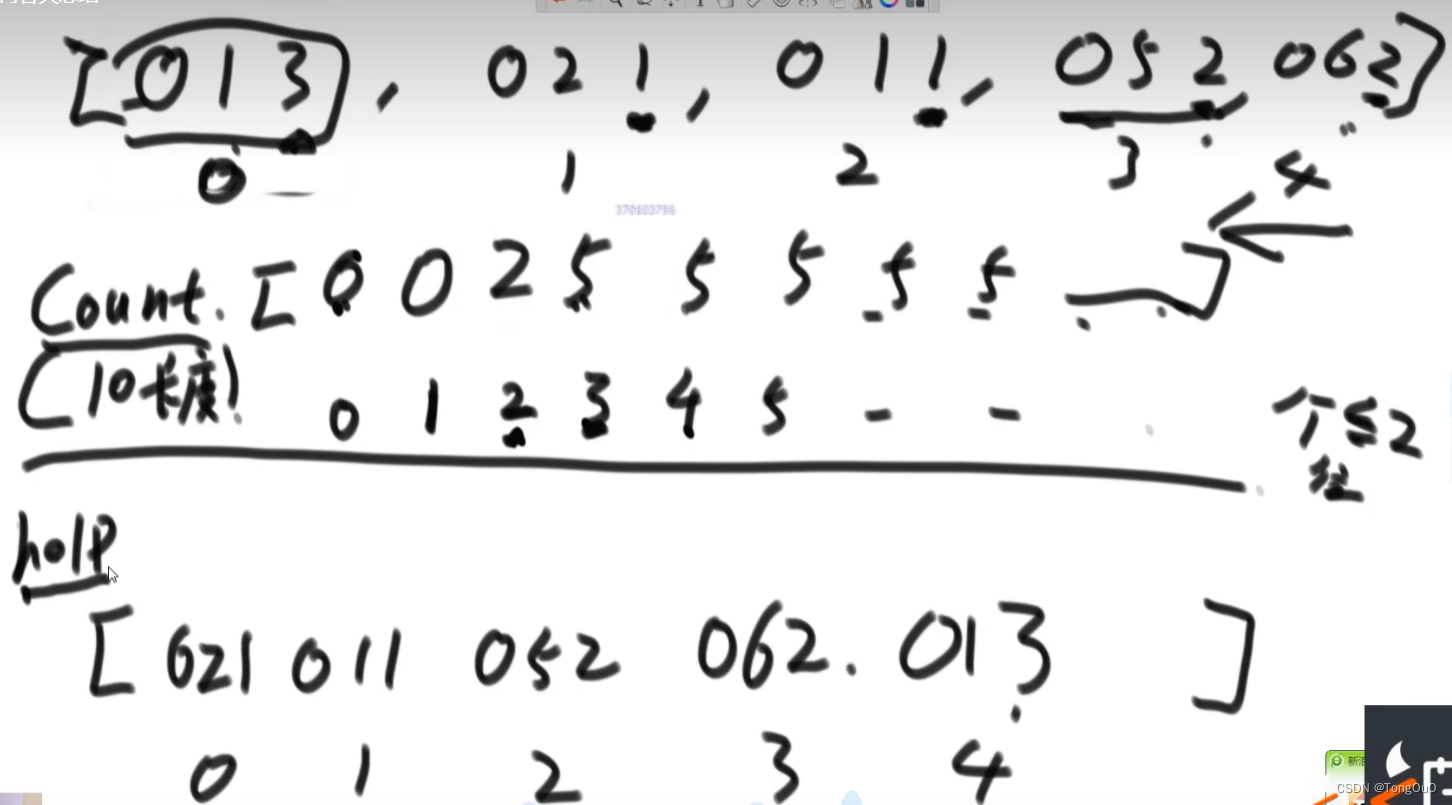
count为各位数字小于cout的有多少个,填在count减1的位置上面之后自身词频减一
代码实现:
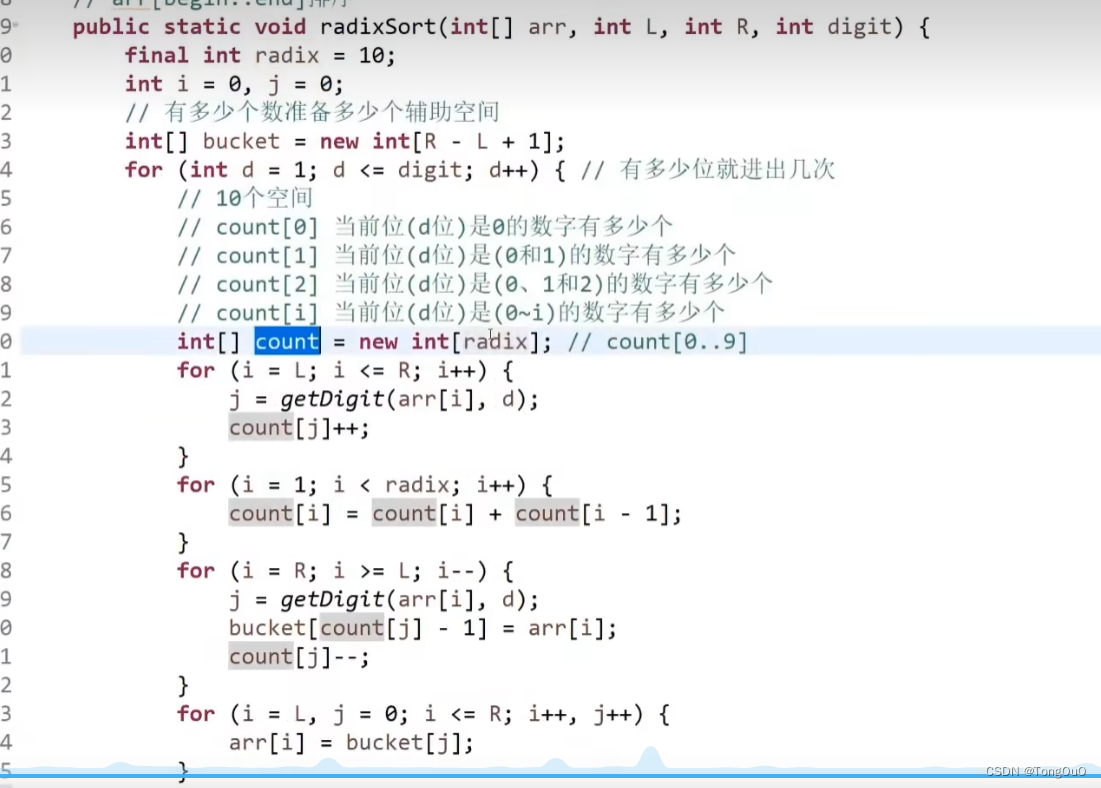
排序算法稳定性以及总结
稳定性

- 稳定性是指值相同的数字在排序完之后能否保证顺序不变
- 值相同的那些在排完序后仍能保持相对次序一样
- 对于基础类型没什么用,对于非基础类型比较有用
例如说先排年龄再排班级如果稳定的话就可以按照顺序排序了班级内的所有年龄人数
选择排序
做不到稳定
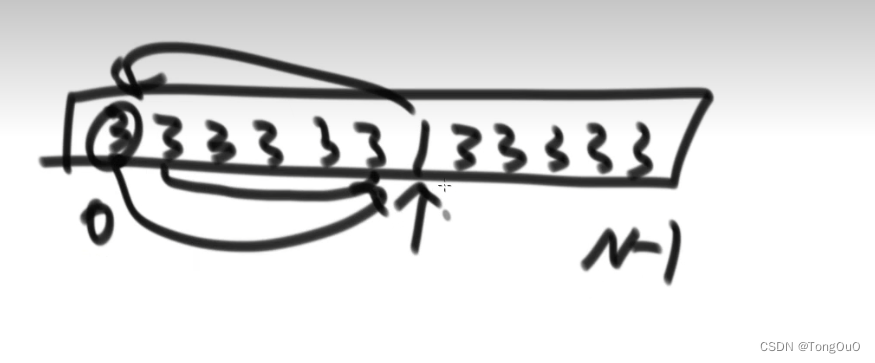 在全是3的数组中选一个移到前面就会破坏掉原有的3的结构
在全是3的数组中选一个移到前面就会破坏掉原有的3的结构
冒泡排序
冒泡排序可以,一直交换,相等的时候不换就可以保持稳定性
可以实现成稳定性
插入排序
可以实现稳定性,让每次右边的数大于等于左边的时候就停在右边,关键在于怎么处理相等的时候
归并排序
左侧和右侧相等我时候先考虑左边的就可以做到稳定了
所以也可以
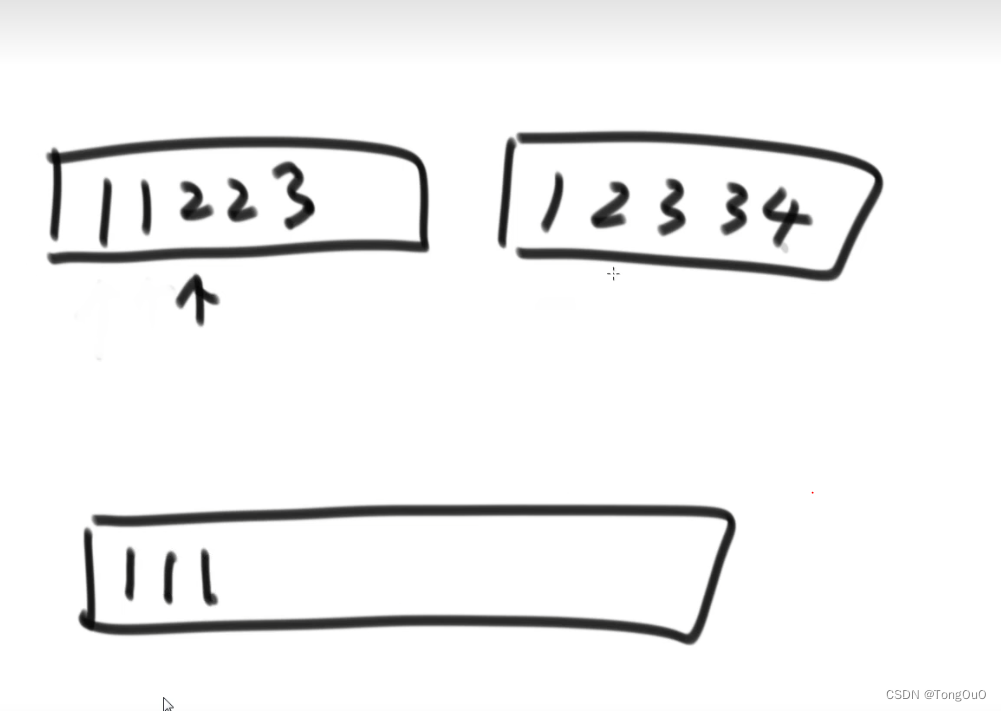
小和问题每次取右边的但同时会失去稳定性
快速排序
在partation时候做不到
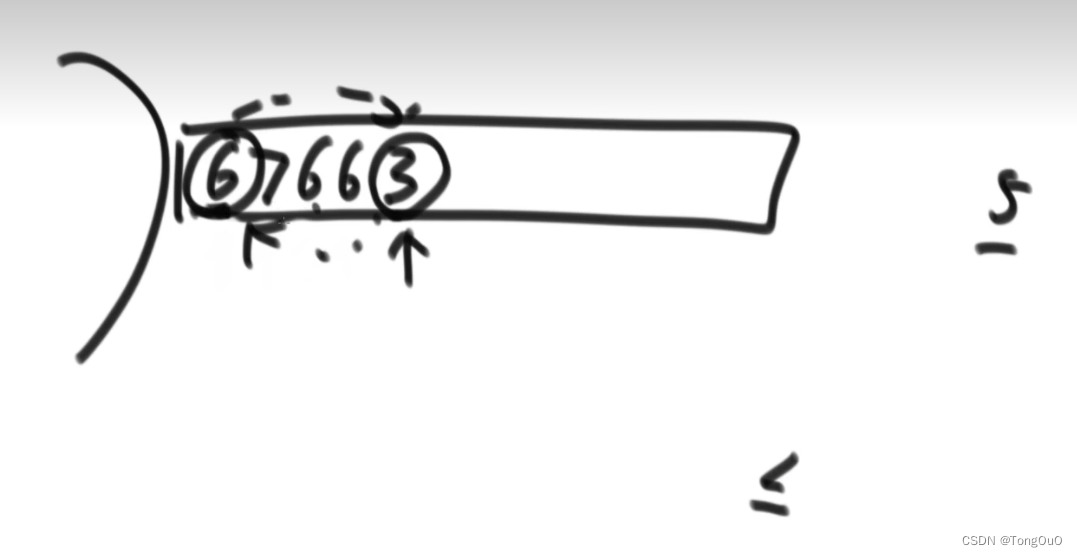
堆排序
在生成大根堆的时候就无法做到稳定性,在插入较大值到完全二叉树的左枝的时候就可以
计数排序和基数排序
都能做到稳定性,先入桶和先出通的东西都能做到稳定和比较无关都能很轻松做到稳定性
总结
