一、引入
采取一种更加一般的方法:

二、贪心选择性质
1、我们可以通过局部最优来构造整体最优解。
2、和动态规划的区别很明显,在动态规划中,每一个步骤都需要进行一次选择,而且选择依赖于子问题的解,因此,我们往往用一种自底向上的方式来解决动态规划问题(或者是带着备忘的自顶向下方法,当然,本质上还是需要先求解子问题再进行选择,还是自底向上);贪心算法中,我们只是选择眼前最好的,然后求解剩下的问题,在进行第一次选择之前是不求解任何子问题的,这个是彻彻底底的自顶向下,不断缩小问题。
3、贪心选择中有众多选择,我们需要改进以使它更加高效。
三、最优子结构
1、这个是能否应用动态规划和贪心算法的关键要素。
2、当应用于贪心算法时,我们通常使用更为直接的最优子结构。我们可以假定,通过对原问题应用贪心选择即可得到子问题。我们真正要做的全部工作就是论证:将子问题的最优解与贪心选择组合在一起就能生成原问题的最优解。这种方法隐含地对子问题使用了数学归纳法,证明了在每个步骤进行贪心选择会生成原问题的最优解。
1、贪心对动态规划

两个背包问题都具有最优子结构性质。对0-1背包问题,考虑重量不超过W而价值最高的装包方案。如果我们将商品j从此方案中删除,则剩余商品必须是重量不超过W-wj的价值最高的方案(小偷只能从不包括商品j的n-1个商品中选择拿走哪些)。
虽然两个问题相似,但我们用贪心策略可以求解分数背包问题,而不能求解0-1背包问题。
为了求解分数背包问题,我们首先计算每个商品的每磅价值vi/wi,遵循贪心策略,小偷首先尽量多地拿走每磅价值最高的商品。如果该商品已全部拿走而背包尚未满,他继续尽量多地拿走每磅价值第二高的商品,依此类推,直至达到重量上限W。因此,通过将商品按每磅价值排序,贪心算法的运行时间为O(n lgn)。
为什么贪心算法对0-1背包问题无效?
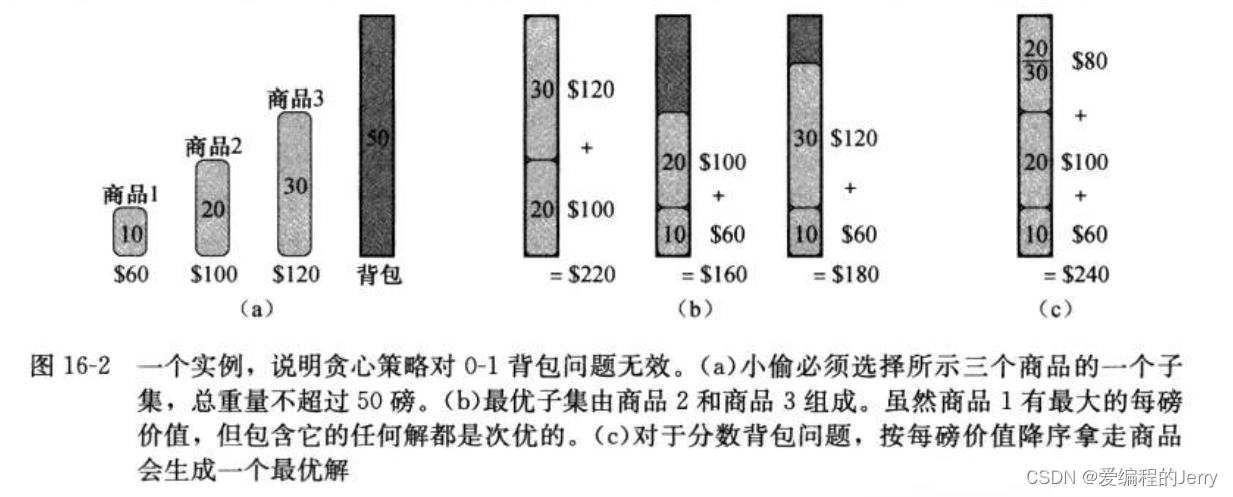
在0-1背包问题中,当我们考虑是否将一个商品装装入背包时,必须比较包含此商品的子问题的解与不包含它的子问题的解,然后才能做出选择。这会导致大量的重叠子问题——动态规划的标识。