二叉树
二叉树:一个节点的最大度为2
1. 节点的度:一个节点的子树个数
- 树的度:该树中最大的节点的度
- 节点的度为0—》叶子节点
- 节点的度不为0—》分支节点
2. 根节点:唯一一个没有父节点的节点
父节点
子节点
3.树中节点个数N和边数的关系:
边数=N-1;
4.节点的深度:当前节点到根节点的边长
树高度:最大的节点深度
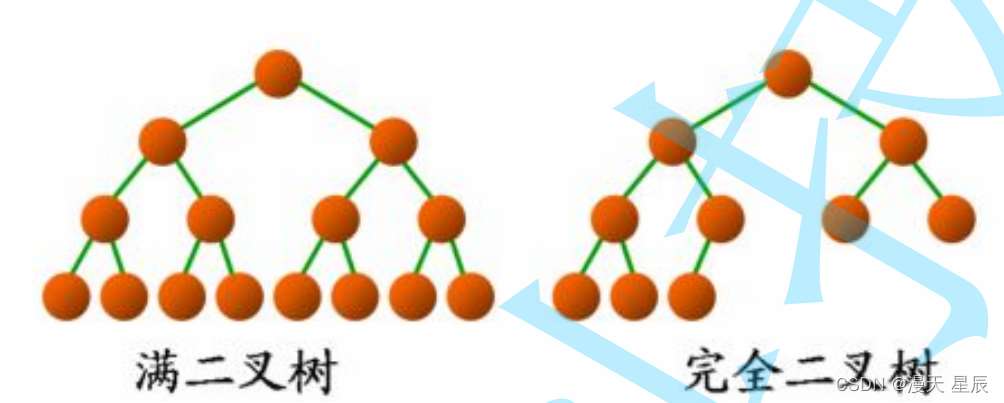
5. 满二叉树:特殊的完全二叉树,每个节点除了叶子节点外,度都是2
完全二叉树:一个节点若存在右数,则必然存在左数
节点个数N和树高度K
N=2^k-1
6.二叉树的性质
- 若根节点层数为1,则一颗非空二叉树的第i层上最多有2^(i-1)(i>0)个节点。
- 若规定只有根节点的二叉树的深度为1,则深度为K的二叉树的最大节点数是2^k - 1(k>=0)
- 对于任何一颗二叉树,如果其叶节点个数为n0,度为2的非叶节点个数为n2,则有 n0 = n2 +1。
重要4. 完全二叉树的编号问题
(1)若规定根节点编号为0,则对于一个节点为i的节点来说
左树节点编号为:2i+1
右树节点编号为:2i+2
父节点编号为(i-1)/2
二. 二叉树的存储
每个节点彼此之间如何互相访问
//孩子表示法
class Node{
int val;//数据域
Node left;//左孩子的引用,常常代表左孩子为根的整颗左子树
Node right;//右孩子的引用,常常代表右孩子为跟的整颗右子树
三. 二叉树的遍历
遍历:按照一定的顺序访问这个集合的所有元素,做到不重复,不遗漏。
能使用的递归的三个条件:
a.大问题能拆成小问题
b. 拆分后的问题和原问题除了数据大小不一样,解决思路完全一样。
c. 存在终止递归条件
跟;
先序(preOrder):跟左右
先访问根节点,再递归访问左子树,然后再递归访问右子树
中序(inOrder):左根右
先访递归问左子树,再访问根节点,然后再递归访问右子树
后序(postOrder):左右跟
先访递归问左子树,再递归访问右子树,然后再访问根节点
队列;
层序(levelOrder):按照树的深度一层层向下由左向右访问节点
结论:
- 先序遍历的第一个访问的是跟节点
后序遍历的最后一个访问的是根节点 - 中序和后序遍历的第一个节点是当前树的最左侧节点
- 针对中序遍历来说,左子树的遍历结果出现在根节点的左侧,右子树的遍历结果出现在根节点的右侧
- 给定二叉树的前中后序遍历结果,如何根据这三个结果确定二叉树结构