开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 力扣刷题笔记 -> 正文阅读

[数据结构与算法]力扣刷题笔记

力扣刷题

一、数组

1.二分法查找

适用场景：

数组按大小顺序排列
无重复值

形式：

[left,right]

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // 在左区间，所以[left, middle - 1]，且需要比较nums[middle],取right=middle-1
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

[left,right)

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);//>>等价于除2取左整数
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中，right取middle，即不去比较nums[middle]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

错误解法

int searchInsert(vector<int>& nums, int target) {
    int n = nums.size();
    int l = 0, r = n - 1;
    while (l <= r) {
        int mid = l + (r - l) / 2;
        if (nums[mid] > target)
            r = mid - 1;
        else
            l = mid;//由于除以2取左整数，导致l的值无法更新，因此会陷入死循环，破解方式为后面加个1
    }
    return l;
}

####注：

<<: 左移运算符，n<< m 相当于n乘以2的m次方
>>: 右移运算符，n >> m 相当于n除以2的m次方

2.双指针法

适用场景

思路：前后指针，数组复制

二、哈希表

Hash Tabel–散列表，哈希表，hash–n.搞砸。v.把…弄糟，反复推敲，剁碎
根据键（Key）而直接访问在内存存储位置的数据结构，通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

###1.判断一个数是否为快乐数：

难点

? 1. 求取数值各个位的平方和

? 2. unordered_set的应用

class Solution {
public:
    int getSum(int n)//求取数值各个位的平方和
    {
        int sum=0;
        while(n)
        {
            sum+=(n%10)*(n%10);
            n/=10;
        }
        return sum;
    }
    bool isHappy(int n) {
        unordered_set<int>set1;
        int numb=getSum(n);
        while(numb!=1)
        {
            if(set1.count(numb))
            {
                return false;
            }
            set1.insert(numb);
            numb=getSum(numb);
        }
        return true;
    }
};

2.查找两数之和

题目概述：在数组中找到和为目标值的两个数并返回下标
关键词：查找：当需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，首先想到用哈希法

? unordered_set与unordered_map底层实现都是哈希表，而unordered_map是key—value结构

? 返回下标：不仅要查找元素，还要返回其下标，则需要用key—value来存放元素

unordered_map常见用法

class Solution {
public:
  vector<int> twoSum(vector<int>& nums, int target) {
    unordered_map<int,int>map1;
    for(int i=0;i<nums.size();i++)
    {
      int a=target-nums[i];
      if(map1.find(a)==map1.end())
      {
        map1.insert(pair<int,int>(nums[i],i));
      }
      else
        return {map1.find(a)->second,i};
    }
    return {};
  }
};

3.查找四数之和（与四数之和同理）

题目概述：给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。

难点：降低时间复杂度和去重

双指针法：快慢指针，头尾指针

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>>fournumssum;
        sort(nums.begin(),nums.end());
        for(int i=0;i<nums.size();i++)
        {
            if(i>0&&nums[i]==nums[i-1])//剪枝操作
                continue;       
            for(int j=i+1;j<nums.size();j++)
            {
                if(j>i+1&&nums[j]==nums[j-1])//二次剪枝
                    continue;
                int left=j+1;
                int right=nums.size()-1;  
                while(left<right)
                {
                    if((long)nums[i]+nums[j]+nums[left]+nums[right]>target)
                        right--;
                    else if((long)nums[i]+nums[j]+nums[left]+nums[right]<target)
                        left++;
                    else
                    {
                        fournumssum.push_back({nums[i],nums[j],nums[left],nums[right]});
                        while(left<right&&nums[left]==nums[left+1])
                            left++;
                        while(left<right&&nums[right]==nums[right-1])  
                            right--; 
                        right--;
                        left++;     
                    }  
                }     
            }
        }
        return fournumssum;
    }
};

三、链表

注意点

设置虚拟头节点可以省去很多麻烦，但在程序结束时最好将其释放
单链表中很多操作需要设置临时节点用以保存某些节点
注意操作顺序，如力扣24题交换相邻节点时，改变指向时要遵循链表读取顺序

24.两两交换链表的相邻节点

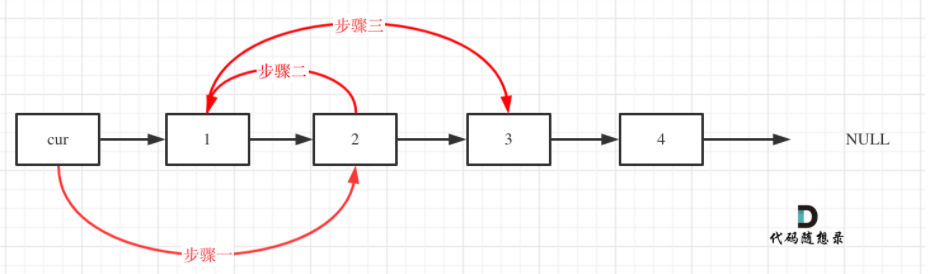
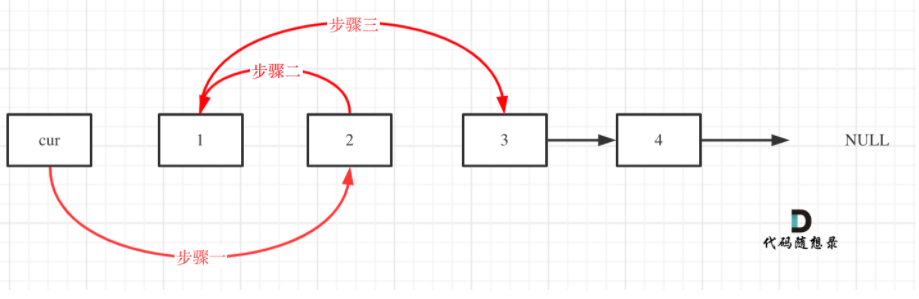
即：

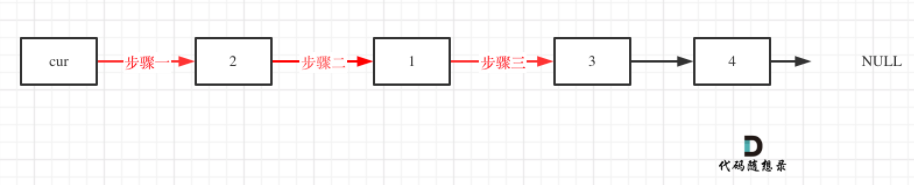
注意：

顺序变换遵循单链表的遍历顺序，用临时指针保存节点，操作完成后释放虚拟头节点的内存区域

class Solution {

public:

  ListNode* swapPairs(ListNode* head) {
    ListNode *dummyhead=new ListNode(0);
    dummyhead->next=head;
    ListNode* cur=dummyhead;
    while(cur->next!=NULL&&cur->next->next!=NULL)
    {
      ListNode* temp1=cur->next;
      ListNode* temp2=cur->next->next->next;
      cur->next=cur->next->next;
      cur->next->next=temp1;
      temp1->next=temp2;
      cur=cur->next->next;
    }
    ListNode* temp=dummyhead->next;
    delete dummyhead;
    return temp;
  }
};

四、字符串

1.反转字符串

方法：双指针
交换两数不用中间变量的方法
```
a=a^b;
b=a^b;
a=a^b;
```

2.反转字符串中的单词

思路：删除多余空格->翻转整个字符串->翻转单个单词

难点：删除多余空格（移除多余元素，注意时间复杂度），翻转单个单词

删除多余空格（快慢指针）

法一：去前->去中->去尾

//版本一 
void removeExtraSpaces(string& s) {
    int slowIndex = 0, fastIndex = 0; // 定义快指针，慢指针
    // 去掉字符串前面的空格
    while (s.size() > 0 && fastIndex < s.size() && s[fastIndex] == ' ') {
        fastIndex++;
    }
    for (; fastIndex < s.size(); fastIndex++) {
        // 去掉字符串中间部分的冗余空格
        if (fastIndex - 1 > 0
                && s[fastIndex - 1] == s[fastIndex]
                && s[fastIndex] == ' ') {
            continue;
        } else {
            s[slowIndex++] = s[fastIndex];
        }
    }
    if (slowIndex - 1 > 0 && s[slowIndex - 1] == ' ') { // 去掉字符串末尾的空格
        s.resize(slowIndex - 1);
    } else {
        s.resize(slowIndex); // 重新设置字符串大小
    }
}

法2：

// 版本二 
void removeExtraSpaces(string& s) {//去除所有空格并在相邻单词之间添加空格, 快慢指针。
    int slow = 0;   //整体思想参考https://programmercarl.com/0027.移除元素.html
    for (int i = 0; i < s.size(); ++i) { //
        if (s[i] != ' ') { //遇到非空格就处理，即删除所有空格。
            if (slow != 0) s[slow++] = ' '; //手动控制空格，给单词之间添加空格。slow != 0说明不是第一个单词，需要在单词前添加空格。
            while (i < s.size() && s[i] != ' ') { //补上该单词，遇到空格说明单词结束。
                s[slow++] = s[i++];
            }
        }
    }
    s.resize(slow); //slow的大小即为去除多余空格后的大小。
}

3.实现strStr()函数

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

关键点：记录位置，降低复杂度

双指针解法：

class Solution {
public:
    int strStr(string haystack, string needle) {

        int rtnnum=-1;
        for(int i=0,j=0;i<haystack.size();)
        {
            if(haystack[i+j]==needle[j])//逐个比对
            {
                j++;//j指向模式串
            }
            else
            {
                i++;//继续向下对比
                j=0;//返回模式串初始位置
            }
            if(j==needle.size())//全部比对完成
            {
                return i;
                break;
            }
        }
        return rtnnum;
    }
};

暴力解法：

class Solution {
public:
    int strStr(string haystack, string needle) {
        return haystack.find(needle);
    }
};//哈哈哈

KMP算法（暂时不会）

文本串

模式串需要有一定对称性

前缀：包含首字母不包含尾字母的子字符串（从左往右），如aabaaf的前缀有a,aa,aab,aaba,aabaa,。后缀同理

前缀表：(相等前后缀数量？)

a	a	b	a	a	f
0	1	0	1	2	0

next数组求法：

初始化-》处理前后缀不相同的情况-》处理前后缀相同的情况

i指向后缀末尾，j指向与后缀相同的最长前缀末尾（其实整体减一更容易理解

void getNext(int* next, const string& s){//减1实现
    int j = -1;
    next[0] = j;
    for(int i = 1; i < s.size(); i++) { // 注意i从1开始
        while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
            j = next[j]; // 向前回退
        }
        if (s[i] == s[j + 1]) { // 找到相同的前后缀
            j++;
        }
        next[i] = j; // 将j（前缀的长度）赋给next[i]
    }
}

void getNext(int* next, const string& s) {//不减1实现
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
}

五、栈和队列

栈是容器适配器，底层容器使用不同的容器，导致栈内数据在内存中不是连续分布。

缺省情况（构造函数缺省）下默认底层容器是deque(双向队列)，其在内存中的数据分布也是不连续的。

###1.用栈（stack）实现队列（queue）

栈的特点：先入后出

队列的特点：先入先出

要想用栈实现队列，需要用两个栈来维护入队何出队顺序。入队时，进入stIn，出队时，当stOut不为空时只需从stOut出，若为空，则需要将stIn依次全部转移到stOut中，以此保证队列先进先出的特点。

class MyQueue {
public:
    stack<int> stIn;
    stack<int> stOut;
    /** Initialize your data structure here. */
    MyQueue() {

    }
    /** Push element x to the back of queue. */
    void push(int x) {
        stIn.push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        // 只有当stOut为空的时候，再从stIn里导入数据（导入stIn全部数据）
        if (stOut.empty()) {
            // 从stIn导入数据直到stIn为空
            while(!stIn.empty()) {
                stOut.push(stIn.top());
                stIn.pop();
            }
        }
        int result = stOut.top();
        stOut.pop();
        return result;
    }
    
    /** Get the front element. */
    int fornt() {
        int res = this->pop(); // 直接使用已有的pop函数
        stOut.push(res); // 因为pop函数弹出了元素res，所以再添加回去
        return res;
    }
    
    /** Returns whether the queue is empty. */
    bool empty() {
        return stIn.empty() && stOut.empty();
    }

};

2.用队列实现栈

方法一：用两个队列，一个作为出栈时的辅助队列

思路：入栈时，进入qIn队列；出栈时，此时要出栈的元素在qIn队尾，要想将其取出，需要将qIn中除此元素的所有队前元素全部依次转移至qOut队列中，交换两个队列后qOut队头即为要出栈的元素。再从qOut出队。（或者第二个队列看作备份队列，出栈时先将除要出栈元素以外的元素依次转移至备份队列中，将该元素出队后将q2赋值给q1）

class MyStack {
public:
    queue<int> que1;
    queue<int> que2; // 辅助队列，用来备份
    /** Initialize your data structure here. */
    MyStack() {
    }
    
    /** Push element x onto stack. */
    void push(int x) {
        que1.push(x);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        int size = que1.size();
        size--;
        while (size--) { // 将que1 导入que2，但要留下最后一个元素
            que2.push(que1.front());
            que1.pop();
        }
    
        int result = que1.front(); // 留下的最后一个元素就是要返回的值
        que1.pop();
        que1 = que2;            // 再将que2赋值给que1
        while (!que2.empty()) { // 清空que2
            que2.pop();
        }
        return result;
    }
    
    /** Get the top element. */
    int top() {
        return que1.back();
    }
    
    /** Returns whether the stack is empty. */
    bool empty() {
        return que1.empty();
    }
};

方法2：一个队列实现

思路：入栈即入队，出栈时，将除出栈元素之外的所有元素移动至队尾，此时队头即为要出栈的元素

class MyStack {
public:
    queue<int> que;
    /** Initialize your data structure here. */
    MyStack() {

    }
    /** Push element x onto stack. */
    void push(int x) {
        que.push(x);
    }
    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        int size = que.size();
        size--;
        while (size--) { // 将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部
            que.push(que.front());
            que.pop();
        }
        int result = que.front(); // 此时弹出的元素顺序就是栈的顺序了
        que.pop();
        return result;
    }
    
    /** Get the top element. */
    int top() {
        return que.back();
    }
    
    /** Returns whether the stack is empty. */
    bool empty() {
        return que.empty();
    }
};

4.逆波兰表达式求值

逆波兰表达式：运算符前的两个元素相运算获得一个元素。若为数字则入栈，若为运算符则出栈两个元素，运算结果入栈。stoi(s)，字符串转数字

5.滑动窗口最大值

若使用暴力解法，需要找出每个滑动窗口的最大值，时间复杂度：O（n*k）。

大顶堆确实可以弹出最大值，但却无法弹出其他值，导致其维护的不是滑动窗口内的数值。

用单调队列：

copy某评论：单调队列真是一种让人感到五味杂陈的数据结构，它的维护过程更是如此…就拿此题来说，队头最大，往队尾方向单调…有机会站在队头的老大永远心狠手辣，当它从队尾杀进去的时候，如果它发现这里面没一个够自己打的，它会毫无人性地屠城，把原先队里的人头全部丢出去，转身建立起自己的政权，野心勃勃地准备开创一个新的王朝…这时候，它的人格竟发生了一百八十度大反转，它变成了一位胸怀宽广的慈父！它热情地请那些新来的“小个子”们入住自己的王国…然而，这些小个子似乎天性都是一样的——嫉妒心强，倘若见到比自己还小的居然更早入住王国，它们会心狠手辣地找一个夜晚把它们通通干掉，好让自己享受更大的“蛋糕”；当然，遇到比自己强大的，它们也没辙，乖乖夹起尾巴做人。像这样的暗杀事件每天都在上演，虽然王国里日益笼罩上白色恐怖，但是好在没有后来者强大到足以干翻国王，江山还算能稳住。直到有一天，闯进来了一位真正厉害的角色，就像当年打江山的国王一样，手段狠辣，野心膨胀，于是又是大屠城…历史总是轮回的。

class Solution {
public:
    class myque{
        public:
            deque<int>que;
            void push(int value)
            {
                while(!que.empty()&&value>que.back())
                    que.pop_back();
                que.push_back(value);
            }
            void pop(int value)
            {
                if(!que.empty()&&value==que.front())//若滑动窗口左端值正好为最大值，就得pop掉
                    que.pop_front();
            }
            int getmax()
            {
                return que.front();
            }
    };
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        myque que;
        vector<int>result;
        for(int i=0;i<k;i++)
        {
            que.push(nums[i]);
        }
        result.push_back(que.getmax());
        for(int i=k;i<nums.size();i++)
        {
            que.pop(nums[i-k]);
            que.push(nums[i]);
            result.push_back(que.getmax());
        }
        return result;
    }
};

6.前k个高频元素

大顶堆与小顶堆的概念

顶堆：披着优先级队列外衣的堆

大顶堆：最大的元素永远在上面
小顶堆：参照大顶堆

    // 小顶堆
    class mycomparison {//如果是非基本数据类型，就得重写仿函数，确定比较方式，也可以重载<或者>
    public:
        bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
            return lhs.second > rhs.second;
        }
    };
    // 定义一个小顶堆，大小为k
    priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;

优先队列有三个参数，其声明式为：

priority_queue< type, container, function >

这三个参数，后面两个可以省略，第一个不可以。其中：
**type：**数据类型；
**container：**实现优先队列的底层容器；
**function：**元素之间的比较方式；
对于container，要求必须是数组形式实现的容器，例如vector、deque，而不能使list。
在STL中，默认情况下（不加后面两个参数）是以vector为容器，以 operator< 为比较方式，所以在只使用第一个参数时，优先队列默认是一个最大堆，每次输出的堆顶元素是此时堆中的最大元素。

六、二叉树

1.递归

递归思想：以小见大（把规模大的问题转化为规模小的相似的子问题来解决），递去归来
递归三要素

1、明确递归终止条件； 2、给出递归终止时的处理办法； 3、提取重复的逻辑，缩小问题规模。
应用场景

? (1). 问题的定义是按递归定义的（Fibonacci函数，阶乘，…）；

(2). 问题的解法是递归的（有些问题只能使用递归方法来解决，例如，汉诺塔问题，…）；

(3). 数据结构是递归的（链表、树等的操作，包括树的遍历，树的深度，…）。

在求解规模不确定的情况下，由于函数调用的开销，递归常常会带来性能问题

2.深度优先与广度优先

深度优先：用递归和迭代（用栈操作）
广度优先：用递归和迭代（队列操作）

3 .二叉树顺序遍历

递归遍历(深层思想也是栈，因为递归能干的栈也能干)

void trversal(vector<int>&result,TreeNode* cur)//前序遍历递归法，确定返回值和参数列表
{
    if(cur==NULL)return;//确定结束条件
    result.push_back(cur->val);//根
    trversal(result,cur->left);//左
    trversal(result,cur->right);//右 
}

迭代遍历（栈的思想）

vector<int> preorderTraversal(TreeNode* root) //前序遍历
{
    vector<int>result;
    stack<TreeNode*>st;
    TreeNode* cur=root;
    st.push(cur);
    if(cur==NULL)return;
    while(!st.empty())
    {
        cur=cur.top();
        result.push_back(cur->val);//根
        st.pop();
        if(cur->right)st.push(cur->right);//右
        if(cur->left)st.push(cur->left);//左
    }
}

vector<int> preorderTraversal(TreeNode* root) //中序遍历，与前序遍历思路不太一样
{
    vector<int>result;
    stack<TreeNode*>st;
    TreeNode* cur=root;
    st.push(cur);
    if(cur==NULL)return;
    while(!st.empty())
    {
        cur=cur.top();
        result.push_back(cur->val);//根
        st.pop();
        if(cur->right)st.push(cur->right);//右，注意入栈条件
        if(cur->left)st.push(cur->left);//左
    }
}

###3.二叉树层序遍历（深度优先遍历）

递归遍历

    void order(TreeNode* cur, vector<vector<int>>& result, int depth)//确定返回值和参数列表
    {
        if (cur == nullptr) return;
        if (result.size() == depth) result.push_back(vector<int>());//若该层无容器（表现为深度==二维容器大小），则放入个容器
        result[depth].push_back(cur->val);//把当前节点放入对应层中
        order(cur->left, result, depth + 1);//深度递增，从左到右
        order(cur->right, result, depth + 1);
    }

迭代遍历（队列实现）

思想：将出队元素的左右子入队

    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);//注意入栈条件
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }

;//深度递增，从左到右
order(cur->right, result, depth + 1);
}


- 迭代遍历（队列实现）

  思想：将出队元素的左右子入队

```C++
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);//注意入栈条件
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }