[数据结构与算法]（C语言）数据结构——排序算法总结与比较

目录

• 一、排序的概念及其运用
• • 排序的概念
• 二、插入排序
• • 直接插入排序：
  • 希尔排序：
• 三、选择排序
• • 直接选择排序：
  • 堆排序：
• 四、交换排序
• • 冒泡排序：
  • 快速排序：
• 五、归并排序

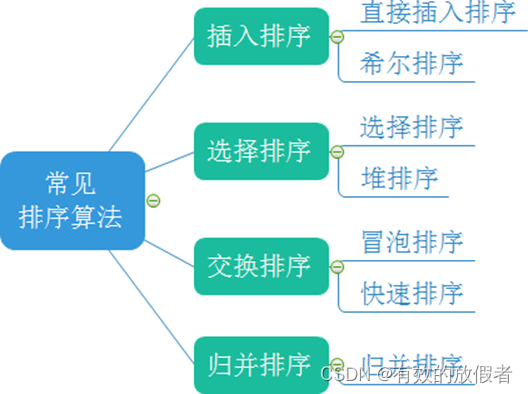
一、排序的概念及其运用

排序的概念

• 排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
• 稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
  有些排序算法无论如何都不能保证它是稳定的，那么它就是不稳定的
  但有些排序算法我们加以控制就可以保证他是稳定的，那么它就是稳定的
• 内部排序：数据元素全部放在内存中的排序。
• 外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

二、插入排序

详细博客链接：插入排序

直接插入排序：

• 时间复杂度（最坏）：O($n^2$)
  解释：第一次最坏移动一次元素，第二次最坏移动两次元素，以此类推，第n次最坏移动n次元素，所以计算公式为$(1+n)?n/2$近似等于O($n^2$)
• 空间复杂度：O(1)
• 稳定性：稳定
• 初始数据集的排列顺序对算法的性能有无影响：有影响。
  解释：有序的情况下就不需要往前移动元素了，但是整趟排序最好的情况下外面的for循环也要进行n次。

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)//整趟排序的循环
	{
		int end = i;
		int tmp = a[end + 1];

		while (end >= 0)//让循环停止的条件有两个，一个是end<0,另一个是a[end] <= tmp
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];//往后挪元素
				end--;
			}
			else
			{
				break;//有序的情况下这里提前break退出循环
			}
		}
		a[end + 1] = tmp;//上面循环停止时在end+1的位置赋值为tmp即可
	}
}

希尔排序：

• 时间复杂度（最坏）：约为O($n^{1.3}$)

• 空间复杂度：O(1)

• 稳定性：稳定

• 初始数据集的排列顺序对算法的性能有无影响：有影响。
  解释：希尔是对插入排序的优化，这种优化是在无序的序列中才有明显的效果，如果序列接近有序，反而是插入最优。

三、选择排序

详细博客链接：选择排序

直接选择排序：

• 时间复杂度（最坏）：O($n^2$)
• 空间复杂度：O(1)
• 稳定性：不稳定
• 初始数据集的排列顺序对算法的性能有无影响：没有影响。
  解释：无论有序还是无序，都要全部进行比较。

堆排序：

• 时间复杂度（最坏）：O($n?lo{g}_2^n$)
• 解释：n是建堆的时间，$lo{g}_2^n$是在堆中查找的时间
• 空间复杂度：O(1)
• 稳定性：不稳定
• 初始数据集的排列顺序对算法的性能有无影响：没有影响。
  解释：雷打不动的就是一直排序到最后一个元素，无论有序还是无序。

四、交换排序

详细博客链接：（C语言）数据结构——冒泡排序和快速排序（超详解）

冒泡排序：

• 时间复杂度（最坏）：O($n^2$)
• 空间复杂度：O(1)
• 稳定性：稳定
• 初始数据集的排列顺序对算法的性能有无影响：有影响。
  解释：我们可以设置一个flag，若一趟排序中没有数据交换的情况下，根据flag的值就可以控制结束整个程序的进行。

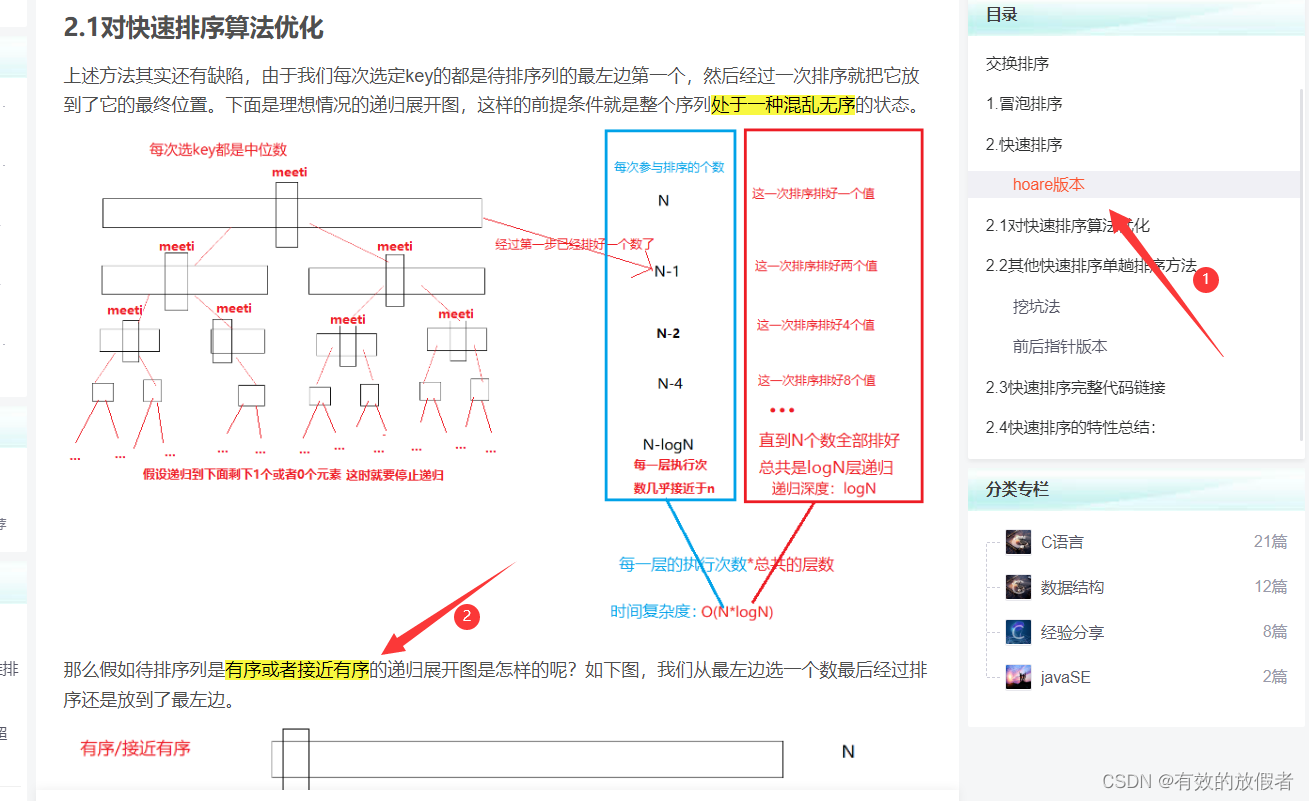
快速排序：

• 时间复杂度（优化过后）：O($n?lo{g}_2^n$)
• 空间复杂度：O($lo{g}_2^n$)
  解释：递归一边（左边）建立了$lo{g}_2^n$层栈帧，退回去再调用另一边（右边），用的是之前的空间。
• 稳定性：不稳定
  解释：举个例子，假如全是相同的元素的时候，必然中间的那个值会被替换成为基准值key
• 初始数据集的排列顺序对算法的性能有无影响：有影响。
  解释：详情可以参考（C语言）数据结构——冒泡排序和快速排序（超详解）中对快速排序算法的优化，会给你一些启发
  

五、归并排序

博客链接：归并排序

• 时间复杂度（最坏）：O($n?lo{g}_2^n$)
• 空间复杂度：O(n)
• 稳定性：稳定
  解释：下面递归的代码，加上一个等于号，我们就能控制它是稳定的。
  看下面代码：

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin == end)
		return;

	int mid = (end + begin) / 2;
	// [begin, mid] [mid+1, end]

	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid+1, end, tmp);

	// 取小的尾插
	// [begin, mid] [mid+1, end]
	int begin1 = begin, end1 = mid;
	int begin2 = mid+1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])///把这里的等于号去掉就不是稳定的了
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	// 拷贝回原数组 -- 归并哪部分就拷贝哪部分回去
	memcpy(a+begin, tmp+begin, (end-begin+1)*sizeof(int));
}

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	_MergeSort(a, 0, n - 1, tmp);

	free(tmp);
	tmp = NULL;
}

• 初始数据集的排列顺序对算法的性能有无影响：没有影响。

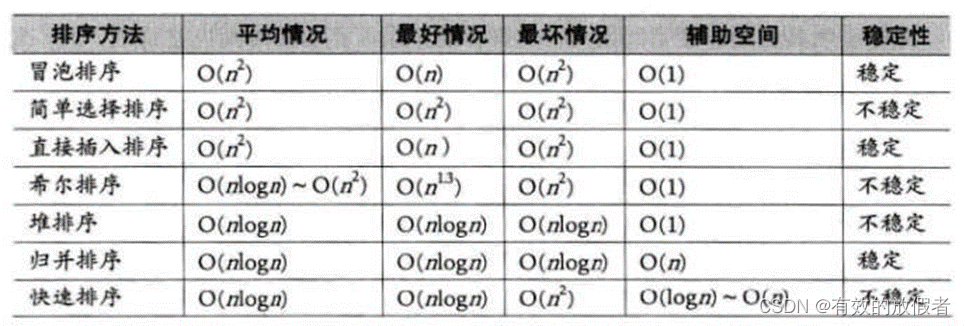
总结：

end
有哪里看不懂可以随时向博主提问
有错误的地方欢迎各位老铁批评指正。