开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 数据结构：哈希表——线性探测哈希表、链式哈希表的实现 -> 正文阅读

[数据结构与算法]数据结构：哈希表——线性探测哈希表、链式哈希表的实现

前言

在C++的STL中，
有序关联容器有 set、map，他们的底层实现是红黑树，查询时间是O(logn)；
无需关联容器有 unordered_set、unordered_map，他们的底层实现是哈希表，均摊查询时间为O(1)。

散列表/哈希表定义

使关键字和其存储位置满足关系：存储位置 = f（关键字），这就是一种新的存储技术-散列技术。
散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f，使得每个关键字key对应一个存储位置f（key），在查找时，根据这个确定的对应关系找到给定key的映射f(key)，如果待查找集合中存在这个记录，则必定在f（key）的位置上。
我们把这种对应关系f称为散列函数，又称为哈希函数。采用散列技术将记录存储在一块连续的存储空间中，这块连续的存储空间称为散列表或者哈希表（Hash Table）。

散列函数

元素的值通过一个映射关系得到元素在表中的存储位置，这张表就可以叫做散列表或哈希表。

简单示例：
直接映射：
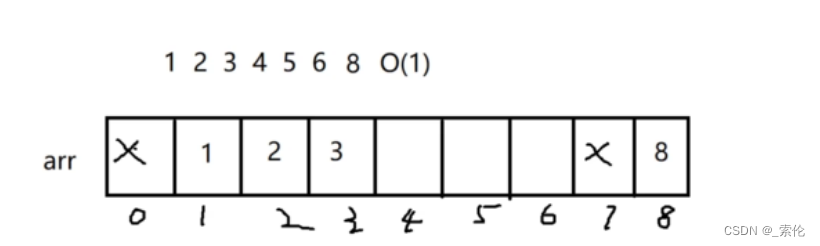
有一组元素，把他们当作下标存储到数组内，数组首先初始化为-1，那么在查询时候，若int val = 3, arr[val] == -1则 3不存在，arr[val] ==3，则3存在。

在这里插入图片描述

除留余数法

像上面的直接映射，会面临一些问题，如果数据差距过大，如：[1, 2, 100000]，那么直接映射需要申请巨大的空间，造成浪费。

所以这里介绍一个哈希函数：除留余数法

比如：
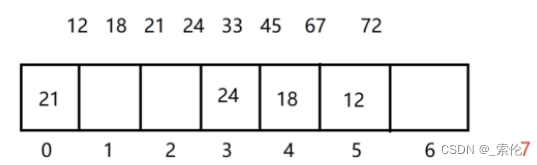
12 % 7 = 5，那么把12放到5号元素
18 % 7 = 4，18放到4号元素
21 % 7 = 0， 21放到0号元素
…
33 % 7 = 5，这时候就产生了一个问题，即该位置已经被占用，这种情况叫做【哈希冲突/哈希碰撞】。

在这里插入图片描述

哈希冲突解决方法

1. 线性探测法
2. 链地址法

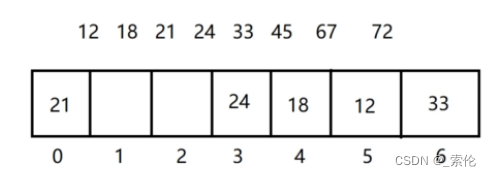
线性探测法：当该位置被占用时，继续往后找空的位置，如图，33本该放在5号元素，被占用的话往后找，6号元素为空，则占用6号元素。

在这里插入图片描述

下一个数字45 % 7 = 3，也需要线性探测，后面都被占用，那么需要从头开始找空闲位置。
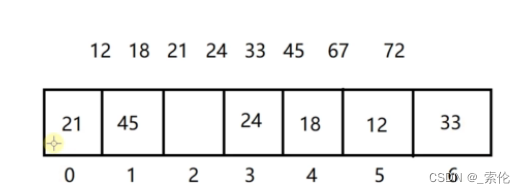
在这里插入图片描述

那么这时候又会有一个问题，我们使用哈希表是因为它的增加和查询效率为O(1)，如果像上面这样，产生哈希冲突次数很多的话，那么会导致它的增加、查询、删除操作的时间复杂度从O(1)趋向于O(n）。

除留余数法的优化

哈希表的长度取素数，这样取模操作，哈希冲突概率会下降。
哈希表的装载因子 loadFactor：已占有的桶的个数 / 桶的总个数。一般取值0.75。如果装载因子大于该值，那么直接对哈希表扩容，对原数据重新哈希，减少哈希冲突。

线性探测哈希表的实现

哈希表的设计

首先可以对每个桶设计一个状态，表示当前桶是否被使用：

// 桶状态
enum State
{
	STATE_UNUSE,	// 从未使用过的桶
	STATE_USING,	// 正在使用中
	STATE_DEL,		// 删除过元素的桶
};

桶的类型：

// 桶的类型
struct Bucket
{
	Bucket(int key = 0, State state = STATE_UNUSE)
		: key_(key)
		, state_(state)
	{}

	int key_;		// 存储的数据
	State state_;	// 桶的当前状态
};

哈希表的数据成员：

class HashTable
{
private:
	Bucket* table_;		// 指向动态开辟的哈希表
	int tableSize_;		// 哈希表当前的长度
	int useBucketNum_;	// 已使用的桶的个数

	double loadFactor_;	// 哈希表的装载因子

	static const int PRIME_SIZE = 10; // 素数表的大小
	static int primes_[PRIME_SIZE];	// 素数表
	int primeIdx_;		// 当前素数表的下标
};
int HashTable::primes_[HashTable::PRIME_SIZE] = { 3, 7, 23, 47, 97, 251, 443, 991, 1471, 42773 };

构造函数

默认传入初始化表的大小和装载因子，首先把传入的表的大小初始化为接近的素数（素数可以降低哈希冲突概率），如果下标超过了素数表的大小，那么就把哈希表大小置为素数表最后一位元素大小。

HashTable(int size = primes_[0], double loadFactor = 0.75)
	: useBucketNum_(0)
	, loadFactor_(loadFactor)
	, primeIdx_(0)
{
	// 吧用户传入的size调整到最近的比较大的素数上
	if (size != primes_[0])
	{
		for (; primeIdx_ < PRIME_SIZE; ++primeIdx_)
		{
			if (primes_[primeIdx_] > size)
				break;
		}

		// 用户传入的哈希size过大，已超过最后一个素数，则
		// 调整到最后一个素数
		if (primeIdx_ == PRIME_SIZE)
		{
			primeIdx_--;
		}
	}

	tableSize_ = primes_[primeIdx_];
	table_ = new Bucket[tableSize_];
}

析构函数

~HashTable()
{
	delete[]table_;
	table_ = nullptr;
}

那么在增删查操作时，各自的步骤为：

增加-insert()

通过哈希函数计算数据存放的位置；若该位置状态显示空闲，则直接存储元素，返回；若该位置状态为被占用，则从当前位置向后找空闲位置。

每次进来，先考虑扩容，即装载因子超过0.75，就扩容

bool insert(int key)
{
	// 首先考虑是否需要扩容,计算装载因子
	double factor = useBucketNum_ * 1.0 / tableSize_;
	cout << "factor: " << factor << endl;
	if (factor > loadFactor_)
	{
		// 开始扩容
		expand();
	}
		
	int idx = key % tableSize_;
	int i = idx;
	do
	{
		if (table_[i].state_ != STATE_USING)
		{
			table_[i].state_ = STATE_USING;
			table_[i].key_ = key;
			useBucketNum_++;
			return true;
		}
		i = (i + 1) % tableSize_;
	} while (i != idx);
		
	/*
	* 这段代码是刚开始写的，发现可以用do...while()代替
	* 
	// 如果当前位置没有使用，则使用该位置
	if (table_[idx].state_ != STATE_USING)
	{
		table_[idx].state_ = STATE_USING;
		table_[idx].key_ = key;
		return true;
	}

	// 如果上面条件没返回，那么就说明产生哈希冲突，进行线性探测
	for (int i = (idx + 1) % tableSize_; i != idx; i = (i + 1) % tableSize_)
	{
		if (table_[i].state_ != STATE_USING)
		{
			table_[i].state_ = STATE_USING;
			table_[i].key_ = key;
			return true;
		}
	}
	*/

	return false;
}

查询-find()

通过哈希函数计算数据存放的位置，从该位置取值，该值等于要查询的元素值，则找到；该值不等于要查询的元素值，继续往后遍历。

// 查询元素
bool find(int key) const
{
	int idx = key % tableSize_;
	int i = idx;

	do
	{
		// 如果合法，且值相等
		if (table_[i].state_ == STATE_USING && table_[i].key_ == key)
		{
			return true;
		}
		i = (i + 1) % tableSize_;
	} while (table_[i].state_ != STATE_UNUSE && i != idx);

	return false;
}

删除-erase()

通过哈希函数计算数据存放的位置，从该位置取值，判断状态STATE_USING，该值等于要删除的值，则只修改当前位置的状态，改成STATE_DEL；若该值不等于要删除的值，从当前位置向后遍历，修改状态，如果遇到STATE_UNUSE，说明可以结束了，因为哈希冲突没有到达这个地方。

// 删除元素
bool erase(int key)
{
	int idx = key % tableSize_;
	int i = idx;

	do
	{
		// 如果合法，且值相等
		if (table_[i].state_ == STATE_USING && table_[i].key_ == key)
		{
			table_[i].state_ = STATE_DEL;
			useBucketNum_--;
		}
		i = (i + 1) % tableSize_;
	} while (table_[i].state_ != STATE_UNUSE && i != idx);

	return true;
}

扩容-expand()

首先对哈希数组扩容，扩容大小根据素数表；然后遍历旧的哈希表，对于被占用的桶，取出有效数据，重新哈希到新的表中；再delete掉旧的表，让旧的指针指向新表。

// 扩容
void expand()
{
	++primeIdx_;
	if (primeIdx_ == PRIME_SIZE)
	{
		throw "HashTable is too large, can't expand anymore!";
	}

	// 申请新的哈希表
	Bucket* newTable = new Bucket[primes_[primeIdx_]];

	// 遍历原来哈希表,判断存储过值的桶
	for (int i = 0; i < tableSize_; ++i)
	{
		// 找到旧表有效的数据，重新哈希到新表中
		if (table_[i].state_ == STATE_USING)
		{
			int idx = table_[i].key_ % primes_[primeIdx_];
			int k = idx;

			do
			{
				if (newTable[k].state_ != STATE_USING)
				{
					newTable[k].state_ = STATE_USING;
					newTable[k].key_ = table_[i].key_;
					break;
				}
				k = (k + 1) % primes_[primeIdx_];
			} while (k != idx);
		}
	}

	delete[]table_;
	table_ = newTable;
	tableSize_ = primes_[primeIdx_];
}

链式哈希表的实现

在上面所说的线性探测哈希表中，存在明显的缺陷就是，发生哈希冲突后，会导致增删查的时间复杂度趋近O(n)。
在多线程环境下，基于数组实现的哈希表，只能给全局的表用互斥锁来保证原子操作，而链地址法，可以增加分段锁（每个桶都增加自己的互斥锁，那么对一个桶内的链表可以进行并发操作），保证了线程安全，并有一定的并发性。

链式哈希表解决哈希冲突的方法是链地址法，每个桶里维护一个链表，产生哈希冲突后，只需要增加一个节点，图示：

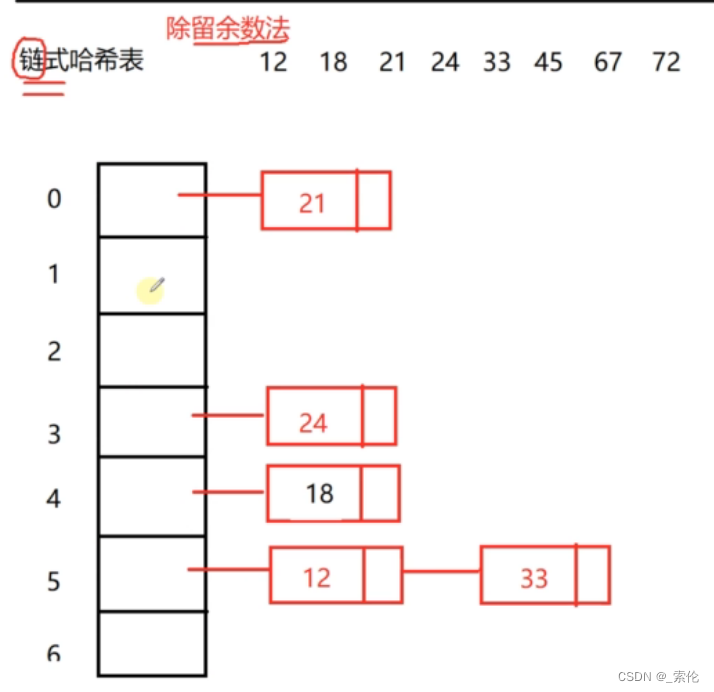
在这里插入图片描述

当然，如果一条链的节点太多，也会导致查询操作，接近O(n)，所以在有的版本的链式哈希表，每个桶维护的不是链表，而是红黑树，让查询时间为O(logn)。

哈希表的数据成员

直接使用STL的容器来表示哈希表

class HashTable
{
private:
	vector<list<int> > table_;			// 哈希表
	int useBucketNum_;					// 记录桶的个数
	double loadFactor_;					// 哈希表的装载因子

	static const int PRIME_SIZE = 10;	 // 素数表的大小
	static int primes_[PRIME_SIZE];		 // 素数表
	int primeIdx_;						 // 当前素数表的下标
};

int HashTable::primes_[HashTable::PRIME_SIZE] = { 3, 7, 23, 47, 97, 251, 443, 991, 1471, 42773 };

构造函数

依然是将哈希表大小调整为素数，申请空间交给STL来做。

HashTable(int size = primes_[0], double loadFactor = 0.75)
		: useBucketNum_(0)
		, loadFactor_(loadFactor)
		, primeIdx_(0)
{
	if (size != primes_[0])
	{
		for (; primeIdx_ < PRIME_SIZE; ++primeIdx_)
		{
			if (primes_[primeIdx_] >= size)
				break;
		}

		if (primeIdx_ == PRIME_SIZE)
		{
			primeIdx_--;
		}
	}
	table_.resize(primes_[primeIdx_]);
}

增加-insert()

判断是否要扩容
进行除留余数法，忘哈希表里插入，如果当前桶为nullptr，则需要把useBucketNum加一，再往当前链表里插入key。
如果不为nullptr，则需要进行去重，如果没有重复的，则插入key。

// 增加, 不能重复插入key
void insert(int key)
{
	// 判断扩容
	double factor = useBucketNum_ * 1.0 / table_.size();
	cout << "factor: " << factor << endl;

	if (factor > loadFactor_)
	{
		expand();
	}

	int idx = key % table_.size();
	if (table_[idx].empty())
	{
		useBucketNum_++;
		table_[idx].emplace_front(key);
	}
	else
	{
		// 使用泛型算法
		auto it = ::find(table_[idx].begin(), table_[idx].end(), key);
		if (it == table_[idx].end())
		{
			// key不存在
			table_[idx].emplace_front(key);
		}
	}
}

删除-erase()

除留余数法，找到待删除的位置。
使用泛型算法find()，若找到了该key，则删除节点，如果删除后链表为nullptr，则对useBucketNum减一。

// 删除
void erase(int key)
{
	int idx = key % table_.size();
	auto it = ::find(table_[idx].begin(), table_[idx].end(), key);
	if (it != table_[idx].end())
	{
		table_[idx].erase(it);
		// 如果删除后桶为null,则对使用个数减一
		if (table_[idx].empty())
		{
			useBucketNum_--;
		}
	}
}

查找-find()

// 搜索元素
bool find(int key) const
{
	int idx = key % table_.size();
	auto it = ::find(table_[idx].begin(), table_[idx].end(), key);
	
	return it != table_[idx].end();
}

扩容-expand()

素数表后移，得到扩容的大小。
申请一个哈希表对象，并与当前哈希表进行swap()操作（这个操作只是相当于把指针指向的地址交换，所以效率并不低，O(1)）。
根据素数表扩容当前，当作新的哈希表。
遍历旧的哈希表，把值重新哈希到新的哈希表中。

void expand()
{
	if (primeIdx_ + 1 == PRIME_SIZE)
		throw "HashTable can't expand anymore!";

	primeIdx_++;
	useBucketNum_ = 0;

	vector<list<int> > oldTable;
	// 交换两个容器成员变量
	table_.swap(oldTable);
	table_.resize(primes_[primeIdx_]);

	for (auto list : oldTable)
	{
		for (auto key : list)
		{
			int idx = key % table_.size();
			if (table_[idx].empty())
			{
				useBucketNum_++;
			}
			// key不存在
			table_[idx].emplace_front(key);
		}
	}
}

总结&扩展

优势：适用于快速的查找，时间复杂度O(1)。 100M整数哈希表 100M*2 = 200M 10亿个整数
4G * 2 = 8G

缺点：占用内存空间比较大。引用吴军博士的《数学之美》中所言，哈希表的空间效率还是不够高。如果用哈希表存储一亿个垃圾邮件地址，每个email地址对应 8bytes, 而哈希表的存储效率一般只有
50%，因此一个email地址需要占用16bytes. 因此一亿个email地址占用1.6GB，如果存储几十亿个
email address则需要上百GB的内存。除非是超级计算机，一般的服务器是无法存储的。 100M * 16
1600M 1.6G 空间换时间

散列函数：
设计特点：

计算简单（复杂会降低查找的时间）
散列地址分布均匀（减少哈希冲突）

散列函数(哈希函数)：

直接定址法：取关键字或关键字得某个线性函数值为散列地址。例如：f（key） = a * key + b（a、b为常数）
数字分析法：使用key的一部分来计算散列码（包括为了减少哈希冲突而进行位移操作、数字叠加操作等）
平方取中法：取关键字key的平方后的中间部分数字作为散列地址
折叠法&随机数法
除留余数法：f（key）= key mod p，不仅可以对关键字直接取模，也可以折叠、平方取中法等运算之后取模。 p的取值很重要，一般取素数，否则冲突的概率会比较大。
md5、sha加密hash算法等

散列冲突处理：

线性探测（开放定址法）
f（key）= （key + di）mod m （di = 1，2，3，4，…，m-1）
二次探测
f（key）= （key + di）mod m （di = 1^2，-12，2^2，-22，…，q^2，-q2） q<=m/2
二次探测是对线性探测法的改进，在散列冲突位置的前后都可以查找空位置，di取平方是为了让数据更加散列的存储，不会聚集。
链地址法：用链表存储组织产生哈希冲突的key