目录
1、冒泡排序
思想:每次左右两两比较,把最大或最小元素放到最后,直到整体有序
时间复杂度:O(n2)
稳定性:稳定
package com.xch2.DiGui;
import java.util.*;
public class Main7_1 {
//冒泡排序
//小到大排序
public static void f8(int[] arr) {
boolean flag=true;
int mid;
for (int i = arr.length-1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if(arr[j]>arr[j+1]) {
mid=arr[j];
arr[j]=arr[j+1];
arr[j+1]=mid;
flag=false;
}
}
//优化,提前整体有序
if(flag) {
return;
}
flag=true;
}
}
//大到小排序
public static void f9(int[] arr) {
boolean flag=true;
int mid;
for (int i = arr.length-1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if(arr[j]<arr[j+1]) {
mid=arr[j];
arr[j]=arr[j+1];
arr[j+1]=mid;
flag=false;
}
}
//优化,提前整体有序
if(flag) {
return;
}
flag=true;
}
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
int[] arr= {5,2,8,9,2,6,7,10};
// f8(arr);
f9(arr);
System.out.println(Arrays.toString(arr));
}
}
2、选择排序
思想:每次从待排数组中取一个最小或最大的元素放到前面,直到整体有序
时间复杂度:O(n2)
稳定性:不稳定
package com.xch2.DiGui;
import java.util.*;
public class Main7_1 {
//选择排序(简单选择排序)
//小到大排序
public static void f6(int[] arr) {
int min=arr[0],p=0,mid;
for (int i = 0; i < arr.length-1; i++) {
for (int j = i+1; j < arr.length; j++) {
if(arr[j]<min) {
p=j;
min=arr[j];
}
}
mid=arr[p];
arr[p]=arr[i];
arr[i]=mid;
min=arr[i+1];
p=i+1;
}
}
//大到小排序
public static void f7(int[] arr) {
int max=arr[0],p=0,mid;
for (int i = 0; i < arr.length-1; i++) {
for (int j = i+1; j < arr.length; j++) {
if(arr[j]>max) {
p=j;
max=arr[j];
}
}
mid=arr[p];
arr[p]=arr[i];
arr[i]=mid;
max=arr[i+1];
p=i+1;
}
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
int[] arr= {5,2,8,9,2,6,7,10};
// f6(arr);
f7(arr);
System.out.println(Arrays.toString(arr));
}
}
3、插入排序
思想:每次取一个元素拆入到已排序的数组中有序的位置,直到整体有序
时间复杂度:O(n2)
稳定性:稳定
package com.xch2.DiGui;
import java.util.*;
public class Main1 {
//插入排序
static void f8(int[] arr,int k) {//k代表个数或数组长度
if(k==1)//k代表元素个数
return;
f8(arr,k-1);//先把前k-1个元素排好序
int index=k-1;//index代表数组下标
while(index>0&&arr[index]<arr[index-1]) {
int mid=arr[index];
arr[index]=arr[index-1];
arr[index-1]=mid;
index--;
}
}
//方法二(前往后排序)
static void f9(int[] arr,int index) {//index代表开始下标,为0
if(index==arr.length)
return;
int r=index;
while(r>0&&arr[r]<arr[r-1]) {
int mid=arr[r];
arr[r]=arr[r-1];
arr[r-1]=mid;
r--;
}
f9(arr,index+1);//把剩余的index+1下标元素排序
}
//方法三(后往前排序)
static void f10(int[] arr,int index) {//index代表结束下标,为arr.length-1
if(index==-1)
return;
int r=index;
while(r<arr.length-1&&arr[r]>arr[r+1]) {
int mid=arr[r];
arr[r]=arr[r+1];
arr[r+1]=mid;
r++;
}
f10(arr,index-1);//把剩余的index-1下标元素排序
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
int[] arr1=new int[]{2,5,99,5,1,-5,-9};
f8(arr1,7);
for (int i = 0; i < arr1.length; i++) {
System.out.print(arr1[i]+",");
}
System.out.println();
int[] arr2=new int[]{2,5,99,5,1,-5,-9};
f9(arr2,0);
for (int i = 0; i < arr2.length; i++) {
System.out.print(arr2[i]+",");
}
System.out.println();
int[] arr3=new int[]{2,5,99,5,1,-5,-9};
f10(arr3,6);
for (int i = 0; i < arr3.length; i++) {
System.out.print(arr3[i]+",");
}
System.out.println();
}
}
4、希尔排序
思想:确定一个渐进缩小的增量,进行分组后在组内插入排序,直到整体有序(插入排序的进阶版)
时间复杂度:O(nlogn)
稳定性:不稳定
package com.xch2.DiGui;
import java.util.*;
public class Main2 {
//希尔排序(缩小增量排序,优化插入排序)
static void f2(int arr[]) {
for (int incre = arr.length/2; incre > 0; incre=incre/2) {
for (int i = incre; i < arr.length; i++) {
int target=i;
while(target>=incre&&arr[target]<arr[target-incre]) {
int mid=arr[target];
arr[target]=arr[target-incre];
arr[target-incre]=mid;
target-=incre;
}
}
}
}
public static void main(String[] args) {
// TODO 自动生成的方法存根=
int arr1[]=new int[] {9,8,7,6,5,4,3,6,2,1,99,0,-4};
f2(arr1);
for (int i : arr1) {
System.out.print(i+",");
}
System.out.println();
}
}
5、归并排序
思想:分治思想,把待排数组渐进分割,进行有序合并,直到整体有序(偏合并)
时间复杂度:O(nlogn)
稳定性:稳定
package com.xch2.DiGui;
public class Main5 {
//归并排序
static int[] arr1;
static void f1(int[] arr,int l,int r) {
arr1=new int[arr.length];//外移到递归函数外,不会多次new节省存储空间
f2(arr,l,r);
}
static void f2(int[]arr,int l,int r) {
if(l>=r)//递归出口
return;
int mid=l+((r-l)>>1),left=l,right=mid+1,ori=l;
f2(arr,l,mid);//子递归
f2(arr,mid+1,r);
for (int i = 0; i < arr1.length; i++) {
arr1[i]=arr[i];//更新辅助数组
}
while(left<=mid&&right<=r) {//递归体
if(arr1[left]<=arr1[right]) {
arr[ori]=arr1[left];
left++;
}else {
arr[ori]=arr1[right];
right++;
}
ori++;
}
while(left<=mid) {
arr[ori]=arr1[left];
left++;
ori++;
}
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
int[] arr=new int[] {11,8,3,4,9,8,22,0,5,8,3};
f1(arr,0,10);
for (int i : arr) {
System.out.print(i+" ");
}
System.out.println();
}
}
6、快速排序
思想:分治思想,先定主元把数组分为两(三)段[小于(等于)大于],后调整主元位置,递归渐进分割比较,直到整体有序(偏拆分)
时间复杂度:O(nlogn)
稳定性:不稳定
其中,实现方法分为三种:
1、双指针-单向扫描快速排序
2、双指针-双向扫描快速排序
3、三指针-双向扫描快速排序(相等元素优化)
定主元的两种方法:
1、取第一个
2、三点中值法(推荐,取本段数组头中尾三个元素比较值)
package com.xch2.DiGui;
public class Main4 {
//单向单指针扫描分区快排法
static void f1(int[] arr,int l,int r) {
if(l>=r)//递归出口
return;
int left=l+1,right=r,mid=0;
while(left<=right) {//递归体
if(arr[left]<=arr[l])
left++;
else {
mid=arr[left];
arr[left]=arr[right];
arr[right]=mid;
right--;
}
}
mid=arr[right];
arr[right]=arr[l];
arr[l]=mid;
f1(arr,l,right-1);//子递归
f1(arr,right+1,r);
}
//双向双指针扫描分区快排法
static void f2(int[] arr,int l,int r) {
if(l>=r)//递归出口
return;
int left=l+1,right=r,mid=0;
while(left<=right) {//递归体
while(left<=right&&arr[left]<=arr[l])
left++;
while(left<=right&&arr[right]>arr[l])
right--;
if(left<right) {
mid=arr[right];
arr[right]=arr[left];
arr[left]=mid;
}
}
mid=arr[right];
arr[right]=arr[l];
arr[l]=mid;
f2(arr,l,right-1);//子递归
f2(arr,right+1,r);
}
//双向和等于三指针扫描分区快排法
static void f3(int[] arr,int l,int r) {
if(l>=r)//递归出口
return;
int equ=l,left=l+1,right=r,mid=0;
while(left<=right) {//递归体
while(left<=right&&arr[left]<=arr[l]) {
if(arr[left]==arr[l]&&equ==l)
equ=left;
if(arr[left]<arr[l]&&equ!=l) {
mid=arr[left];
arr[left]=arr[equ];
arr[equ]=mid;
equ++;
}
left++;
}
while(left<=right&&arr[right]>arr[l])
right--;
if(left<right) {
mid=arr[right];
arr[right]=arr[left];
arr[left]=mid;
}
}
if(equ!=l) {
equ--;
mid=arr[equ];
arr[equ]=arr[l];
arr[l]=mid;
f3(arr,l,equ-1);//子递归
f3(arr,right+1,r);
}else {
mid=arr[right];
arr[right]=arr[l];
arr[l]=mid;
f3(arr,l,right-1);//子递归
f3(arr,right+1,r);
}
}
//以上方法均为去第一个随机数为比较主元
//一般用三点取中值法取比较主元,如f4单指针,其他一样(取中值后和第一个数值换成为主元)
//单向单指针扫描分区快排法(三点取中值为主元法)
static void f4(int[] arr,int l,int r) {
if(l>=r)//递归出口
return;
int left=l+1,right=r,mid=0;
int midsub=l+((r-l)>>1);//三点取中值
if(arr[l]>=arr[midsub]&&arr[midsub]>=arr[r]||
arr[l]<=arr[midsub]&&arr[midsub]<=arr[r]) {
mid=arr[midsub];
arr[midsub]=arr[l];//换主元
arr[l]=mid;
}else if(arr[midsub]>=arr[r]&&arr[r]>=arr[l]||
arr[midsub]<=arr[r]&&arr[r]<=arr[l]){
mid=arr[r];
arr[r]=arr[l];
arr[l]=mid;
}
while(left<=right) {//递归体
if(arr[left]<=arr[l])
left++;
else {
mid=arr[left];
arr[left]=arr[right];
arr[right]=mid;
right--;
}
}
mid=arr[right];
arr[right]=arr[l];
arr[l]=mid;
f4(arr,l,right-1);//子递归
f4(arr,right+1,r);
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
int[] arr=new int[] {0,1,9,5,4,1};
// f1(arr,0,5);
// f2(arr,0,5);
// f3(arr,0,5);
f4(arr,0,5);
for (int i : arr) {
System.out.print(i+" ");
}
System.out.println();
}
}
7、堆排序
思想:利用二叉树的特性,每次把最大或最小的元素比较到根节点维持一个大或小顶堆,取出根节点放到最后,直到整体有序
时间复杂度:O(nlogn)
稳定性:不稳定
分为两种:
1、小顶堆-逆向排序
2、大顶堆-顺向排序
package com.xch2.DiGui;
import java.util.*;
public class Main7 {
//堆排序(小顶堆=逆序,大顶堆=顺序)
//建小顶堆
static void f1(int[] arr,int index,int leng) {//index初始为数组二分值减一
if(index<0) //leng 初始为数组长度
return;
int left=2*index+1,right=2*index+2,mid;
if(left==leng-1) {//最后一个父节点为单亲节点
if(arr[left]<arr[index]) {
mid=arr[left];
arr[left]=arr[index];
arr[index]=mid;
}
}else {
if(arr[left]<=arr[right]&&arr[left]<arr[index]) {
mid=arr[left];
arr[left]=arr[index];
arr[index]=mid;
}else if(arr[right]<=arr[left]&&arr[right]<arr[index]) {
mid=arr[right];
arr[right]=arr[index];
arr[index]=mid;
}
}
f1(arr,index-1,leng);
}
//小顶堆转逆序数组
static void f2(int arr[],int leng) {
if(leng==1)
return;
f1(arr,leng/2-1,leng);
int mid=arr[leng-1];
arr[leng-1]=arr[0];
arr[0]=mid;
leng--;
f2(arr,leng);
}
//建大顶堆
static void f3(int[] arr,int index,int leng) {//index初始为数组二分值减一
if(index<0) //leng 初始为数组长度
return;
int left=2*index+1,right=2*index+2,mid;
if(left==leng-1) {//最后一个父节点为单亲节点
if(arr[left]>arr[index]) {
mid=arr[left];
arr[left]=arr[index];
arr[index]=mid;
}
}else {
if(arr[left]>=arr[right]&&arr[left]>arr[index]) {
mid=arr[left];
arr[left]=arr[index];
arr[index]=mid;
}else if(arr[right]>=arr[left]&&arr[right]>arr[index]) {
mid=arr[right];
arr[right]=arr[index];
arr[index]=mid;
}
}
f3(arr,index-1,leng);
}
//大顶堆转顺序数组
static void f4(int arr[],int leng) {
if(leng==1)
return;
f3(arr,leng/2-1,leng);
int mid=arr[leng-1];
arr[leng-1]=arr[0];
arr[0]=mid;
leng--;
f4(arr,leng);
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
int arr[]= {5,2,8,9,2,6,7,10};
// f1(arr,arr.length/2-1,8);
f2(arr,8);
// f3(arr,arr.length/2-1,8);
// f4(arr,8);
for (int i : arr) {
System.out.print(i+" ");
}
System.out.println();
}
}
8、计数排序
思想:利用数组的特性,把元素值记录到新的辅助数组对应下标中,后顺序恢复即可(适用于元素较为集中的排序,如年龄、分数等)
时间复杂度:O(n)
稳定性:稳定
package com.xch2.DiGui;
import java.util.*;
public class Main7 {
//计数顺序排序(包含负数)
static void f5(int[] arr) {
int cur=0,max=0,min=0;
for (int i : arr) {
if(i>max)
max=i;
else if(i<-min)
min=-i;
}
int[] helper=new int[max+1];
int[] helper1=new int[min+1];
for (int i : arr) {
if(i>=0)
helper[i]++;
else
helper1[-i]++;
}
for (int i = helper1.length-1; i > 0; i--) {
while(helper1[i]>0) {
arr[cur]=-i;
helper1[i]--;
cur++;
}
}
for (int i = 0; i < helper.length; i++) {
while(helper[i]>0) {
arr[cur]=i;
helper[i]--;
cur++;
}
}
}
//方法二
static void f5_1(int[] arr){
int max=0,min=0,cur=0;
for (int i : arr) {
if(i>max)
max=i;
else if(i<min)
min=i;
}
for (int i = 0; i < arr.length; i++) {
arr[i]-=min;//把所有负数转正数
}
int[] helper=new int[max-min+1];
for (int i : arr) {
helper[i]++;
}
for (int i = 0; i < helper.length; i++) {
while(helper[i]!=0) {
arr[cur]=i+min;//恢复原数组输出
helper[i]--;
cur++;
}
}
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
// int arr1[]= {-3,2,4,-3,66,4,66,9,0,-90,2};
// // f5(arr1);
// f5_1(arr1);
// System.out.println(Arrays.toString(arr1));
}
}
9、桶排序
思想:利用链表的特性,通过公式把数组分为多个数段的子链表(桶,元素进入链表时是有序插入),再顺序取出即可(计数排序的进阶版:浪费率相比更低、适用数据分布相比更广)
时间复杂度:O(n)
稳定性:稳定
package com.xch2.DiGui;
import java.util.*;
public class Main7 {
//桶排序(包含负数)
static void f6(int[] arr) {
int max=arr[0],min=arr[0],cur=0;
for (int i : arr) {
if(i>max)
max=i;
else if(i<min)
min=i;
}
List<LinkedList<Integer>> bucketlist=new ArrayList<>();
for (int i=0;i<arr.length;i++) {
bucketlist.add(new LinkedList<Integer>());//初始化桶
}
for (int i : arr) {
int num=(i-min)*arr.length/(max-min+1);//最优公式,元素放置桶
bucketlist.get(num).add(i);
}
for (LinkedList<Integer> linkedlist:bucketlist) {
Collections.sort(linkedlist);//归并排序桶中的集合
}
for (LinkedList<Integer> linkedlist:bucketlist) {
for (Integer integer : linkedlist) {
arr[cur]=integer;//遍历输出
cur++;
}
}
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
// int arr1[]= {-3,2,4,-3,66,4,66,9,0,-90,2};
// // f6(arr1);
// System.out.println(Arrays.toString(arr1));
}
}
10、基数排序
思想:利用链表的特性,通过数字的位数(个-十-百…)渐进顺序分配到链表中,再顺序收集即可,直到最高位即整体有序(桶排序的进阶版)
时间复杂度:O(n)
稳定性:稳定
package com.xch2.DiGui;
import java.util.*;
public class Main7 {
//基数排序(包含负数)
static void f7(int[] arr) {
List<Integer>[] bucketarr=new List[10];
for (int i = 0; i < bucketarr.length; i++) {
bucketarr[i]=new LinkedList<Integer>();//初始化数组中的集合
}
int maxd=0,min=arr[0];
for (int i:arr) {
int len=(i+"").length();
if(len>maxd)
maxd=len;//找最大位数
if(i<min)
min=i;//找最小值
}
if(min<0) {
for (int i = 0; i < arr.length; i++) {
arr[i]=arr[i]-min;//负数移位转正数
}
}
int der=1,cur=0;
for (int i = 1; i <= maxd; i++) {
for (int j = 0; j < arr.length; j++) {
int x=(arr[j]/der)%10;
bucketarr[x].add(arr[j]);//入桶
}
for (int j = 0; j < bucketarr.length; j++) {
for (Integer value : bucketarr[j]) {
arr[cur]=value;//出桶
cur++;
}
bucketarr[j].clear();
}
der*=10;
cur=0;
}
if(min<0) {
for (int i = 0; i < arr.length; i++) {
arr[i]=arr[i]+min;//负数移位复原
}
}
}
public static void main(String[] args) {
// TODO 自动生成的方法存根
// int arr1[]= {-3,2,4,-3,66,4,66,9,0,-90,2};
// // f7(arr1);
// System.out.println(Arrays.toString(arr1));
}
}
十大排序算法的时间复杂度:
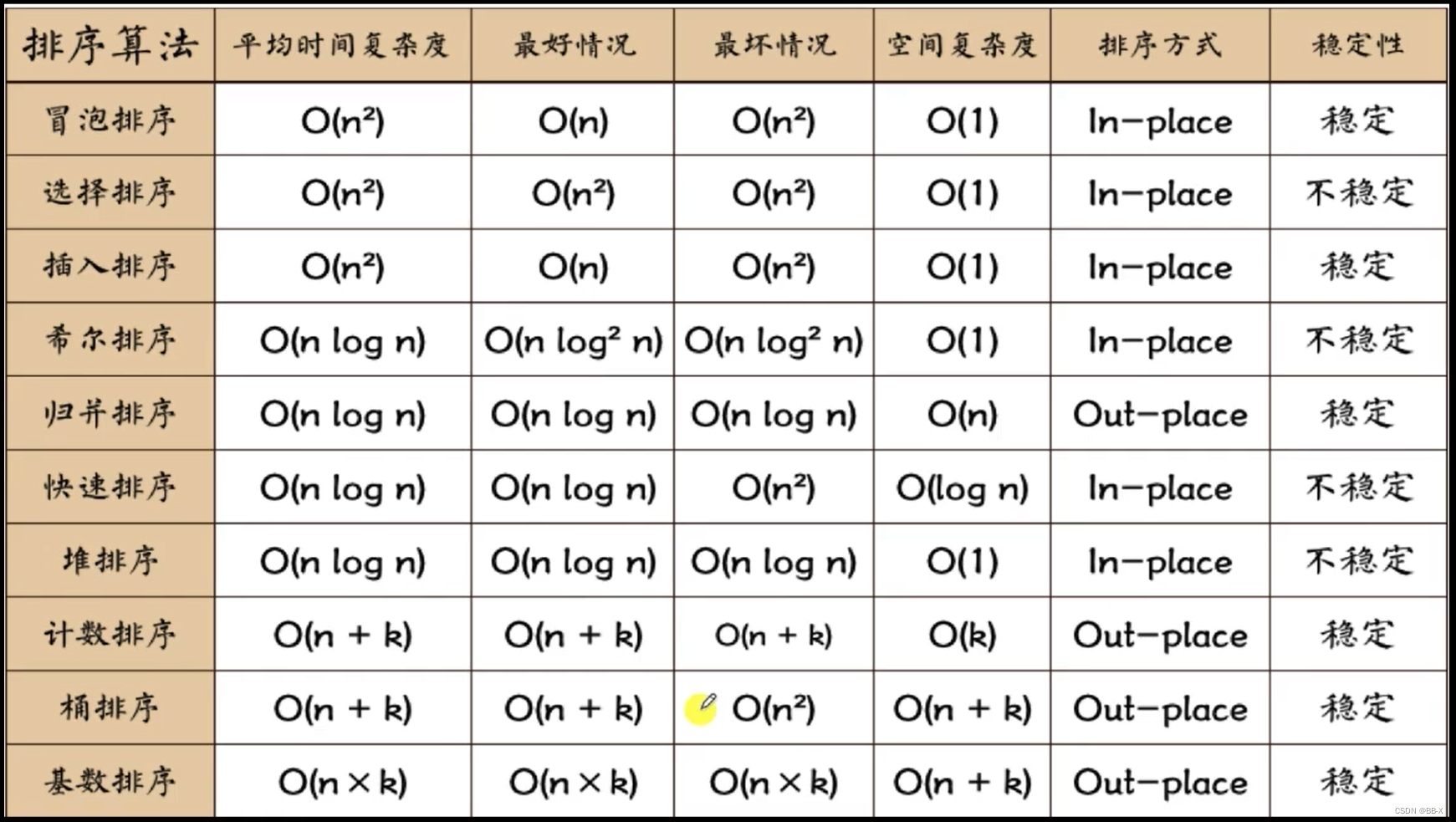
时间复杂度效率对比:?
