见山是山,见水是水,见你即是全世界

大家好,这里是新一,请多关照🙈🙉🙊。在本篇博客中,新一将会为大家介绍数据结构与算法之队列篇,为了方便大家理解,新一特地给大家附上了 源码和图片
便于大家理解,干货满满哟。(以下结果均在IDEA中编译)希望在方便自己复习的同时也能帮助到大家。😜😜😜🥇🥈🥉
废话不多说,直接进入我们的文章。
文章目录
一.🌕 队列基本认知
1.1🍂 队列的概念
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有 先进先出 的性质
入队: 队尾插入操作
出队: 队头删除操作
我们的队列是从队尾先进入,然后从队头出来,因此是先进先出

1.2🍂 队列的结构
我们知道顺序表和链表是整个线性表的基础结构,那么我们的队列用哪个来实现呢?我们先来对比一下顺序表跟链表
1.2.1 🍃顺序表与链表的对比
顺序表优点:
- 顺序表的 内存空间连续
- 支持 随机访问,可以高效的按下标进行操作,时间复杂度是O(1)。
顺序表缺点:
- 顺序表插入删除操作 需要挪动元素,效率较低(O(n))
- 顺序表空间 大小固定,必要时需要扩容
链表优点:
- 链表 按需求申请空间,不存在扩容问题
- 链表任意位置 插入删除 时间复杂度为O(1),可以支持高频的插入删除操作
链表缺点:
链表 不支持下标的随机访问
经过以上对比,我们发现,既然我们要实现队列,肯定就要 频繁的涉及到队列的入出队操作, 我们分别再来看几组图示,我们定义 队头为front,队尾为rear, 再来分别看看顺序表跟链表于队列的实现.。
1.2.2 🍃顺序表实现队列
顺序表的底层实际上就是个数组,我们就用数组来表示,当入队时,队尾指针后移,出队时,队头指针后移, 我们这里以20-70为例子。
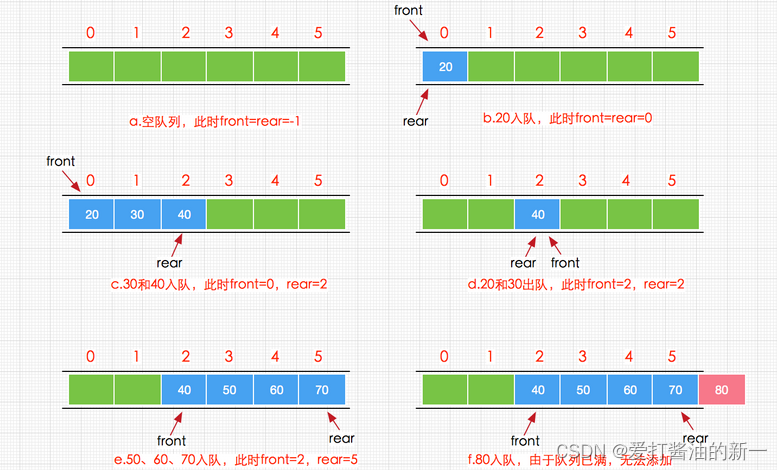
我们看到当进行到我们的最后一步,队尾指针已经到达我们数组下标的最大值,但是此时我们的队列满了吗?到达最大值不就是满了吗?真的满了么?😨,我们发现如果在这中间的任何一步出队了,那么数组前面的下标所指元素为空,也就是说,满了,但没完全满, 那么此时我们便可以看出使用数组实现队列实在不是很妥当,那么如果我们非要真正意义上的放满呢?😲,有没有一种可能我们可以使用一种魔法,让rear从最后一个元素直接瞬移回第一个,然后又继续放——咳咳这个我们放到后文来说🤞
1.2.3 🍃链表实现队列
对比上述顺序表,我们利用链表来实现队列的入队出队岂不是手到擒来,而且还不用考虑其空间满的问题,实属是完美融合😲,但是我们普通的单链表可以吗?真的可以吗?😵,我们队列的 入队操作是要在队尾,对应着链表的尾插, 而 出队操作是要在队头,对应着链表的头删, 出队操作倒是很简单,头结点(front)后移即可,那么入队呢?遍历?那不就成跟顺序表差不多啦?其实我们只需要加个尾指针(rear),入队是找到尾指针,尾指针指向新节点即可。
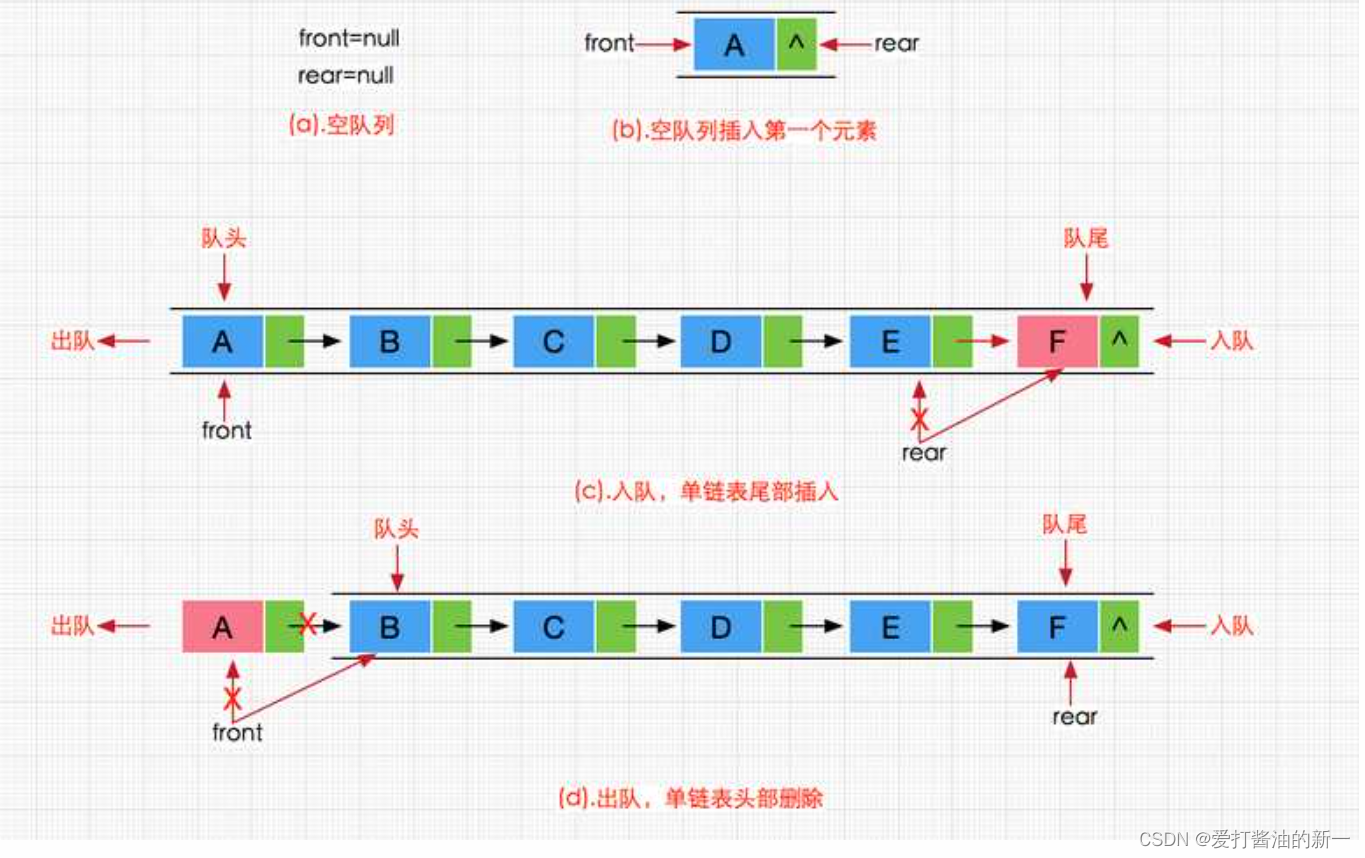
二.🌕 队列的基本实现
我们对比了这两种情况,发现还是链表比较好实现,那么我们先来肝链表实现队列
2.1🍂 链表型队列
为了方便大家理解,新一这里用图片注释 + 源码的方式给大家呈现。
2.1.1 🍃节点信息
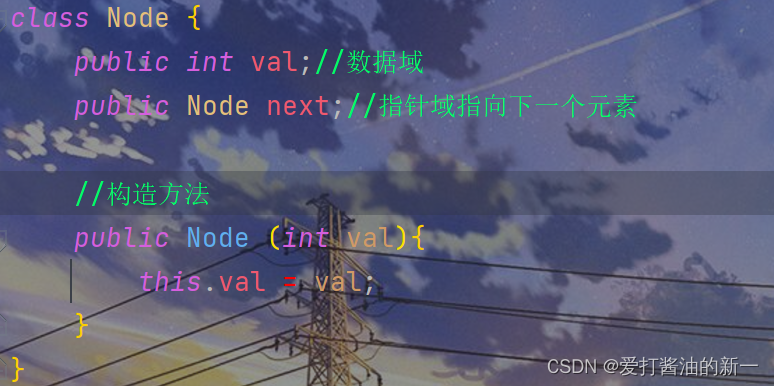
class Node {
public int val;
public Node next;
public Node (int val){
this.val = val;
}
}
2.1.2 🍃入队操作

public Node head;//头结点 - 出队
public Node last;//尾结点 - 入队
/**
* 入队
* @param val 数据
*/
public void offer(int val){
Node node = new Node(val);//生成新节点
if (head == null){//判断当前是否为空队列
head = node;
last = node;
}else{//不为空,正常尾指针后移
last.next = node;
last = node;
}
}
2.1.3 🍃判空操作

public boolean isEmpty(){
return this.head == null;//直接返回表达式的布尔值即可
}
2.1.4 🍃出队操作
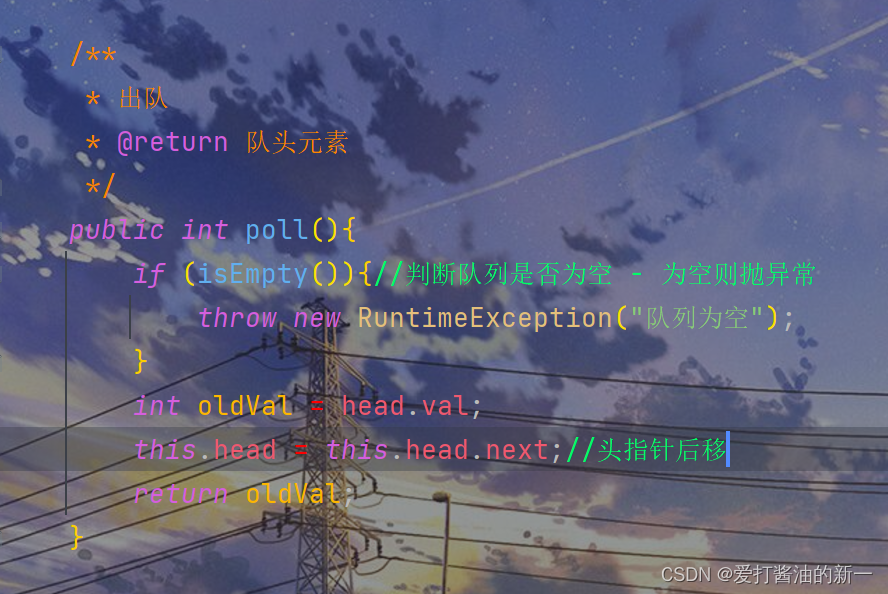
/**
* 出队
* @return 队头元素
*/
public int poll(){
if (isEmpty()){//判断队列是否为空 - 为空则抛异常
throw new RuntimeException("队列为空");
}
int oldVal = head.val;
this.head = this.head.next;//头指针后移
return oldVal;
}
2.1.5 🍃获取队头

public int peek(){
if(isEmpty()){//判空
throw new RuntimeException("队列为空");
}
return head.val;//返回头结点值
}
2.2🍂 数组型循环队列
我们前面说的后文它来了,那么到底有没有一种魔法能使本在最后的rear下标直接循环为0下标从而继续放元素呢?——当然有,那就是 循环队列
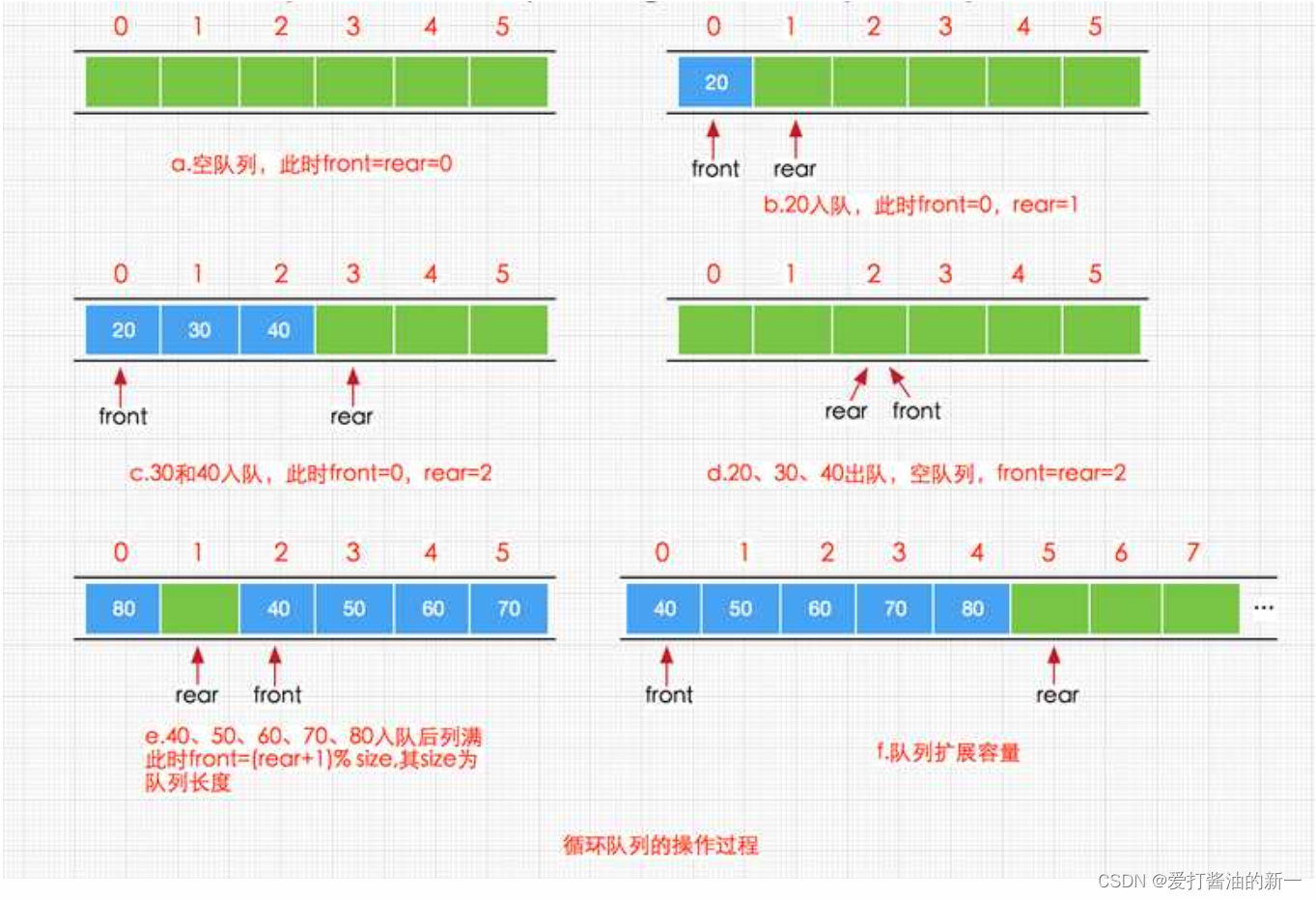
什么?看不懂?太抽象了,那下面这个呢
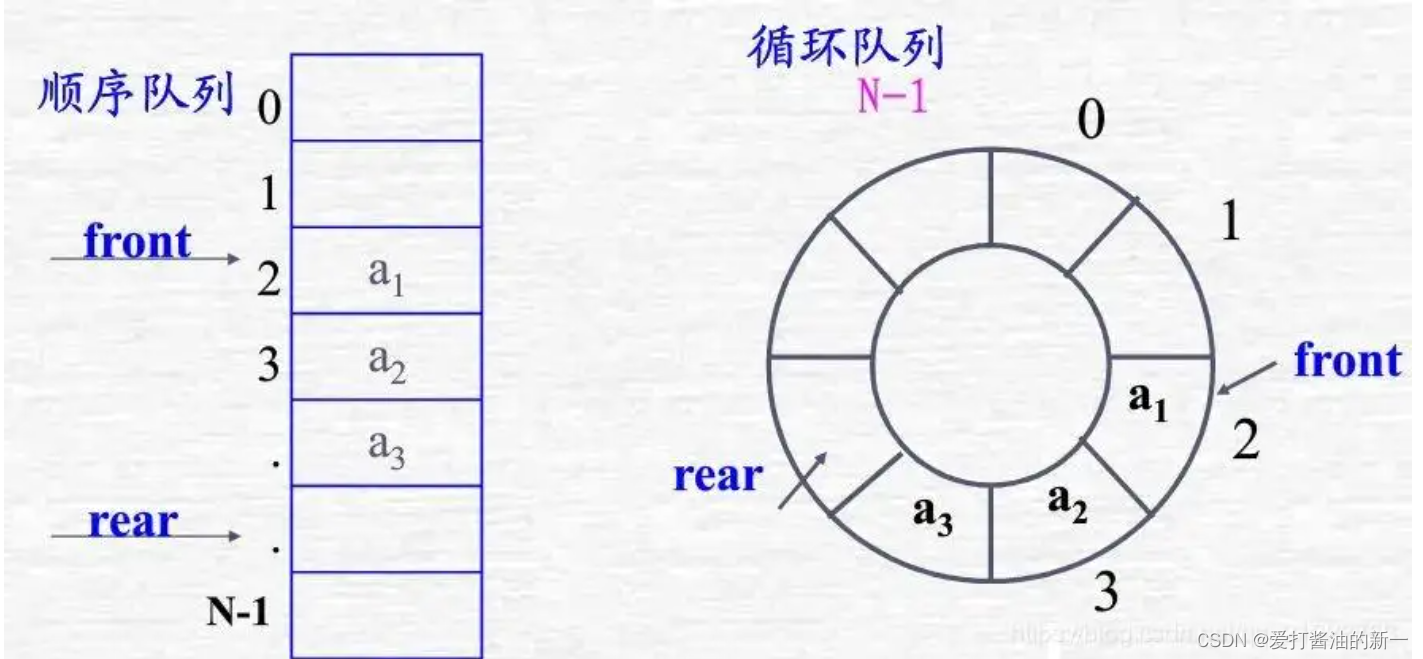
当我们的rear或者front指针到达数组下标最大值,我们用两个公式既可以移动又可以达到循环的效果
rear指针移动时:rear = (rear + 1) % elem.length
front指针移动时:front = (front + 1) % elem.length
但是同时这样也出现了一个问题:什么时候满?什么时候空? 😵
我们很容易想到的是既然入队rear++,出队front++,那么空的时候不就是初始状态rear == front, 那么满呢?也是rear == front?——这样不就条件重复了吗,肯定不行,既然如此,那么我们不妨就牺牲一个空间,当rear + 1 = front 时即满。 好,那么问题又来了,当rear等于最大下标时,我们还能rear + 1吗?当然不能,相信此时已经有很多小伙伴想到了,运用公式:(rear + 1) % elem.length == front 判满即可。
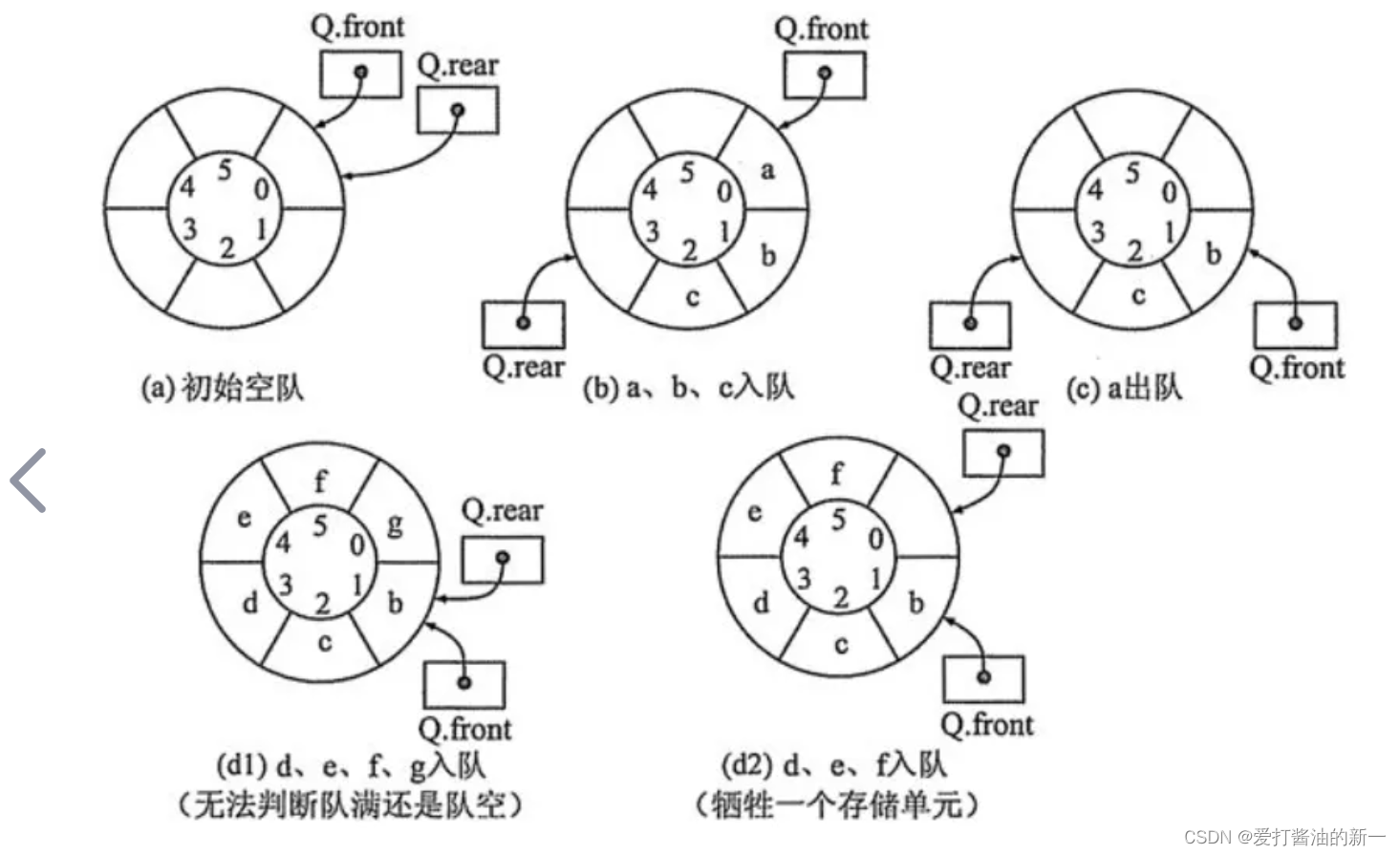
好了,现在开始来设计我们的循环队列:
2.2.1 🍃节点信息
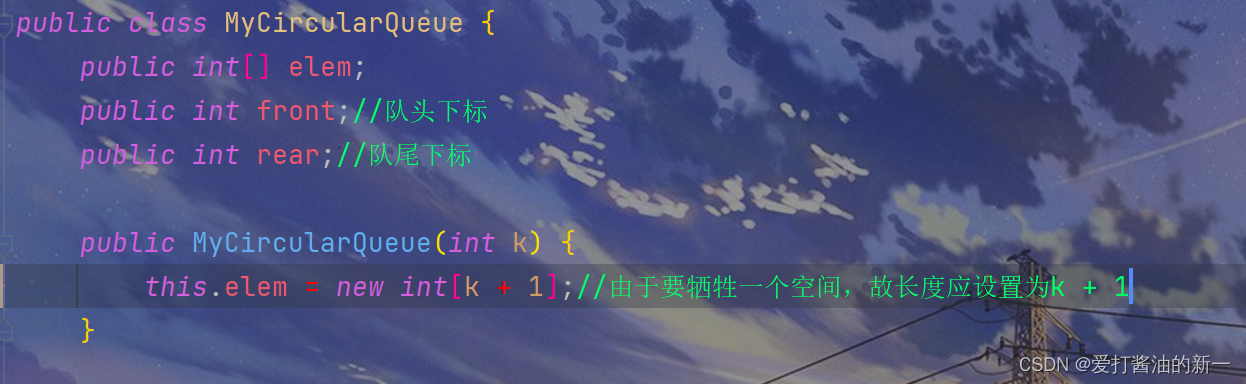
public int[] elem;
public int front;//队头下标
public int rear;//队尾下标
public MyCircularQueue(int k) {
this.elem = new int[k + 1];//由于要牺牲一个空间,故长度应设置为k + 1
}
2.2.2 🍃判空操作
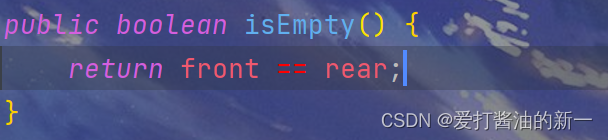
public boolean isEmpty() {
return front == rear;
}
2.2.3 🍃判满操作

public boolean isFull() {
//直接返回其布尔值即可
return (this.rear + 1) % elem.length == front;
}
2.2.4 🍃入队操作
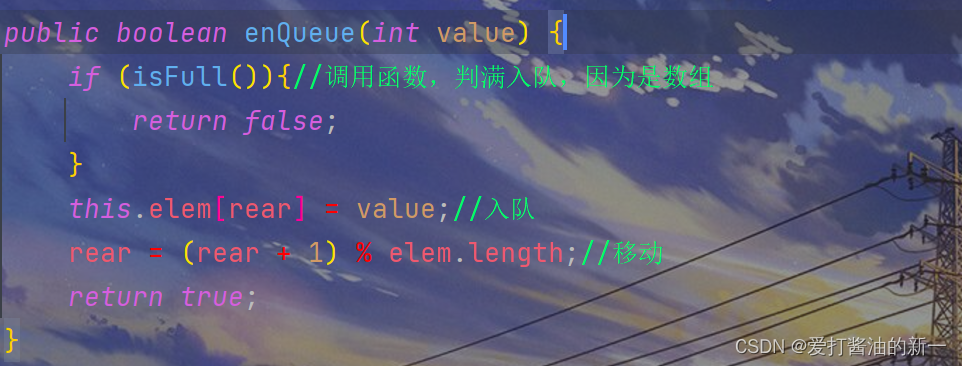
public boolean enQueue(int value) {
if (isFull()){//调用函数,判满入队,因为是数组
return false;
}
this.elem[rear] = value;//入队
rear = (rear + 1) % elem.length;//移动
return true;
}
2.2.5 🍃出队操作

public boolean deQueue() {
if (isEmpty()){//调用函数,判空出队
return false;
}
front = (front + 1) % elem.length;//只需移动即可,后续元素会被自然入队覆盖掉
return true;
}
2.2.6 🍃获取队头
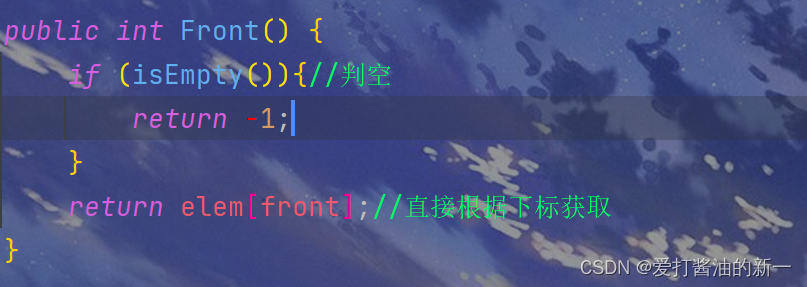
public int Front() {
if (isEmpty()){//判空
return -1;
}
return elem[front];//直接根据下标获取
}
2.2.7 🍃获取队尾
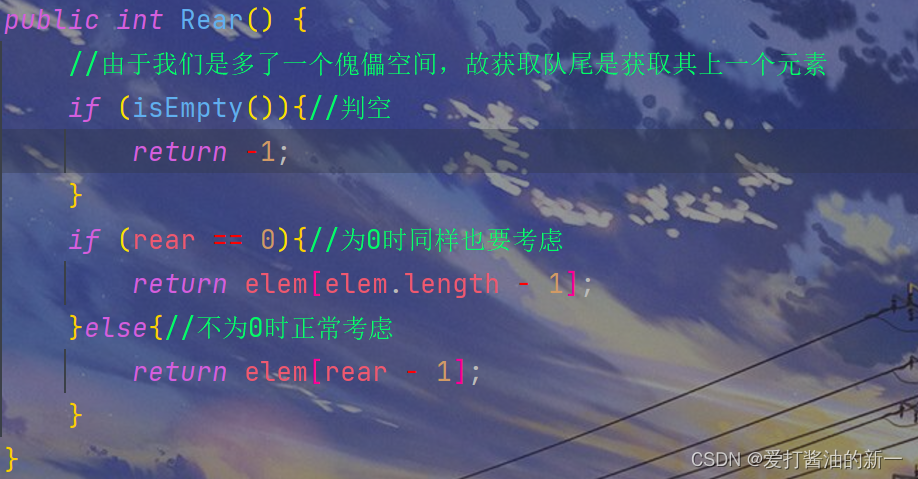
public int Rear() {
//由于我们是多了一个傀儡空间,故获取队尾是获取其上一个元素
if (isEmpty()){//判空
return -1;
}
if (rear == 0){//为0时同样也要考虑
return elem[elem.length - 1];
}else{//不为0时正常考虑
return elem[rear - 1];
}
}
2.3🍂 双端队列
Deque(双端队列)这是一个很特殊的队列,它底层是一个双向链表,因此它支持 头插,尾插,头删,尾删,

我们可以在IDEA中看看它的方法到底有哪些:
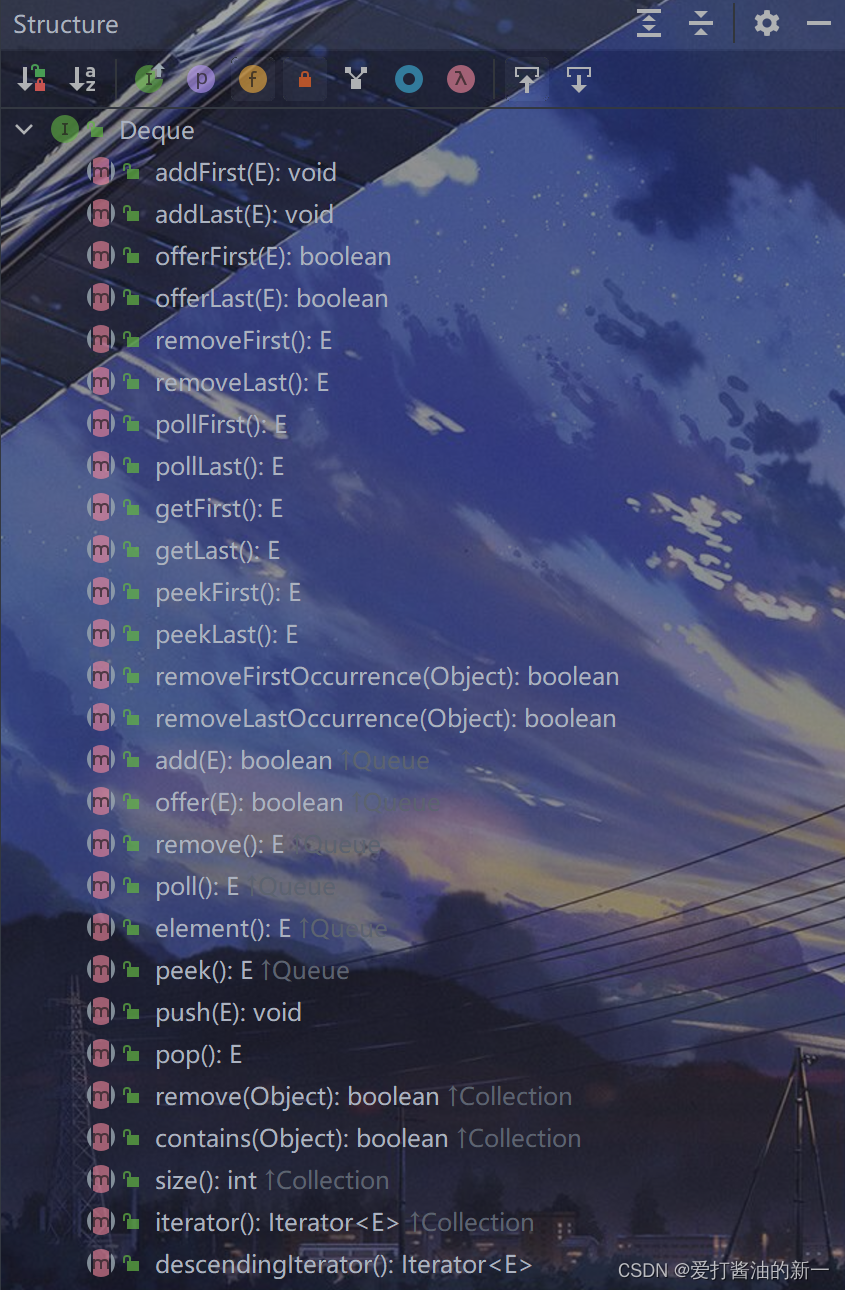
整整一页啊,家人们,而且不知道大家发现没,里边许多方法的功能都是重复的
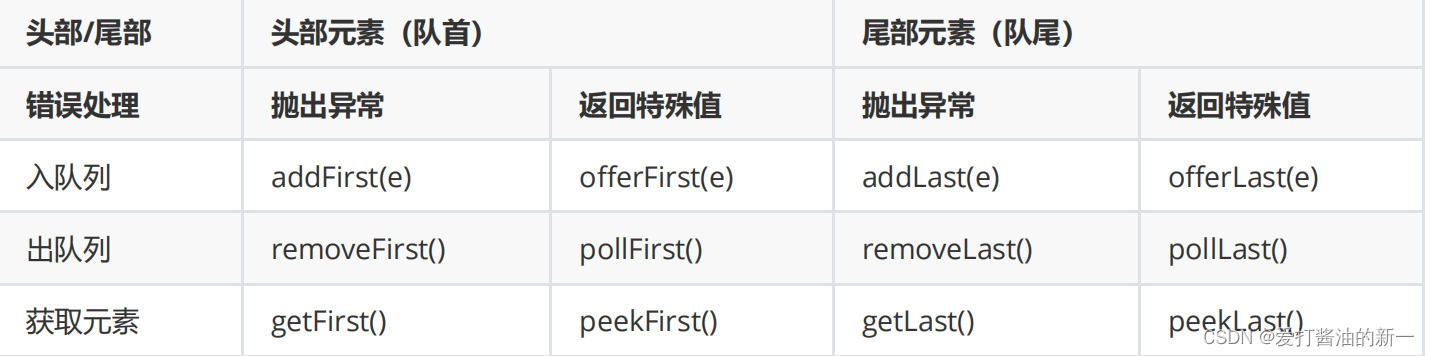
正因为这样的双端队列这样的特殊性,我们可以把它当做栈来使用,也可以将它当做队列来使用,还可以将它当做链表来使用,感觉是不是很方便,嘿嘿💕
想对大家说的话
💕家人们,学到这里我们的数据结构与算法中的队列已经彻底弄懂啦,但这只是数据结构中很基础的一部分,后续新一还会对数据结构进行很多的补充,如果觉得新一讲得还清楚的话,可以点个赞支持一下哦🥳🥳🥳,后续新一会持续更新JAVA的有关内容,学习永无止境,技术宅,拯救世界!
