一、算法原理
归并排序是一种常用的排序算法,属于稳定排序法。
归并排序就是将两个已经分别排好序的数组A和B合并为一个排好序的数组C。
如果数组散乱的数组,则需要将数组元素分别按照长度为d=2^n,n=0,1,2,3,…,进行分组,然后对相邻的两组进行归并排序。具体过程就是首先取长度d=1,即将数组的每个元素作为一个子数组,然后把相邻的两个子数组作为一对进行归并排序,直到整个数组均排序完成。之后进行长度d=2,即把相邻的两个元素作为一个子数组,再对两个相邻的子数组进行归并排序,直到整个数组排序完成。之后再分别进行d=4,8,…的归并排序,直到整个数组已经是排好序的数组结束。
本文给出了归并排序算法的另外一种实现方法,不同于作者在https://blog.csdn.net/sunnyoldman001/article/details/127008922给出的实现方法。
以下Demo演示归并排序的过程。
**Demo:**假设有数据如下表所示:

第一趟归并排序: 每个元素为一个数组,总共有7个,相邻的两个数组依次进行排序,过程如下:
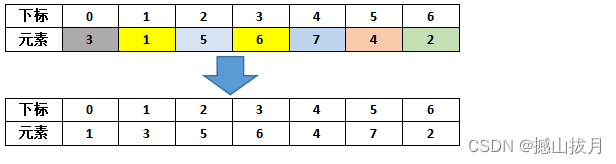
第二趟归并排序: 相邻的2个元素组成一个数组,不足的部分也自成一个数组,总共有4个,相邻的两个数组依次进行排序,过程如下:
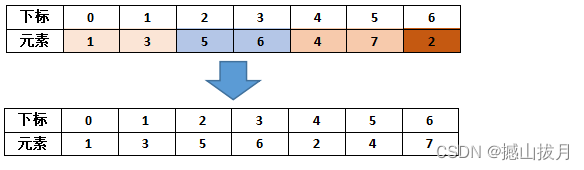
第三趟归并排序: 相邻的4个元素组成一个数组,不足的部分也自成一个数组,总共有2个,相邻的两个数组依次进行排序,过程如下:
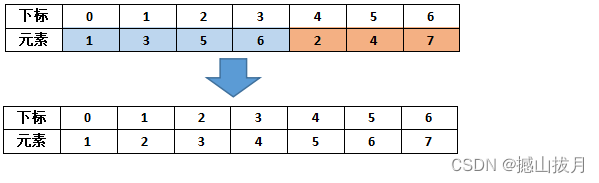
至此,归并排序结束。
由上述归并排序过程可以看出,数组中的元素在每一趟归并排序中,不一定能刚好分成偶数个数组,可能会存在“尾巴”数据。在编制算法的时候,就需要单独考虑这些“尾巴”的排序问题。当剩余的“尾巴”元素个数小于等于d的长度时,对这些数据不需要处理,如上述Demo的第一趟归并排序,剩余尾巴元素2。当剩余的“尾巴”元素个数大于d的长度小于2d长度时,需要分成2组进行归并排序,如上述Demo的第二趟排序中,剩余的尾巴元素4,7和2,则4,7组成一个数组,2组成一个数组,然后进行归并排序。
从上述Demo可以看出,归并排序的原理非常简单。只是在处理“尾巴”元素时,需要单独考虑而已。
二、归并排序算法之C程序
在https://blog.csdn.net/sunnyoldman001/article/details/127008922中给出了归并排序算法实现的方法一,该方法是把每次归并排序中用到的两个子数组单独拿出来进行排序,然后再还回到原数组中。由于不同趟归并排序中子数组的长度不同,因此每一轮次都需要重新分配子数组的大小,虽然算法对于初学者来说比较容易理解,但是这样也导致了算法实现起来比较麻烦,代码行数比较多。
本文中给出的方法二,只是多使用了一个和原数组长度相同的数组来缓存每趟排序的结果,在每一次归并排序时,从原数组直接截取子数组进行归并排序,排序后缓存到新数组的相应位置上,这样就省去了每一趟都分配子空间的麻烦。
1.两个子数组的归并排序
//对数组a从下标start到start+m-1的元素与从start+m到start+m+n-1归并排序并存储到数组b从start到start+m+n-1位置
void Merge( int a[], int b[], int m, int n, int start )
{
int i, j, k;
i = start;
j = start + m;
k = start;
while( i < start + m && j < start + m + n )
{
if( a[i] < a[j] )
{
b[k++] = a[i++];
}
else
{
b[k++] = a[j++];
}
}
while( i < start + m )
{
b[k++] = a[i++];
}
while( j < start + m + n )
{
b[k++] = a[j++];
}
}
2.对数组进行归并排序
//对长度为len的数组arr使用归并排序算法进行排序
//该方法使用了和arr相同长度的静态数组作为缓存
void MergeSort( int arr[], int len )
{
int k, n, m, x, xx;
unsigned int d;
x = int ( log(len) / log(2) );
//printf( "指数x=%d\n", x );
int *b = new int[len];//缓存
//处理排序的趟数
if( int( pow( 2, x ) ) == len )
{
xx = x - 1;
}
else
{
xx = x;
}
//根据事先计算的趟数进行归并排序
for( int t = 0; t <= xx; t++ )
{
d = 1 << t;//向左移位,d的值分别是1,2,4,8,...
int newLen = int( len / ( 2*d ) ) * 2 * d;
//对长度是2d的偶数倍长度内的数据使用多趟归并排序
for( k = 0; k < newLen; k += 2*d )
{
Merge( arr, b, d, d, k );//一趟归并排序
}
//处理有尾巴的情形
int tail = len % (2*d);
if( tail != 0 )
{
if( tail <= d )
{
for( n = newLen; n < len; n++ )
{
b[n] = arr[n];
}
}
else if( tail > d )
{
Merge( arr, b, d, tail - d, newLen );
}
}
for( n = 0; n < len; n++ )
{
arr[n] = b[n];
}
//为方便观察排序结果,向屏幕输出每趟排序结果
printf( " No. %d time sort: ", t+1 );
for( n = 0; n < len; n++ )
{
printf( "%5d", arr[n] );
}
printf( "\n" );
}
delete[] b;
}
3.完整的代码
#include "stdio.h"
#include"math.h"
void MergeSort( int arr[], int len );
void Merge( int a[], int b[], int m, int n, int start );
int main()
{
int i;
int arr[] = { 3, 1, 5, 6, 7, 4, 2 };
int len = 7;
printf( " Initial Array: " );
for( i = 0; i < len; i++ )
{
printf( "%5d", arr[i] );
}
printf( "\n" );
MergeSort( arr, len );
return 0;
}
//对数组a从下标start到start+m-1的元素与从start+m到start+m+n-1归并排序并存储到数组b从start到start+m+n-1位置
void Merge( int a[], int b[], int m, int n, int start )
{
int i, j, k;
i = start;
j = start + m;
k = start;
while( i < start + m && j < start + m + n )
{
if( a[i] < a[j] )
{
b[k++] = a[i++];
}
else
{
b[k++] = a[j++];
}
}
while( i < start + m )
{
b[k++] = a[i++];
}
while( j < start + m + n )
{
b[k++] = a[j++];
}
}
//对长度为len的数组arr使用归并排序算法进行排序
//该方法使用了和arr相同长度的静态数组作为缓存
void MergeSort( int arr[], int len )
{
int k, n, m, x, xx;
unsigned int d;
x = int ( log(len) / log(2) );
int *b = new int[len];//缓存
//获取排序的趟数
if( int( pow( 2, x ) ) == len )
{
xx = x - 1;
}
else
{
xx = x;
}
//根据事先计算的趟数进行归并排序
for( int t = 0; t <= xx; t++ )
{
d = 1 << t;//向左移位,d的值分别是1,2,4,8,...
int newLen = int( len / ( 2*d ) ) * 2 * d;
//对长度是2d的偶数倍长度内的数据使用多趟归并排序
for( k = 0; k < newLen; k += 2*d )
{
Merge( arr, b, d, d, k );//一趟归并排序
}
//处理有尾巴的情形
int tail = len % (2*d);
if( tail != 0 )
{
if( tail <= d )
{
for( n = newLen; n < len; n++ )
{
b[n] = arr[n];
}
}
else if( tail > d )
{
Merge( arr, b, d, tail - d, newLen );
}
}
for( n = 0; n < len; n++ )
{
arr[n] = b[n];
}
//为方便观察排序结果,向屏幕输出每趟排序结果
printf( " No. %d time sort: ", t+1 );
for( n = 0; n < len; n++ )
{
printf( "%5d", arr[n] );
}
printf( "\n" );
}
delete[] b;
}
4.测试用例
测试用例一

测试用例二
测试用例三

测试用例四
