代码随想录算法训练营 Day2 | 数组 | LC.977、LC.209、LC.59
977. 有序数组的平方
题目描述
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序
双指针
class Solution {
public int[] sortedSquares(int[] nums) {
int len = nums.length;
int low = 0;
int high = len -1;
int[] res = new int[len];
int index = len - 1;
while(low < high){
if(Math.abs(nums[low]) <= Math.abs(nums[high])){
res[index--] = nums[high] * nums[high];
res[index--] = nums[low] * nums[low];
}else{
res[index--] = nums[low] * nums[low];
res[index--] = nums[high] * nums[high];
}
low++;
high--;
}
if(nums.length % 2 != 0){
res[index] = nums[low] * nums[high];
}
return res;
}
}
209. 长度最小的子数组
题目描述:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
滑动窗口,感觉好多这种类似描述的题,我一开始还以为用dp
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int len = nums.length;
int i = 0;
int j = 0;
int sum = 0;
int min = Integer.MAX_VALUE;
int subLen = 0;
for ( j = 0; j < len; j ++){
sum += nums[j];
while(sum >= target){
subLen = j - i + 1;
min = Math.min(min,subLen);
sum -= nums[i++];
}
}
return min == Integer.MAX_VALUE ? 0 : min;
}
}
59. 螺旋矩阵 II
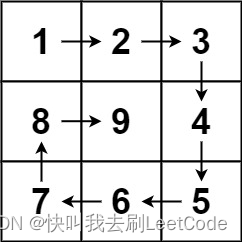
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
1 <= n <= 20
我太菜了,想了十几分钟的思路,然后整整花了两个多小时去debug,期间一直数组越界,
虽然耗时又长,写的代码也很复杂,折腾了很久,但是当自己不看任何题解以及提示把这题AC了后,是真的很开心很有成就感!
class Solution {
/*
有两种情况可能需要转弯
1.碰到边界的时候
2,原本移动的方向下一个位置已经被flag标记过了
停止循环移动的条件:
移动到下一个位置后发现该位置已经被标记过了,说明这个二维数组已经被赋值完了,此时把stop赋值为1
每次移动的时候会判断stop变量,如果stop为1则不移动了。
*/
int num = 0;
int stop = 0;
public int[][] generateMatrix(int n) {
if (n == 1) return new int[][]{{1}};
int[][] res = new int[n][n];
int[][] flag = new int[n][n];
moveRight(res, flag, 0, 0, n);
return res;
}
public void moveRight(int res[][], int flag[][], int y, int x, int n) {
if (flag[y][x] == 1) {
stop = 1;
}
x--;//先减一次,防止退出循环时数组越界
while (x < n - 1) {
x++;
if (flag[y][x] == 1 && stop == 0) { //循环过程中如果下一个位置是已经标记过了的,那么就转弯
//向下移动即y+1, 之所以要x-1是因为本方法是向右移动。
// 这一步判断了该位置即将右移的那个位置是否被标记了,如果是的话就要向下移动,而向下移动前需要先往左回退一次。
moveDown(res, flag, y + 1, x - 1, n);
}
if (flag[y][x] == 0) {
res[y][x] = ++num;
flag[y][x] = 1;
}
}
//这里还要判断一次是因为循环结束碰到边界了也要转弯。
if (flag[y][x] == 1 && stop == 0) {
moveDown(res, flag, y + 1, x, n);
}
}
public void moveDown(int res[][], int flag[][], int y, int x, int n) {
if (flag[y][x] == 1) {
stop = 1;
}
y--;
while (y < n - 1) {
y++;
if (flag[y][x] == 1 && stop == 0) {
moveLeft(res, flag, y - 1, x - 1, n);
}
if (flag[y][x] == 0) {
res[y][x] = ++num;
flag[y][x] = 1;
}
}
if (flag[y][x] == 1 && stop == 0) {
moveLeft(res, flag, y, x - 1, n);
}
}
public void moveLeft(int res[][], int flag[][], int y, int x, int n) {
if (flag[y][x] == 1) {
stop = 1;
}
x++;
while (x > 0) {
x--;
if (flag[y][x] == 1 && stop == 0) {
moveUp(res, flag, y - 1, x + 1, n);
}
if (flag[y][x] == 0) {
res[y][x] = ++num;
flag[y][x] = 1;
}
}
if (flag[y][x] == 1 && stop == 0) {
moveUp(res, flag, y - 1, x, n);
}
}
public void moveUp(int res[][], int flag[][], int y, int x, int n) {
if (flag[y][x] == 1) {
stop = 1;
}
y++;
while (y > 0) {
y--;
if (flag[y][x] == 1 && stop == 0) {
moveRight(res, flag, y + 1, x + 1, n);
}
if (flag[y][x] == 0) {
res[y][x] = ++num;
flag[y][x] = 1;
}
}
if (flag[y][x] == 1 && stop == 0) {
moveUp(res, flag, y - 1, x, n);
}
}
}