void InsertSort( SqList &L ) {
  int i,j;
  for (i=2; i<=L.length; ++i) {
    if (L.r[i].key < L.r[i-1].key){      //若"<" 需将L.r[i]插入有序子表
      L.r[0]=L.r[j];                     // 复制为哨兵
      for (j=i-1; L.r[0].key<L.r[j].key;-j){
          L.r[j+1]=L.r[];        // 记录后移
      }
       L.r[j+1]=L.r[0];        //插入到正确位置
  }
}

·性能分析：实现排序的基本操作为比较序列中关键字的大小和移动记录

1）空间效率：仅用了常数个辅助单元，空间复杂度为O(1)

2）时间效率：①最好情况表中的元素已经有序，每插入一个元素都只要比较一次，共比较n-1次，而且不用移动元素，移动次数为0，时间复杂度为O(n)；②最坏的情况表中元素顺序刚好和结果顺序相反即逆序，比较次数达到最大Σi=(n+2)(n-1)/2，移动次数也达到最大Σi+1=(n+4)(n-1)/2，时间复杂度为O(n2)；③平均情况下，可以取最好最坏情况的平均值，总比较和移动次数均约为n2/4，因此平均复杂度为O (n2)

·稳定性：每次插入元素总是从后向前先比较再移动，所以不会出现相同元素相对位置发生变化的情况，所以直接插入排序是稳定的排序方法

8.1.2 折半插入排序--采用折半查找插入位置

·基本过程：直接插入算法在插入过程中总是边比较边移动元素，而在折半插入中，比较和移动操作分离，即先折半查找出元素的待插入位置，然后统一的移动待插入位置之后的所有元素

·算法实现：

void InsertSort (ElemType A[],int n) {
  int i, j，low, high, mid; 
  for(i=2;i<=n;i++) {          //依次将A[2]~A[n]插入前面的已排序序列
    A[0]=A[i];                   //将A[i]暂存到A[0]
    1ow=1;high=i-1;              //设置折半查找的范围
    while (1ow<=high) {          //折半查找(默认递增有序)
      mid= (low+high)/2;          //取中间点
      if (A[mid]>A[0]) high=mid-1; //查找左半子表
      else low=mid+1;              //查找右半子表
      for(j=i-1;j>=high+1;--j)
        A[j+1]=A[j];                 //统一后移元素，空出插入位置
        A[high+1]=A[0];              //插入操作
    }
  }
}

·性能分析：由于折半查找比顺序查找快，所以就平均性能来说，折半插入比直接插入要快。在比较次数方面约为O(nlog2n)，它与待排序表的初始状态无关，仅取决于表中的元素个数n；在元素的移动次数方面和顺序插入相比并未改变，它依赖于待排序表的初始状态；

? 总的来说，折半插入减少了比较次数，没有减少移动次数，时间复杂度仍为O(n2)，空间复杂度为O(1)，是一种稳定的排序方法

8.1.3 希尔排序

?对于直接插入排序算法来说，若待排序列基本有序或者待排序列元素个数较少时，其效率可以得到很大的提高，基于这两点可以衍生出希尔排序

·基本思想：先将整个待排记录序列分割成若干子序列，分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

·基本过程：

1）定义增量序列Dk: Dm>Dm-1>...>D1=1，逐渐递减至1

2）对每个Dk进行"Dk间隔"插入排序(k=M, M-1, ..1)

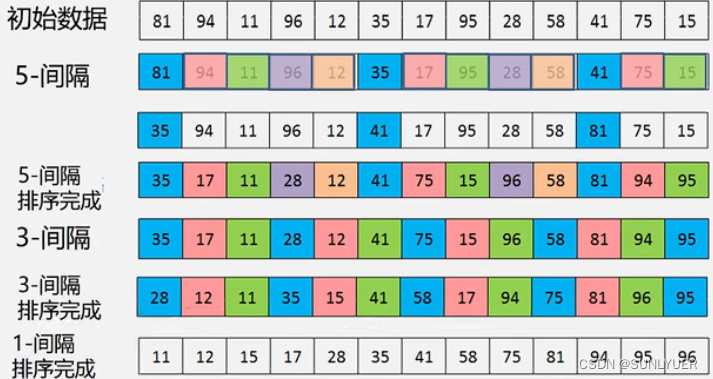
对下图所示元素，首先定义增量序列为5，对于5间隔（相同颜色）的元素进行插入排序，待5间隔的元素完成排序后，再设置比5小的增量序列进行相同的操作，最后到1时，只需要进行少量元素的移动

?·算法实现：

void ShellSort (ElemType AlIrint n){
//A[0]只是暂存单元，不是哨兵，当j<=0时，插入位置已到
  for (dk=n/2;dk>=1;dk=dk/2)        //步长变化 
    for(i=dk+1;i<=n;++i)
      if(A[i]<A[i-dk]){             //需将 A[i]插入有序增量子表
        A[0]=A[i];                  //暂存在A[0] 
        for(j=i-dk;j>0&&A[0]<A{j];j-=dk)
          A[j+dk]=A[j];             //记录后移， 查找插入的位置
        A[j+dk]=A[0];               //插入
      }//if
}

·算法效率：

1）空间效率：仅使用了常数个辅助单元，空间复杂度为O(1)

2）时间效率：希尔算法效率与增量序列的取值有关，当n在某个特定的范围内时，其时间复杂度为O(n1.25)，最坏情况下为O(n2)

·稳定性：当相同关键字的记录被划分到不同的子表时，可能会改变它们之间的相对次序，所以希尔排序是一种不稳定的排序方法

8.2 交换排序

8.2.1 冒泡排序

·基本思想：从前往后（或从后往前）两两比较相邻元素的值，若为逆序，则交换，直至比较完成，此为第一趟冒泡，结果是最小的元素“浮了上来”或者最大的元素“沉至水底”，

每一趟冒泡的结果就是把序列中的min 或max元素放到序列的最终位置，这样最多有n-1趟冒泡能把所有元素排好序，第i趟需要比较n-i次

?·算法实现：

void bubble_sort(SqList &L) {    //改进的冒泡排序算法
  int m,i,j,flag=1; RedType x;     //flag作为是否有交换的标记
  for(m=1; m<=n-1&&flag==1; m++) {
    flag=0; .
    for(j=1;j<=m;j++)
      if(L.rfi].key> L.r[j+1].key) { //发生逆序
      flag=1; //发生交换， flag置为1, 若本趟没发生交换，flag保持为0
      x=L.r[j];L.r[j]=L.r[j+ 1];L.r[j+1]=x; //交换
      } //endif
  }//for
}

·算法效率：

1）空间效率：仅使用了常数个辅助单元，空间复杂度为O(1)

2）时间效率：①最好情况当初始序列有序时，第一趟冒泡后直接跳出循环，一共进行比较n-1次，但是没有元素移动，时间复杂度为O(n)；②最坏情况初始序列逆序时，需要n-1趟排序，第i趟的需要比较n-i次，所以比较次数为Σn-i=n(n-1)/2，而后每次比较后都需要移动元素3次来进行交换所以移动次数为Σ3(n-i)=3n(n-1)/2，时间复杂度为O(n2)；

综上冒泡排序的平均复杂度为O(n2)，且是一种稳定的排序方法

8.2.2 快速排序

·基本思想：基于分治法，通过一趟排序，将待排序记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录进行排序，以达到整个序列有序

·基本过程：选定一个中间数作为参考，可以是第一个数也可以是最后一个数，所有元素与之比较，小的放左边，大的放右边，每一趟子表的形成采用从两头向中间交替式逼近法，然后分别递归地对这两个子表重复上述过程，直至每个部分只有一个元素或为空为止

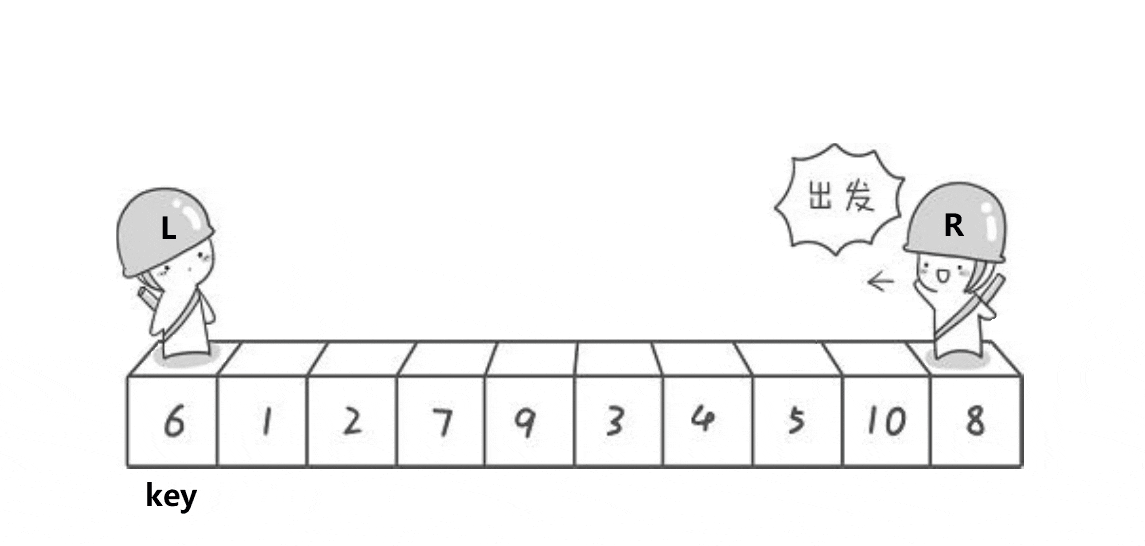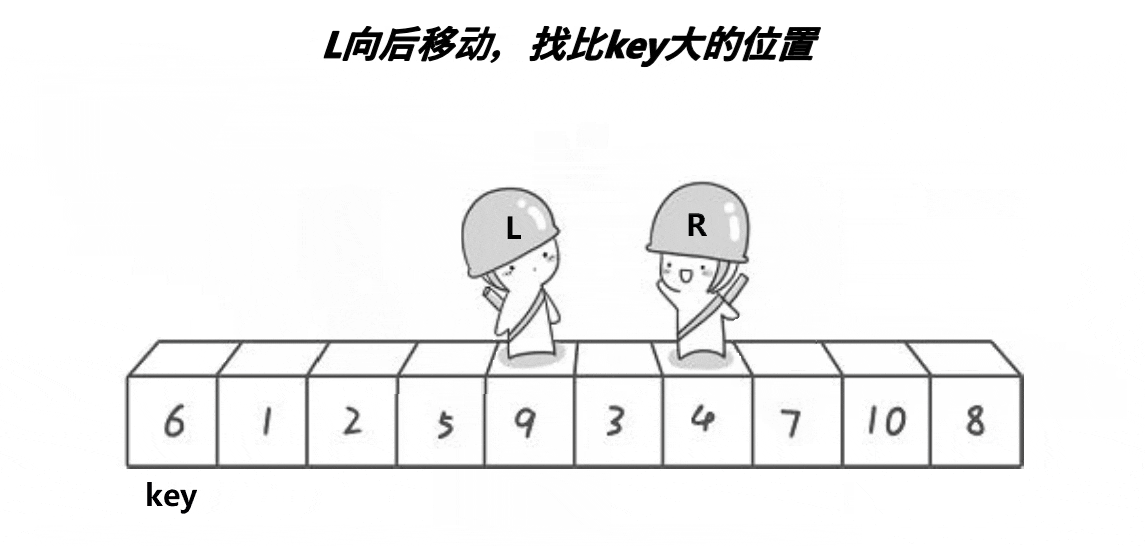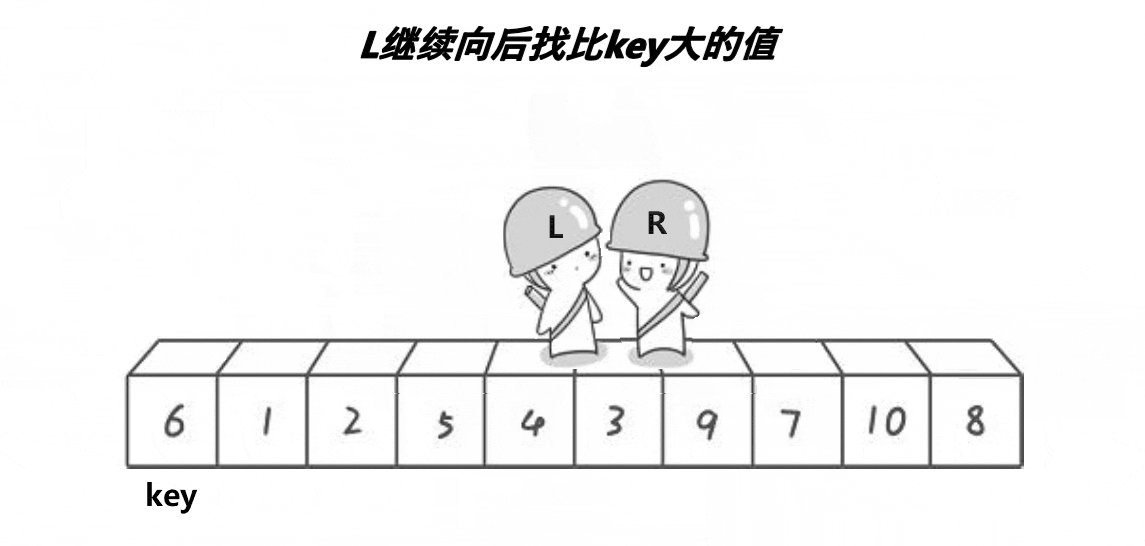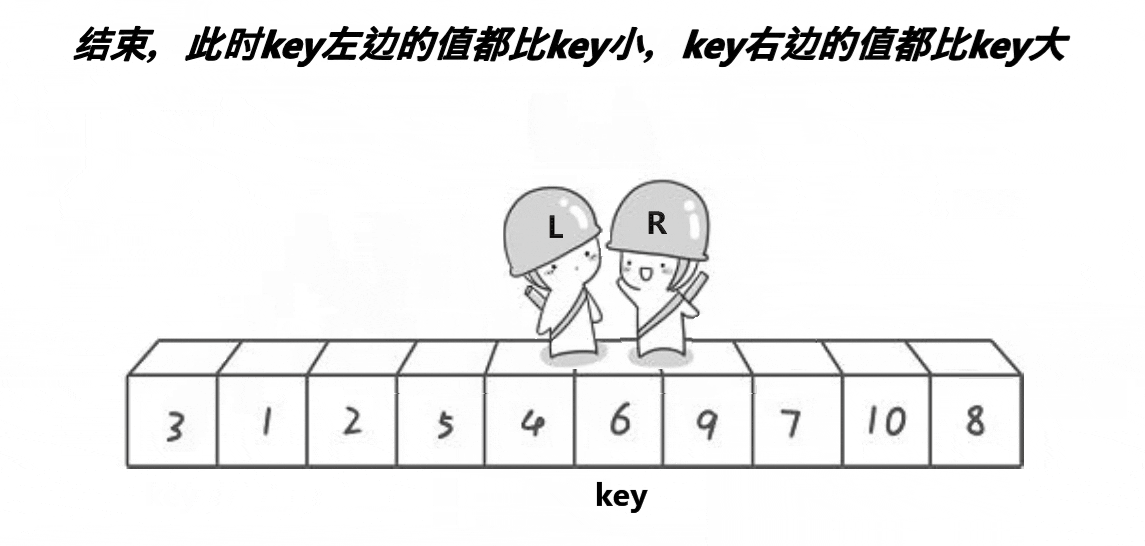
·算法实现：

快排算法：

void QuickSort (ElemType A[],int low,int high) {
  if (low<high) {            //递归跳出的条件
  //Partition()就是划分操作，将表A[low..high]划分为满足上述条件的两个子表
    int pivotpos=Partition(A, low,high);  //划分
    QuickSort (A，low,pivotpos-1);        //依次对两个子表进行 递归排序
    QuickSort (A, pivotpos+1,high);
  }
}

划分算法：

int Partition (ElemType A[], int 1ow, int high){ //一趟划分
  ElemType pivot=A[low];       //将当前表中第一个元素设为枢轴，对表进行划分
  while (low<high) {       //循环跳出条件
    while (low<high&&A[high]>-pivot) --high;
    A[low]=A[high];        //将比枢轴小的元素移动到左端
    while (low<high&&A[low]<=pivot) ++low;
    A[high]=A[low];        //将比枢轴大的元素移动到右端
  }
  A[low]=pivot;            //枢轴元素存放到最终位置
  return low;              //返回存放枢轴的最终位置
}

·算法效率：

1）空间效率：由于快排过程中使用了递归，需要递归调用栈的支持，而栈的长度取决于递归调用的深度，最好情况下为O(log2n); 最坏情况下，因为要进行n-1次递归调用，所以栈的深度为0(n);平均情况下，栈的深度为0(log2n)

2）时间效率：快排的运行时间与划分是否对称有关；①最坏情况发生在两个区域分别包含n-1和0个元素，这种最大程度的不对成性在每层的递归上，时间复杂度为O(n2)；②最好的情况下，即Partition()可能做到最平衡的划分，得到的两个子序列都不可能超过n/2，此时Partition()的时间复杂度为O(n)，而快排的时间复杂度为0(log2n)，所以平均时间复杂度为0(nlog2n)，在所有内部排序算法中平均性能最优

·稳定性：在划分算法中，若右端区间有两个关键字相同，且均小于基准值的记录，则在交换到左端区间后，它们的相对位置会发生变化，所以快排序是一种不稳定的排序方法。

【注】：划分元素的选取是影响时间性能的关键；输入数据次序越乱，所选划分元素值的随机性越好，排序速度越快，快速排序不是自然排序方法。

8.3 选择排序

8.3.1 简单选择排序

·基本思想：在待排序的数据中选取max or min 元素放在其最终的位置上

·基本过程：

1）通过n-1次关键字比较，从n个记录中找出关键字最小的记录，将它与第一个记录交换；

2）再通过n-2次比较，从剩余的n-1个记录中找出关键字次小的记录，将它与第二个记录交换；

3）重复上述操作，共进行n-1趟排序后，排序结束

·算法实现：

void SelectSort (ElemType A[],int n){
  for(i=0;i<n-1;i++){
    min=i ;
    for(j=i+1;j<n;j++)
      if(A[j]<A[min]) min=j;   //更新最小元素位置
    if (min!=i) swap(A[1],A[min]); //封装的swap()函数共移动元素3次
}

·算法效率：

1）空间效率：仅使用了常数个辅助单元，空间复杂度为O(1)

2）时间效率：最好情况下已经有序，移动次数为0，最坏情况下移动次数不超过3(n-1)；但元素的比较次数与序列的初始状态无关，始终是Σn-i=n(n-1)/2次，因此时间复杂度为O(n2)

·稳定性：在第i趟找到最小元素后，和第i个元素交换，可能会导致第i个元素与其含有相同关键字元素的相对位置发生改变。因此简单选择排序是一种不稳定排序

8.3.2 堆排序

·堆的定义：若n个元素的序列{a1 a2 .... an}满足：ai≤a2i 且ai≤a2i+1或ai≥a2i且ai≥a2i+1

则分别称该序列{a1 a2 ... an}为小根堆和大根堆。从定义上看，其本质就是一棵完全二叉树，树中任一非叶子结点均小于（大于）它的孩子结点

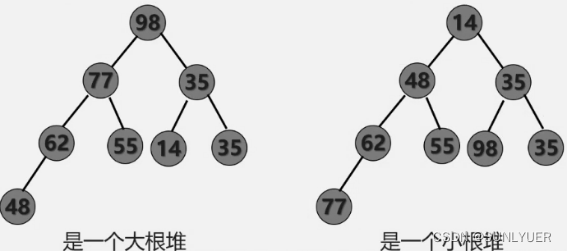
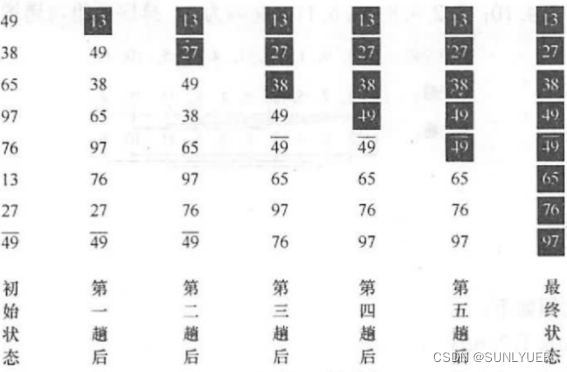
?·堆排序的思想：若在输出堆顶的最小值(最大值)后，使得剩余n- 1个元素的序列又建成一个堆，则得到n个元素的次小值(次大值) ....如此反复，便能得到一个有序序列，这个过程称为堆排序。这个过程主要需要解决两个问题：①如何将无序列构造成初始堆；②输出堆顶后如何将剩余元素调整为新的堆？

·堆的调整：

1）输出堆顶元素后，用堆中的最后一个元素代替它

2）将此时根结点的值与其左右子树的根结点比较，并与其中小者进行交换

3）重复上述比较直至叶子结点，这个堆顶到叶子结点的过程称为筛选

? ? 以上为小根堆的调整，大根堆找出大者进行交换即可

?·堆的构造：在完全二叉树中，所有以叶子结点(i>n/2)为根的子树为堆，即将序号为n/2，n/2 -1，..1的结点（从最后一个非叶子结点开始一直到根结点）为根的子树调整为堆

·算法实现：

?建堆

void HeapSort(int R[]){ //堆R[1]到R[p]进行堆排序
  int i;
  for(i= n/2;i>= 1;i--){
  HeapAdjust(R, i, n);  //建初始堆
  }
  for(i= n;i> 1;i--){   //进行n-1趟排序
    Swap(R[1], R[i]);   //根与最后一个元素交换
    HeapAdjust(R, 1, i-1); //对R[i]到R[i-1]重新建堆
  }
}

?调整堆

void HeapAdjust(elem R[]，int s, int m){
/*已知R[s.m]中 记录的关键字除R[s]之外均满足堆的定义，
  调整R[s]的关键字，使R[s. m]成为个大根堆*/
  rc= R[s]; 
  for (intj= 2*s;j<= m;j *= 2) {  //沿key较大的孩子节点向下筛选
    if(j< m && R[j] < R[j+1])     // j为key较大的记录的下标
      j++;
    if(re >= R[j])
      break;
    R[s]= R[j]; s=j;              //rc应插入在位置s上
  } 
  R[s]= rc;                       // rc应插入
}

·算法分析：

1）空间效率：仅使用了常数个辅助单元，空间复杂度为O(1)

2）时间效率：初始阶段建堆时间为O(n)，排序阶段每次重新堆化的时间不超过O(log2n)，在n-1次向下调整的过程时间复杂度就为O(nlog2n)，所以堆排序的时间复杂度为O(nlog2n)；

【注】：堆排序的时间主要耗费在建初始堆和调整建新堆时进行的反复“筛选”上。最坏情况下，其时间复杂度也为O(nlog2n),这是堆排序的最大优点。无论待排序列中记录是正序还是逆序排序，都不会使堆排序处于"最好”或“最坏”的状态。

·稳定性：在筛选的过程中，可能会把后面相同的关键字调整到前面，所以堆排序是不稳定的排序方法

8.4 归并与基数排序

8.4.1 归并排序

·基本思想：将两个或两个以上的有序子序列，归并为一个有序序列，在内部排序中，通常采用2路归并排序，即将两个位置上相邻的有序子序列归并（倒二叉树），共需O(log2n)趟

?·两个有序序列的合并：设两段有序表SR[low..mid]、SR[mid+1..high]存放在同一顺序表中的相邻位置，每次从两个段取出一个记录进行关键字的比较，将较小者放入TR中，当数组B中有一段的下标超出其对应的表长(即该段的所有元素都已复制到TR中)时，将另一段中的剩余部分直接复制到TR中

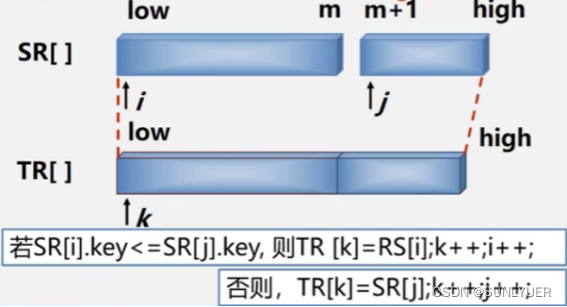
·算法分析：

1）空间效率：需要一个与原始序列同样大小的辅助序列，空间复杂度为O(n)

2）时间效率：每趟归并的时间复杂度为O(n)，共有O(log2n)趟归并，所以时间复杂度为O(nlog2n)，且相对次序稳定，是一种稳定的排序方法

8.4.2 基数排序

·基本思想：基数排序不基于比较和移动进行排序,而基于关键字各位的大小进行排序。是一种借助多关键字排序的思想对单逻辑关键字进行排序的方法。

·基本过程：

1）第一趟将个位相同的记录分配到同一队列中

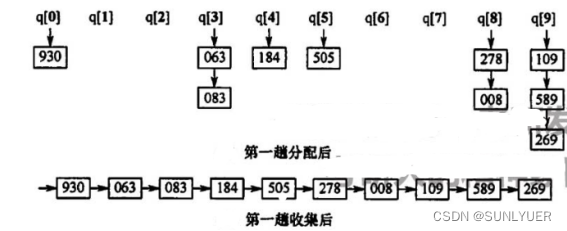
2）第二趟将十位相同的记录分配到同一队列

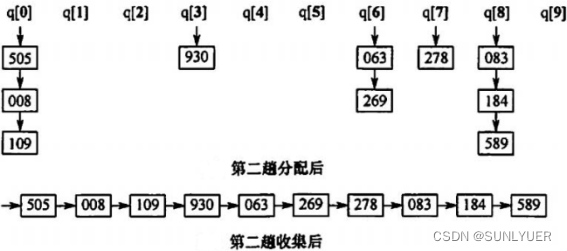
?3）第三趟将百位相同的记录分配到同一队列

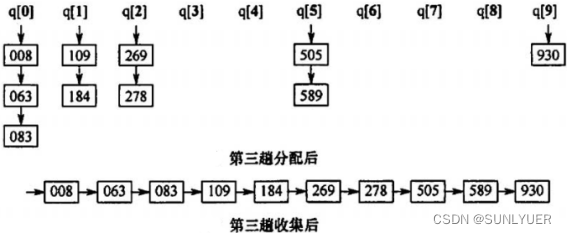
·效率分析：

1）空间效率：一趟排序需要的辅助存储空间为r (r个队列: r个队头指针和r个队尾指针)，但以后的排序中会重复使用这些队列，所以基数排序的空间复杂度为0(r)。

2）时间效率：基数排序需要进行d趟分配和收集，一趟分配需要 O(n)，-趟收集需要0(r),所以基数排序的时间复杂度为O(d(n + r))，它与序列的初始状态无关，且由于按位排序时必须是稳定的，保证了基数排序的稳定性

8.5 内部排序算法总结

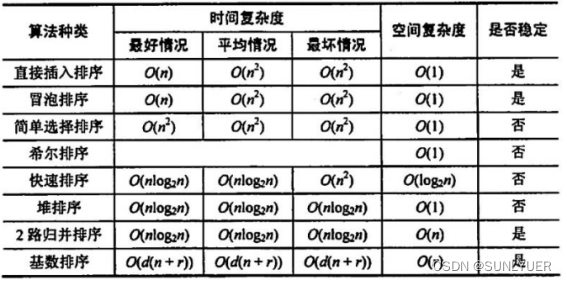
·选择算法考虑因素：

①待排序的元素数目n

②元素本身信息量的大小

③关键字的结构及其分布情况

④稳定性的要求。

⑤语言工具的条件，存储结构及辅助空间的大小等

·选择算法：

1）若n较小，可采用直接插入排序或简单选择排序。由于直接插入排序所需的记录移动次数较简单选择排序的多，因而当记录本身信息量较大时，用简单选择排序较好；

2）若n较大,则应采用时间复杂度为0(nlog2n)的排序方法:快速排序、堆排序或归并排序。快速排序被认为是目前基于比较的内部排序方法中最好的方法，当待排序的关键字随机分布时，快速排序的平均时间最短。堆排序所需的辅助空间少于快速排序，并且不会出现快速排序可能出现的最坏情况，这两种排序都是不稳定的。若要求排序稳定且时间复杂度为O(nlog2n),则可选用归并排序。但从单个记录起进行两两归并的排序算法并不值得提倡，通常可将它和直接插入排序结合在一起使用。先利用直接插入排序求得较长的有序子文件，然后两两归并。直接插入排序是稳定的，因此改进后的归并排序仍是稳定的；

3）若n很大，记录的关键字位数较少且可以分解时，采用基数排序较好；

4）若文件的初始状态已按关键字基本有序，则选用直接插入或冒泡排序为宜；

5）在基于比较的排序方法中，每次比较两个关键字的大小之后，仅出现两种可能的转移，因此可以用一棵二叉树来描述比较判定过程，由此可以证明:当文件的n个关键字随机分布时，任何借助于“比较”的排序算法，至少需要O(nlog2n)的时间。