目录
101. 对称二叉树 - 力扣(LeetCode)
给你一个二叉树的根节点?root?, 检查它是否轴对称。
思路:
这种检查树的对称性的情况,一般使用递归算法解决,设计好一层的轴对称检查方法,递归下去就可以。
首先新建两个指针p and q,都是指向root,p指向左移动p.left,q向右移动q.right,之后判断节点的值是否相同,若相同,判断p.right 和q.left。递归终止条件是p 或者q存在一个或者p 和q都为空。
(python and cpp)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def check(self,p:Optional[TreeNode],q:Optional[TreeNode]):
# 递归终止条件
if not (p or q):return True
if not (p and q):return False
return p.val == q.val and self.check(p.left,q.right) and self.check(p.right,q.left)
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
return self.check(root,root)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return check(root,root);
}
bool check(TreeNode* p,TreeNode* q){
if (!p && !q) return true;
if (!p || !q) return false;
return p->val == q->val && check(p->left,q->right) && check(p->right,q->left);
}
};104. 二叉树的最大深度 - 力扣(LeetCode)
给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
思路:
使用深度优先遍历,通过递归的方式寻找深度。
(python and c++)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if (!root) return 0;
return max(maxDepth(root->left),maxDepth(root->right)) + 1;
}
};# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
# DFS
if not root:return 0;
return max(self.maxDepth(root.left),self.maxDepth(root.right)) + 1
121. 买卖股票的最佳时机 - 力扣(LeetCode)
给定一个数组 prices ,它的第?i 个元素?prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0?
思路:
动态规划。定义dp[i]是第i天卖出股票时的利润,定义变量minprice = price[0],遍历时更新;则dp[i]=min(dp[i-1],dp[i]-minprice),初始值:dp[0]=0
(python? and? c++)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
# 动态规划
n = len(prices)
if not n: return 0
dp = [0] * n
minprice = prices[0]
dp[0] = 0
for i in range(1,n):
minprice = min(minprice,prices[i])
dp[i] = max(dp[i-1],prices[i]-minprice)
return dp[n-1]
class Solution {
public:
int maxProfit(vector<int>& prices) {
//dp
int n = prices.size();
if (n < 2) return 0;
int minprice = prices[0];
vector<int> dp(n,-1);
for (int i = 1;i < n;i++){
minprice = min(minprice,prices[i]);
dp[i] = max(dp[i-1],prices[i]-minprice);
}
return dp[n-1];
}
};136. 只出现一次的数字 - 力扣(LeetCode)
思路:
- 使用集合存储数字。遍历数组中的每个数字,如果集合中没有该数字,则将该数字加入集合,如果集合中已经有该数字,则将该数字从集合中删除,最后剩下的数字就是只出现一次的数字。
- 使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数,并更新哈希表,最后遍历哈希表,得到只出现一次的数字。
- 使用集合存储数组中出现的所有数字,并计算数组中的元素之和。由于集合保证元素无重复,因此计算集合中的所有元素之和的两倍,即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次,其余元素都出现两次,因此用集合中的元素之和的两倍减去数组中的元素之和,剩下的数就是数组中只出现一次的数字。
- 使用异或
使用1,2,3方法的空间复杂度都是o(n),使用异或的空间复杂度是O(1);
异或的三个性质:

?这个使用第1条和第3条性质;给定初始值0,遍历数组做异或运算,根据第3条性质,可以得出最后剩下的就是出现一次的元素。
(c++ and Python)
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res = 0;
for(auto& num:nums) res ^= num;
return res;
}
};?python 中使用lambda关键字。reduce函数和lambda关键字结合:此时lambda函数用于指定列表中两两相邻元素的结合条件。
class Solution:
def singleNumber(self, nums: List[int]) -> int:
# 调用rudece 函数;使用lambda关键字定义异或运算函数
return reduce(lambda x,y:x^y,nums)141. 环形链表 - 力扣(LeetCode)
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递?。仅仅是为了标识链表的实际情况。
如果链表中存在环?,则返回 true 。 否则,返回 false?
思路:
方法1:使用快慢指针,判别链表是否闭合(有环)。
定义一个快指针fast = head.next 和一个慢指针slow = head,while循环,当fast == slow 为true,则链表中有环。
(python and c++)
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
if not head or not head.next:return False
fast,slow = head.next,head
while fast != slow:
if not (fast and fast.next):return False
fast = fast.next.next
slow = slow.next
return True
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
if (head == nullptr || head->next == nullptr) return false;
ListNode* fast = head->next->next,*slow = head->next;
while (fast != slow){
if (fast == nullptr || fast->next == nullptr) return false;
fast = fast->next->next;
slow = slow->next;
}
return true;
}
};方法2:遍历所有节点,将遍历过的节点保存在哈希表中,每次都要判断该节点是否遍历过,若重复遍历,则肯定是有环。
(c++? and python)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
if (head == nullptr || head->next == nullptr) return false;
unordered_set<ListNode*> seen;
while (head != nullptr){
if (seen.find(head) != seen.end()){
return true;
}
seen.emplace(head);
head = head->next;
}
return false;
}
};# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
if not head or not head.next: return False
seen = set()
while head:
if head in seen:
return True
seen.add(head)
head = head.next
return False
160. 相交链表 - 力扣(LeetCode)
给你两个单链表的头节点?headA?和?headB?,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回?null?。
?思路:
方法1:将一个链表的所有节点放到哈希表中,遍历另一个链表,判断,若节点在哈希表中,则该节点为相交节点,若不是,继续遍历。
(python and c++)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
unordered_set<ListNode*> seen;
while (headA){
seen.insert(headA);
headA = headA->next;
}
while (headB){
if (seen.count(headB)) return headB;
headB = headB->next;
}
return nullptr;
}
};# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
seen = set()
while headA:
seen.add(headA)
headA = headA.next
while headB:
if headB in seen:
return headB
headB = headB.next
return None方法2:双指针。
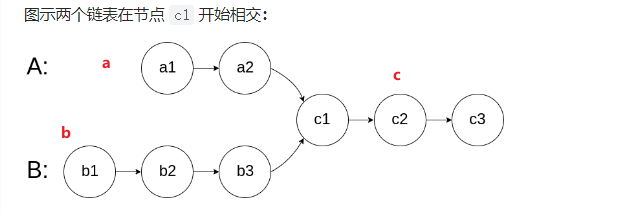
?假设:headA 的不相交部分的节点个数是a,headB 的不想交节点个数是b,相交的节点个数是c个。新建pA指针指向A头结点,pB指针指向B头结点,两个指针每次都移动一个节点,若:
a = c,则两个指针同时到达c1节点,pA = pB;
a != c, 则遍历一次链表pA 和pB 是不会相交的,走到c3时,pA 走过的距离:a + c;pB 走过的距离:b + c; 此时:让pA 指向headB,pB 指向headA,则他们在c1点相遇时,pA 走过的距离:a+c+b;pB 走过的距离: b+c+a。
(python and c++)
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
if not headA or not headB:return None
pa = headA
pb = headB
while pa != pb:
pa = pa.next if pa else headB
pb = pb.next if pb else headA
return pa/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (headA == nullptr or headB == nullptr) return nullptr;
ListNode* pa = headA,*pb = headB;
while (pa != pb){
pa = pa == nullptr ? headB : pa->next;
pb = pb == nullptr ? headA : pb->next;
}
return pa;
}
};