[数据结构与算法]leetcode 53. 最大子数组和-java实现

题目所属分类

简单的DP
复杂的分治思路

原题链接

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

代码案例：输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

题解

简单DP方法O(n)

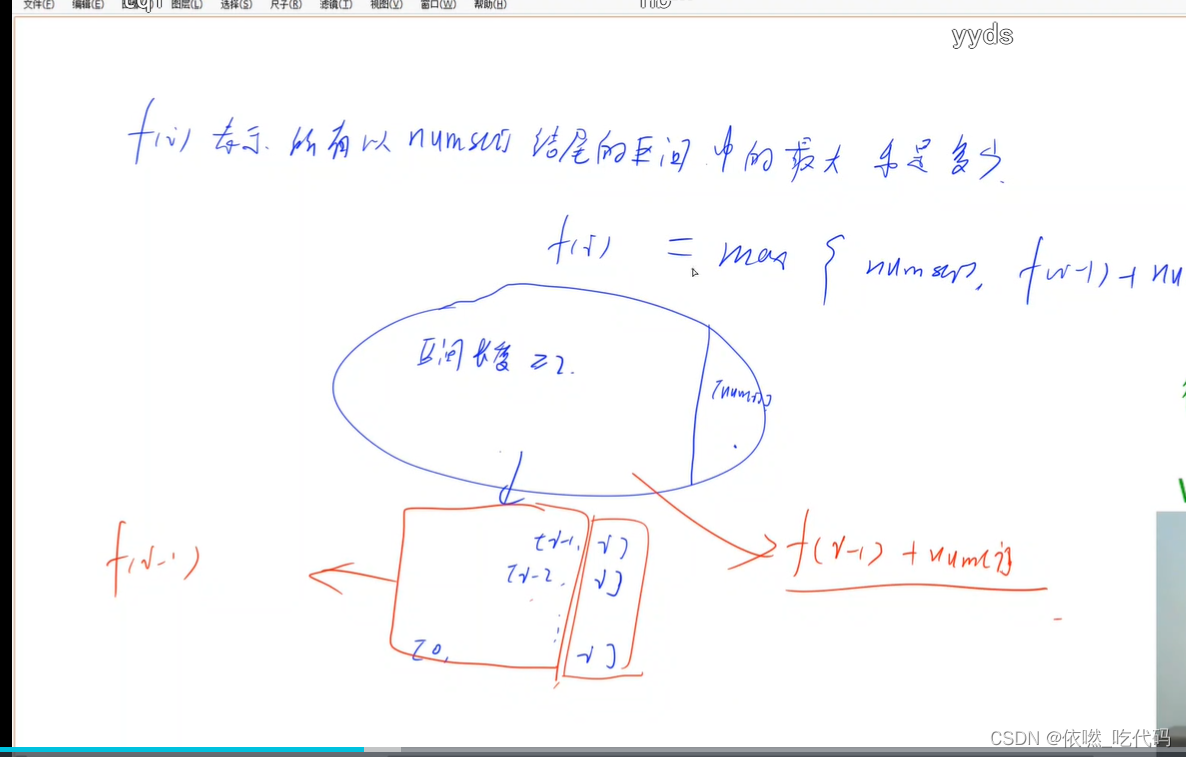
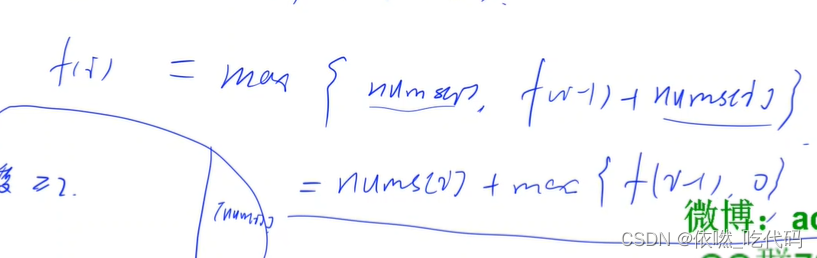
f[i]表示所有以nums[i]结尾的最大值

 class Solution {
    public int maxSubArray(int[] f) {
        //可以用last表示f[i-1]
            int ans = f[0] ; 
            int n = f.length ;
            for(int i = 0,last = 0 ; i < n ; i ++){              
                 last = Math.max(last,0) + f[i];
                ans = Math.max(ans,last);
            }
            return ans ;
    }
}

分治法O(nlogn)

1、以中点为中心向左遍历求出leftMax,向右遍历求出rightMax,则该区域的ans = lMax + rMax - nums[mid] (中点位置重复累加)

2、使用分治求出左区域【start，mid - 1】的最大值leftMax

3、使用分治求出右区域【mid + 1，end】的最大值rightMax

4、求Max(ans,leftMax,rightMax)
不过这个start大于end要是没有的话 就会显示栈溢出 所以要加这么一个判定

class Solution {
    public int maxSubArray(int[] nums) {
        return f(nums,0 , nums.length - 1);
    }
    public int f(int[] a,int start,int end){
        if(start > end) return Integer.MIN_VALUE;
        if(start ==  end ) return  a[start];
        int mid = (start + end) >> 1 ;
        int lmax = a[mid] , lsum = 0 , rmax = a[mid] , rsum = 0 ;
        for(int i = mid ; i >= start ; i -- ){
            lsum += a[i];
            lmax = Math.max(lmax,lsum);
        }
         for(int i = mid ; i <= end ; i ++ ){
            rsum += a[i];
            rmax = Math.max(rmax,rsum);
        }
        int ans = lmax + rmax -a[mid];   
       int leftMax =  f(a,start,mid - 1 );
        int rightMax = f(a,mid + 1,end );
        return  Math.max(Math.max(leftMax,rightMax),ans);
    }
}