[数据结构与算法]LeetCode-96-不同的二叉搜索树

1、动态规划法

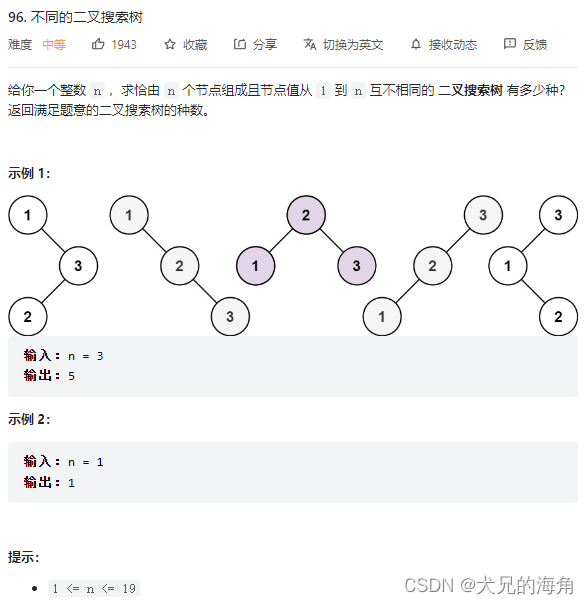
我们用数组$dp[n]$记录当节点数为$n$时，互不相同的二叉搜索树的个数。我们不难发现数组$dp$有这样的规律。当有$n$个节点构成的二叉搜索树时，我们可以假设节点$1$到$n$依次作为整棵树的根节点，此时会出现不同的情况：1、当1作为根节点时，其他所有节点都在根节点的右侧，故根节点左子树有0个节点，右子树有$n?1$个节点，此时可能的二叉搜索树个数有$dp[0]?dp[n?1]$个情况；2、当2作为根节点时，除了1之外的所有节点都在根节点的右子树，1在根节点的左子树，此时可能的二叉搜索树个数有$dp[1]?dp[n?2]$个情况…此时不难看出，我们想要求解$dp[n]$的值，就需要遍历从$dp[0]?dp[n?1]+dp[1]?dp[n?2]+...+dp[n?1]?dp[0]$的所有情况。

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1, 0);
        dp[0] = dp[1] = 1;
        for (int i = 2; i < n + 1; ++i) {
            for (int j = 0; j < i; ++j) {
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }
};

2、数学

$dp[n]$中的值就是数学上的卡塔兰数$C_n$，定义为：$$C_0=1,C_{n+1}=\frac{2(2n+1)}{n+2}{C}_n$$

class Solution {
public:
    int numTrees(int n) {
        long long C = 1;
        for (int i = 0; i < n; ++i) {
            C = C * 2 * (2 * i + 1) / (i + 2);
        }
        return (int)C;
    }
};