1、已知一棵有2011个结点的树,其叶结点个数为116,该树对应的二叉树中无右孩子的结点个数是()。
- A:115
- B:116
- C:1895
- D:1896
解析
树转换为二叉树时,树的每个分支结点的所有子结点中的最右子结点无右孩子,根结点转换后也没有右孩子,因此,对应二叉树中无右孩子的结点个数=分支结点数+1=2011-116+1=1896。
答案:D
2、将森林F转换为对应的二叉树T,F中叶结点的个数等于()。
- A:T中叶结点的个数
- B:T中度为1的结点个数
- C:T中左孩子指针为空的结点个数
- D:T中右孩子指针为空的结点个数
解析
答案:C
3、给定整数集合{3,5,6,9,12},与之对应的哈夫曼树是()。
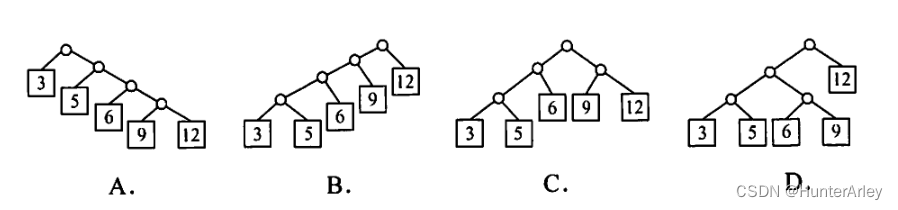
解析
首先,3和5构造为一棵子树,其根权值为8,然后该子树与6构造为一棵新子树,根权值为14,再后9与12构造为一棵子树,最后两棵子树共同构造为一棵哈夫曼树。
答案:C
4、设哈夫曼编码的长度不超过4,若已对两个字符编码为1和01,则最多可对()个字符编码。
- A:2
- B:3
- C:4
- D:5
解析
在哈夫曼编码中,一个编码不能是任何其他编码的前缀。3位编码可能是001,对应的4位编码只能是0000和0001。3位编码也可能是000,对应的4位编码只能是0010和0011.若全采用4位编码,则可以位0000,0001,0010和0011.题中问的是最多,所以选C。
答案:C
5、一棵哈夫曼树共有215个结点,对其进行哈夫曼编码,共能得到()个不同的码字。
- A:107
- B:108
- C:214
- D:215
解析
在哈夫曼树中只有度为0和度为2的结点,结点总数n= n 0 n_0 n0?+ n 2 n_2 n2?,且 n 0 n_0 n0?= n 2 n_2 n2?+1,题中n=215,所以 n 0 n_0 n0?=108
答案:B
6、以下对于哈夫曼树的说法中,错误的是:
- A :对应一组权值构造出来的哈夫曼树一般不是唯一的
- B:哈夫曼树具有最小的带权路径长度
- C:哈夫曼树中没有度为1的结点
- D:哈夫曼树中除了度为1的结点外,还有度为2的结点和叶结点
解析
哈夫曼树通常是指带权路径长度达到最小的扩充二叉树,在其构造过程中每次选根的权值最小的两棵树,一棵作为左子树,一棵作为右子树,生成新的二叉树,新的二叉树根的权值应为其左右两棵子树根结点权值的和。对哪棵子树做左子树还是右子树没有限制,所以构造的哈夫曼树是不唯一的。哈夫曼树只有度为0和度为2的结点,度为0的结点是外结点,带有权值,没有度为1的结点。
答案:D
7、并查集中最核心的两个操作:1.查找,查找两个元素是否属于同一个集合;2.合并,如果两个元素不属于同一个集合,且所在的两个集合互不相交,则合并这两个集合。假设初始长度为10(0~9)的并查集,按1-2、3-4、5-6、7-8、8-9、1-8、0-5、1-9的顺序进行查找和合并操作,最终并查集共有()个集合。
- A:1
- B:2
- C:3
- D:4
解析
初始时,0~9各自成一个集合。查找1-2时,合并{1}和{2};查找3-4时,合并{3}和{4};查找5-6时,合并{5}和{6};查找7-8时,合并{7}和{8};查找8-9时,合并{7,8}和{9};查找1-8时,合并{1,2}和{7,8,9};查找0-5时,合并{0}和{5,6};查找1-9时,它们属于同一个集合。最终的集合为{0,5,6}、{1,2,7,8,9}和{3,4},因此答案选C。
答案:C
8、下列关于并查集的叙述中,()是错误的(注意,本题涉及图的考点)。
- A:并查集是用双亲表示法存储的树
- B:并查集可用于实现克鲁斯卡尔算法
- C:并查集可用于判断无向图的连通性
- D:在长度为n的并查集中进行查找操作的时间复杂度为O( l o g 2 n log_2n log2?n)
解析
在用并查集实现Kruskal算法求图的最小生成树时:判断是否加入一条边之前,先查找这条边关联的两个顶点是否属于同一个集合(即判断加入这条边之后是否形成回路),若形成回路,则继续判断下一条边;若不形成回路,则将该边和边对应的顶点加入最小生成树T,并继续判断下一条边,直到所有顶点都已加入最小生成树T。B正确。
用并查集判断无向图连通性的方法:遍历无向图的边,每遍历到一条边,就把这条边连接的两个顶点合并到同一个集合中,处理完所有边后,只要是相互连通的顶点都会被合并到同一个子集合中,相互不连通的顶点一定在不同的子集合中。C正确。
未做路径优化的并查集在最坏的情况下的高度为O(n),此时查找操作的时间复杂度为O(n),时间复杂度通常指最坏情况下的时间复杂度。D错误。
答案:D
9、下列选项给出的是从根分别到达两个叶结点路径上的权值序列,属于同一棵哈夫曼树的是()。
- A:24,10,5和24,10,7
- B:24,10,5和24,12,7
- C:24,10,10和24,14,11
- D:24,10,5和24,14,6
解析
答案:D
10、对n个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有115个结点,则n的值是()。
- A:56
- B:57
- C:58
- D:60
解析
n个符号构造成哈夫曼树的过程中,共新建了n-1个结点(双分支结点),因此哈夫曼树的结点总数为2n-1=115,n的值为58,答案选C。